Comment implémenter la sommation en Java sans opérateurs arithmétiques

La question dit que les opérateurs arithmétiques ne peuvent pas être utilisés, nous ne pouvons donc commencer qu'avec des opérateurs logiques et des opérateurs de décalage.

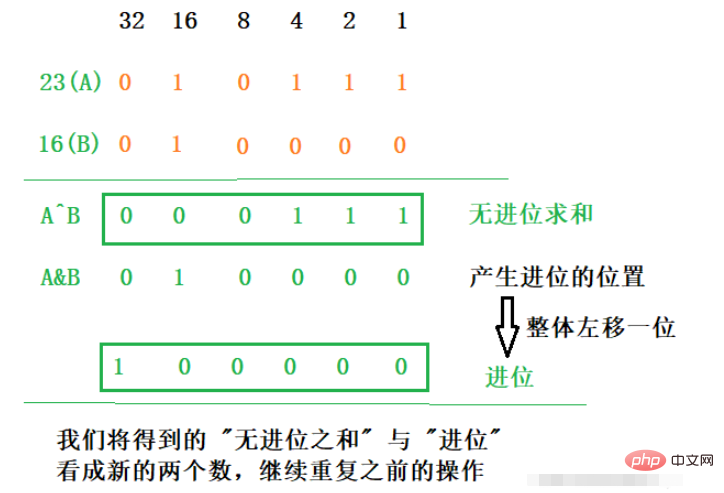
Nous savons que l'opération ^ (XOR) est une somme sans retenue de deux nombres. Si l'addition de deux nombres ne produit pas de retenue, alors la somme est la somme des deux nombres. C’est la clé pour résoudre le problème. D'une manière générale, l'addition de deux nombres produira un report. Pour obtenir la somme correcte, nous devons ajouter un report sur la base de la « somme sans report ». Ensuite, nous devons d'abord obtenir le report. Nous savons que lorsque les positions correspondantes des deux nombres sont toutes deux 1, une retenue se produira, c'est-à-dire que, à condition que les positions correspondantes A&B==1, nous pouvons obtenir une retenue pour chaque bit, mais la retenue doit être additionnée. ce 1 au chiffre supérieur correspondant, on décale donc le report obtenu vers la gauche d'un chiffre, puis on l'ajoute à la "somme sans report" obtenue précédemment, pour obtenir la somme des deux nombres.

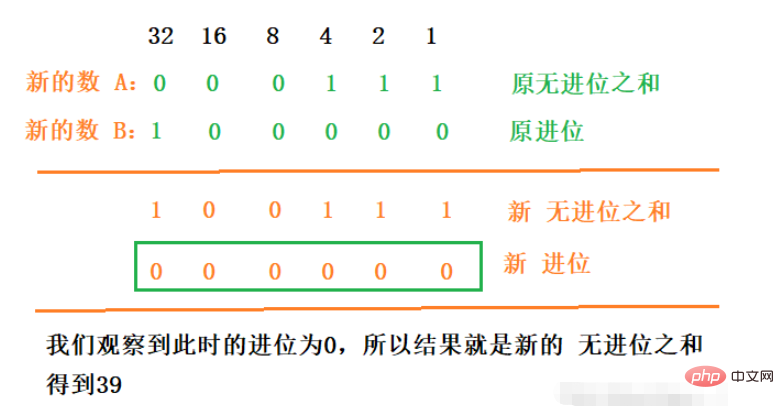
Nous constatons que nous pouvons créer ici des poupées matriochka infinies. Pour obtenir la somme de la « somme sans report » et du « report généré », traitez ensuite ces deux nombres comme deux nouveaux nombres respectivement et additionnez-les. L'opération précédente est également répétée jusqu'à ce que les deux nombres ne puissent pas produire de report, et le résultat peut être obtenu directement via l'opération ^.

Supposons que nous trouvions la valeur de 23 + 16

Selon les idées ci-dessus, nous pouvons facilement écrire le code

public static int addAB(int A, int B) {
		// 当两数的产生的进位为 0,就退出循环，返回其无进位和，就是结果
        while ((A & B) != 0) {
            int A_B = A ^ B;// 无进位求和
            int AB = (A & B) << 1;// 得到进位
            // 接下来就是求 得到的进位 + 无进位之和，重复前面的操作，直到不产生进位
            A = A_B;
            B = AB;
        }
        // 最后返回新的无进位之和
        return (A ^ B);
    }

Donc, afin de vérifier son exactitude, nous utilisons ici un logarithmiseur et convertissons le Les fonctions sont comparées à l'opérateur ’

public static void main(String[] args) {
    int count = 1_0000_0000;// 比较次数 100000000次
    Random random = new Random();// 生成随机数字
    boolean flag = true;// 相等则为 true

    for (int i = 0; i < count; i++) {
        int num1 = random.nextInt(Integer.MAX_VALUE/2);// 随机正数1
        int num1_2 = random.nextInt(Integer.MAX_VALUE/2);// 随机正数2
        // 随机正数1 + 随机正数2
        if ((num1+num1_2) != addAB(num1,num1_2)){
            // 有一次不相等的，则退出循环
            flag = false;
            break;
        }

        int num2 = -random.nextInt(Integer.MAX_VALUE/2);// 随机负数1
        int num2_2 = -random.nextInt(Integer.MAX_VALUE/2);// 随机负数2
        // 随机负数1  + 随机负数2
        if ((num2+num2_2) != addAB(num2,num2_2)){
            // 有一次不相等的，则退出循环
            flag = false;
            break;
        }

        int num3 = random.nextInt(Integer.MAX_VALUE);// 随机正数
        int num4 = -random.nextInt(Integer.MAX_VALUE);// 随机负数
        // 随机正数  + 随机负数
        if ((num3+num4) != addAB(num3,num4)){
            // 有一次不相等的，则退出循环
            flag = false;
            break;
        }
    }
    System.out.println(flag);
}

Résultats d'exécution :

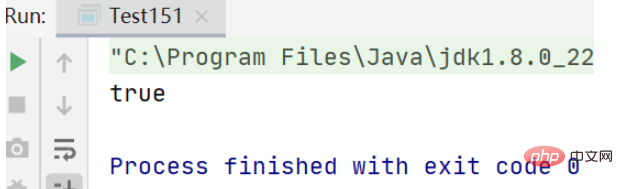
Le résultat final est vrai, ce qui signifie que nous avons calculé les nombres positifs + nombres positifs générés aléatoirement, les nombres négatifs + nombres négatifs, les nombres positifs + nombres négatifs 100 000 000 de fois respectivement, sans aucune erreur. , indiquant que la fonction est fiable.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!