Idée :
Puisqu'il s'agit d'un tableau ordonné, vous pouvez d'abord obtenir la position médiane, et le point médian peut diviser le tableau en gauche et les moitiés droites.
Si la valeur de la position médiane est égale à la valeur cible, renvoyez directement la position médiane.
Si la valeur de la position médiane est inférieure à la valeur cible, allez sur le côté gauche du point médian du tableau et recherchez de la même manière.
Si la valeur de la position médiane est supérieure à la valeur cible, prenez le côté droit du point médian du tableau et recherchez de la même manière.
Si vous n'êtes pas trouvé au final, retournez : -1.
Code
class Solution {
public int search(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
return m;
} else if (arr[m] > t) {
r = m - 1;
} else {
l = m + 1;
}
}
return -1;
}
}Complexité temporelle O(logN). O(logN)。
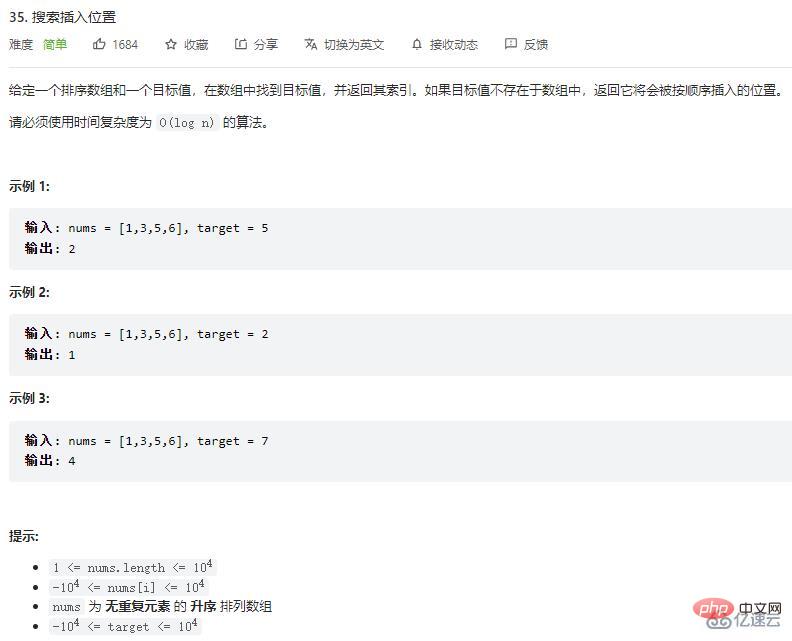
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
说明：如果要在num这个数组中插入 5 这个元素，应该是插入在元素 3 和 元素 5 之间的位置，即 2 号位置。
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
说明：如果要在num这个数组中插入 2 这个元素，应该是插入在元素 1 和 元素 3 之间的位置，即 1 号位置。
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
说明：如果要在num这个数组中插入 7 这个元素，应该是插入在数组末尾，即 4 号位置。
通过上述示例可以知道，这题本质上就是求在一个有序数组中，找大于等于某个数最左侧的位置，如果不存在，就返回数组长度（表示插入在最末尾位置）
我们只需要在上例基础上进行简单改动即可，上例中，我们找到满足条件的位置就直接return了
if (arr[m] == t) {
return m;
}在本问题中，因为要找到最左侧的位置，所以，在遇到相等的时候，只需要先把位置记录下来，不用直接返回，然后继续去左侧找是否还有满足条件的更左边的位置。
同时，在遇到arr[m] > t条件下，也需要记录下此时的m位置，因为这也可能是满足条件的位置。
代码：
class Solution {
public static int searchInsert(int[] arr, int t) {
int ans = arr.length;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l)>>1);
if (arr[m] >= t) {
ans = m;
r = m - 1;
} else {
l = m + 1;
}
}
return ans;
}
}整个算法的时间复杂度是O(logN)。
思路
本题也是用二分来解，当通过二分找到某个元素的时候，不急着返回，而是继续往左（右）找，看能否找到更左（右）位置匹配的值。
代码如下：
class Solution {
public static int[] searchRange(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return new int[]{-1, -1};
}
return new int[]{left(arr,t),right(arr,t)};
}
public static int left(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int ans = -1;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
ans = m;
r = m - 1;
} else if (arr[m] < t) {
l = m +1;
} else {
// arr[m] > t
r = m - 1;
}
}
return ans;
}
public static int right(int[] arr, int t) {
if (arr == null || arr.length < 1) {
return -1;
}
int ans = -1;
int l = 0;
int r = arr.length - 1;
while (l <= r) {
int m = l + ((r - l) >> 1);
if (arr[m] == t) {
ans = m;
l = m + 1;
} else if (arr[m] < t) {
l = m +1;
} else {
// arr[m] > t
r = m - 1;
}
}
return ans;
}
}时间复杂度 O(logN)。
思路
假设数组长度为N，首先判断0号位置的数和N-1位置的数是不是峰值位置。
0号位置只需要和1号位置比较，如果0号位置大，0号位置就是峰值位置，可以直接返回。
N-1号位置只需要和N-2号位置比较，如果N-1号位置大，N-1号位置就是峰值位置，可以直接返回。
如果0号位置和N-1在上轮比较中均是最小值，那么数组的样子必然是如下情况：
由上图可知，[0..1]区间内是增长趋势, [N-2...N-1]区间内是下降趋势。
那么峰值位置必在[1...N-2]之间出现。
此时可以通过二分来找峰值位置，先来到中点位置，假设为mid，如果中点位置的值比左右两边的值都大:
arr[mid] > arr[mid+1] && arr[mid] > arr[mid-1]
则mid位置即峰值位置，直接返回。
否则，有如下两种情况：
情况一：mid 位置的值比 mid - 1 位置的值小
趋势如下图：
则在[1...(mid-1)]
Exemple 1 :
Entrée : nums = [1,3,5,6], cible = 5
numL'élément 5 inséré dans ce tableau doit être inséré à la position entre l'élément 3 et l'élément 5, c'est-à-dire la position 2. 🎜🎜Exemple 2 :🎜🎜Entrée : nums = [1,3,5,6], cible = 2🎜🎜Sortie : 1🎜🎜Explication : Si vous souhaitez insérer 2 dans le tableau num L'élément doit être inséré entre l'élément 1 et l'élément 3, c'est-à-dire la position 1. 🎜🎜Exemple 3 :🎜🎜Entrée : nums = [1,3,5,6], cible = 7🎜🎜Sortie : 4🎜🎜Explication : Si vous souhaitez insérer 7 dans le tableau num L'élément doit être inséré à la fin du tableau, c'est-à-dire à la position 4. 🎜🎜Vous pouvez savoir grâce à l'exemple ci-dessus que l'essence de cette question est de trouver la position la plus à gauche qui est supérieure ou égale à un certain nombre dans un tableau ordonné. Si elle n'existe pas, renvoyez la longueur du tableau (en indiquant. qu'il est inséré à la position finale)🎜🎜Nous n'avons qu'à effectuer des modifications simples basées sur l'exemple ci-dessus, lorsque nous trouvons la position qui remplit les conditions, nous retournons<. /code>🎜public class LeetCode_0162_FindPeakElement {
public static int findPeakElement(int[] nums) {
if (nums.length == 1) {
return 0;
}
int l = 0;
int r = nums.length - 1;
if (nums[l] > nums[l + 1]) {
return l;
}
if (nums[r] > nums[r - 1]) {
return r;
}
l = l + 1;
r = r - 1;
while (l <= r) {
int mid = l + ((r - l) >> 1);
if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
return mid;
}
if (nums[mid] < nums[mid + 1]) {
l = mid + 1;
} else if (nums[mid] < nums[mid - 1]) {
r = mid - 1;
}
}
return -1;
}
}Copier après la connexionCopier après la connexion🎜Dans cette question, parce que vous devez trouver la position la plus à gauche, donc lorsquevous rencontrez l'égalité, il vous suffit d'abord d'enregistrer la position, sans revenir directement, puis de continuer vers la gauche pour savoir s'il y a est une position vers la gauche qui remplit les conditions. 🎜🎜En même temps, lorsque vous rencontrez arr[m] > t, vous devez également enregistrer la position m à ce moment-là, car cela peut également être un endroit qui satisfait aux conditions. 🎜🎜Code : 🎜rrreee🎜La complexité temporelle de l'ensemble de l'algorithme est O(logN). 🎜🎜Trouver la première et la dernière position d'un élément dans un tableau trié🎜🎜🎜🎜Réflexion🎜🎜Cette question est également résolue par la dichotomie. Lorsqu'un élément est trouvé par dichotomie, ne vous précipitez pas en arrière, mais continuez à chercher vers la gauche (droite) pour voir si vous pouvez trouver plus La valeur à faire correspondre pour la position gauche (droite). 🎜🎜Le code est le suivant : 🎜rrreee🎜Complexité temporelle O(logN). 🎜🎜Problème de maximum local🎜🎜🎜🎜 Idée 🎜🎜 En supposant que la longueur du tableau est N, déterminez d'abord si le nombre à la position 0 et le nombre à la position N-1</code > Les positions sont des positions de pointe. 🎜🎜La position <code>0 doit uniquement être comparée à la position 1. Si la position 0 est plus grande, le 0</. code> position C'est la position maximale et peut être renvoyée directement. 🎜🎜La position <code>N-1 doit uniquement être comparée à la position N-2 Si la position N-1 est plus grande, <. code>N Position -1 est la position maximale et peut être renvoyée directement. 🎜🎜Si la position 0 et N-1 sont toutes deux des valeurs minimales lors du dernier tour de comparaison, alors le tableau doit ressembler à ce qui suit : 🎜🎜
🎜🎜Comme le montre l'image ci-dessus, [0..1 ]L'intervalle est une tendance croissante, et l'intervalle [N-2...N-1] est une tendance descendante. 🎜🎜Ensuite, la position du pic doit apparaître entre [1...N-2]. 🎜🎜À ce stade, vous pouvez trouver la position maximale par bissection. Allez d'abord à la position médiane, en supposant qu'elle est milieu si la valeur de la position médiane est supérieure. que les valeurs sur les côtés gauche et droit :🎜rrreee🎜La position milieu est la position maximale et est renvoyée directement. 🎜🎜Sinon, on a les deux situations suivantes : 🎜🎜Cas 1 : La valeur de la position médiane est inférieure à la valeur de la position médiane - 1 🎜🎜La tendance est la suivante : 🎜🎜
🎜🎜 continuera dans le [1...(mi- 1)] intervalle Deux points. 🎜🎜Cas 2 : La valeur de la position médiane est inférieure à la valeur de la position médiane + 1🎜🎜La tendance est : 🎜🎜🎜🎜则在[(mid+1)...(N-2)]区间内继续上述二分。
完整代码
public class LeetCode_0162_FindPeakElement {
public static int findPeakElement(int[] nums) {
if (nums.length == 1) {
return 0;
}
int l = 0;
int r = nums.length - 1;
if (nums[l] > nums[l + 1]) {
return l;
}
if (nums[r] > nums[r - 1]) {
return r;
}
l = l + 1;
r = r - 1;
while (l <= r) {
int mid = l + ((r - l) >> 1);
if (nums[mid] > nums[mid + 1] && nums[mid] > nums[mid - 1]) {
return mid;
}
if (nums[mid] < nums[mid + 1]) {
l = mid + 1;
} else if (nums[mid] < nums[mid - 1]) {
r = mid - 1;
}
}
return -1;
}
}时间复杂度O(logN)。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
