 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Application de l'inférence causale dans les incitations micro-vues et les scénarios d'offre et de demande
Application de l'inférence causale dans les incitations micro-vues et les scénarios d'offre et de demande
Application de l'inférence causale dans les incitations micro-vues et les scénarios d'offre et de demande

1. Inférence causale et algorithme d'incitation
1. Contexte commercial et modélisation commerciale
Tout d'abord, présentons brièvement l'expérience commerciale d'incitation à l'enveloppe rouge de Tencent Weishi. À l’instar d’autres produits et scénarios, dans le cadre d’un budget donné, nous accordons des incitations en espèces aux utilisateurs de Tencent Weishi, dans l’espoir de maximiser la rétention des utilisateurs le lendemain et la durée d’utilisation le même jour grâce à des incitations en espèces. La principale forme d'incitation en espèces consiste à distribuer aux utilisateurs, à intervalles irréguliers, des enveloppes rouges en espèces d'un nombre indéfini et d'un montant indéfini. Les trois « incertitudes » mentionnées ci-dessus sont en fin de compte déterminées par des algorithmes. Ces trois « incertitudes » sont également appelées les trois éléments de la stratégie incitative de l’enveloppe rouge.
Parlons ensuite des formes abstraites des différentes stratégies d’incitation en espèces. La première exprime la stratégie sous la forme d'une séquence d'enveloppe rouge, comme par exemple numéroter la séquence d'enveloppe rouge, puis numéroter chaque traitement indépendamment sous forme de one-hot. Son avantage est qu’il peut représenter plus de détails, comme le montant entre chaque enveloppe rouge et d’autres stratégies détaillées, ainsi que les effets correspondants. Cependant, cela nécessitera inévitablement plus de variables pour représenter la stratégie. De plus, davantage de calculs seront nécessaires lors de l'exploration et de la sélection de la stratégie optimale. La deuxième forme, qui utilise un vecteur à trois éléments pour représenter la stratégie, est plus flexible et plus efficace en exploration, mais elle ignore certains détails. La troisième méthode est plus mathématique, c'est-à-dire que la séquence d'enveloppe rouge devient directement une fonction autour du temps t, et les paramètres de la fonction peuvent former un vecteur pour représenter la stratégie. La modélisation des problèmes causals et la représentation des stratégies déterminent grandement l’exactitude et l’efficacité de l’estimation des effets causals.
En supposant que nous disposons d'une bonne abstraction politique et d'une bonne représentation vectorielle, la prochaine chose à faire est de choisir un cadre algorithmique. Il y a trois cadres ici. Le premierframework est relativement mature dans l'industrie, qui utilise l'inférence causale combinée à l'optimisation de contraintes multi-objectifs pour allouer et optimiser les stratégies. Dans ce cadre, l'inférence causale est principalement responsable de l'estimation des principaux indicateurs d'utilisateurs correspondant à différentes stratégies, ce que nous appelons la rétention des utilisateurs et l'amélioration de la durée. Après estimation, nous utilisons une optimisation contrainte multi-objectifs pour effectuer une allocation de stratégie budgétaire hors ligne afin de satisfaire les contraintes budgétaires. Le deuxième type est l'apprentissage par renforcement hors ligne combiné à une méthode d'optimisation de contraintes multi-objectifs. Personnellement, je pense que cette méthode est plus prometteuse pour deux raisons principales. La première raison est que dans les scénarios d'application réels, il existe de nombreuses stratégies, et l'apprentissage par renforcement lui-même peut explorer efficacement l'espace stratégique. En même temps, parce que nos stratégies sont dépendantes, l'apprentissage par renforcement peut modéliser la dépendance entre les stratégies. que l’essence de la chimie forte hors ligne est en réalité un problème d’estimation contrefactuelle, qui possède elle-même de fortes propriétés causales. Malheureusement, dans notre scénario, nous avons essayé la méthode d’apprentissage par renforcement hors ligne, mais son effet en ligne n’a pas produit l’effet souhaité. La raison en est, d’une part, notre problème de méthode, et d’autre part, il est principalement limité par les données. Afin de former un bon modèle d'apprentissage par renforcement hors ligne, la distribution des stratégies dans les données doit être suffisamment large, ou la distribution des stratégies est suffisamment uniforme. En d'autres termes, que nous utilisions des données aléatoires ou des données d'observation, nous espérons explorer autant de stratégies de ce type que possible, et la distribution sera relativement uniforme, afin que nous puissions réduire le nombre de contrefactuels. Le dernier cadre d'algorithme est relativement mature dans les scénarios publicitaires. Nous utilisons l'apprentissage par renforcement en ligne pour contrôler le trafic et le budget. L’avantage de cette méthode est qu’elle peut répondre aux urgences en ligne de manière opportune et rapide, et en même temps, elle peut contrôler le budget avec plus de précision. Après l'introduction de la cause et de l'effet, l'indicateur que nous utilisons pour la sélection ou le contrôle du trafic n'est plus l'indicateur ECPM. Il peut s'agir d'une amélioration de la rétention et de la durée que nous estimons maintenant. Après une série de tentatives pratiques, nous avons finalement choisi le premier cadre algorithmique, qui est une inférence causale combinée à une optimisation de contraintes multi-objectifs, car il est plus stable et contrôlable, et il repose également moins sur l'ingénierie en ligne.
Le pipeline du premier cadre d'algorithme est présenté dans la figure ci-dessous. Tout d'abord, les caractéristiques des utilisateurs sont calculées hors ligne, puis un modèle causal est utilisé pour estimer l'amélioration des indicateurs de base des utilisateurs dans le cadre de différentes stratégies, ce qu'on appelle l'amélioration. Sur la base de l'amélioration estimée, nous utilisons l'optimisation multi-objectifs pour résoudre et attribuer la stratégie optimale. Afin d'accélérer le calcul de l'ensemble du processus, nous regrouperons la foule à l'avance lors de la structuration, ce qui signifie que nous pensons que les personnes de ce cluster ont la même cause et le même effet, et par conséquent, nous attribuons la même stratégie aux personnes dans le même cluster.

2. Hypothèse stratégique et diagramme de causalité
Sur la base de la discussion ci-dessus, concentrons-nous sur la façon d'abstraire la stratégie. Voyons d’abord comment nous résumons le diagramme de causalité. La cause et l'effet qui doivent être modélisés dans le scénario d'incitation à l'enveloppe rouge se reflètent dans plusieurs jours et plusieurs enveloppes rouges. Étant donné que l'enveloppe rouge précédente affectera certainement la réception ou non de l'enveloppe rouge suivante, il s'agit essentiellement d'un problème d'effet de traitement variable dans le temps, résumé dans un diagramme de causalité en série chronologique, comme indiqué à droite.
En prenant comme exemple plusieurs enveloppes rouges en une journée, tous les indices de T représentent un numéro de série de l'enveloppe rouge. T représente à cet instant le vecteur constitué du montant de l'enveloppe rouge actuelle et de l'intervalle de temps depuis l'émission de la dernière enveloppe rouge. Y est la durée d'utilisation actuelle de l'utilisateur après l'émission de l'enveloppe rouge et l'augmentation de la rétention le lendemain. X est la variable de confusion observée jusqu'au moment présent, comme le comportement de visionnage de l'utilisateur ou les attributs démographiques, etc. Bien entendu, il existe de nombreuses variables confusionnelles inobservées, représentées par U, comme les séjours occasionnels ou les arrêts occasionnels des utilisateurs. Une variable confondante non observée importante est l'esprit de l'utilisateur, qui comprend principalement l'évaluation par l'utilisateur du montant des incitations de l'enveloppe rouge. Ces soi-disant esprits sont difficiles à représenter à travers certaines statistiques ou caractéristiques statistiques au sein du système.
Il serait très compliqué de modéliser la stratégie de l'enveloppe rouge sous forme de séries chronologiques, nous avons donc procédé à quelques simplifications raisonnables. Par exemple, supposons que U n'affecte que T, X et Y au moment présent, et qu'il n'affecte U qu'au moment suivant, c'est-à-dire l'esprit de l'utilisateur. C'est-à-dire que cela n'affectera le futur Y qu'en affectant l'évaluation des valeurs ou la mentalité du moment suivant. Mais même après une série de simplifications, nous constaterons que l’ensemble du diagramme causal des séries chronologiques reste très dense, ce qui rend difficile la réalisation d’estimations raisonnables. Et lorsque l’on utilise les méthodes G pour résoudre l’effet de tendance variable dans le temps, une grande quantité de données est nécessaire pour la formation. Cependant, en réalité, les données que nous obtenons sont très rares, il est donc difficile d’obtenir un bon effet en ligne. Au final, nous avons fait beaucoup de simplifications et avons obtenu la structure du fork (Fork) comme sur l'image en bas à droite. Nous avons réalisé une agrégation de toutes les stratégies d'enveloppe rouge pour la journée, qui est un vecteur composé de trois éléments de la stratégie (montant total des incitations à enveloppe rouge, durée totale et nombre total), représentés par T. X est une variable confusionnelle au temps T-1, qui correspond au comportement historique et aux attributs démographiques de l'utilisateur à ce jour. Y représente la durée d'utilisation de l'utilisateur ce jour-là, qui est l'indicateur de durée de rétention ou d'utilisation de l'utilisateur pour le jour suivant. Bien que cette méthode semble ignorer de nombreux détails, comme l’interaction entre les enveloppes rouges. Mais d’un point de vue macro, cette stratégie est plus stable et ses effets peuvent être mieux mesurés.

3. Représentation de la stratégie et modèle causal
Sur la base de la discussion ci-dessus, la prochaine étape est la question centrale, c'est-à-dire comment représenter la stratégie (le traitement). Auparavant, nous avons essayé d'utiliser One-Hot pour numéroter indépendamment les vecteurs à trois éléments, séparer les trois éléments et utiliser la fonction temps pour construire un traitement multivariable. Les deux premières stratégies sont plus faciles à comprendre. Ensuite, la dernière méthode sera présentée. Regardez l'image ci-dessus. Nous avons construit les fonctions sinusoïdales des trois éléments par rapport à t respectivement, c'est-à-dire qu'étant donné un temps T, nous pouvons obtenir respectivement la quantité, l'intervalle de temps et le nombre. Nous utilisons les paramètres correspondant à ces fonctions comme éléments du nouveau vecteur, similaire à la représentation des trois éléments de la stratégie. Le but de l'utilisation d'une fonction pour représenter la stratégie est de conserver plus de détails, car les deux premières méthodes ne peuvent connaître la quantité moyenne d'enveloppes rouges et d'intervalles de distribution que par une combinaison de stratégies, et l'utilisation d'une fonction peut la représenter plus en détail. Cependant, cette méthode peut introduire davantage de variables et rendre le calcul plus complexe.
Une fois la stratégie représentée, le modèle causal peut être sélectionné pour estimer l'effet causal. Sous la forme de One-Hot représentant les trois éléments de T, nous utilisons le modèle x-Learner pour modéliser chaque stratégie et utilisons la stratégie avec le plus petit montant total comme stratégie de base pour calculer et évaluer l'effet de traitement de toutes les stratégies. Dans ce cas, vous pourriez avoir l’impression que son efficacité est très faible et que le modèle manque de généralisation. Par conséquent, nous adoptons en outre la troisième stratégie que nous venons de mentionner, à savoir utiliser un vecteur d’éléments de fonction sinusoïdale pour former un traitement. Un seul modèle DML est ensuite utilisé pour estimer les performances de toutes les stratégies par rapport à la stratégie de référence. De plus, nous avons également réalisé une optimisation DML, en supposant que y est une pondération linéaire de la variable de confusion et de l'effet causal, c'est-à-dire que y est égal à l'effet du traitement plus la variable de confusion. De cette manière, les termes d’intersection et les termes d’ordre supérieur entre les éléments vectoriels sont construits artificiellement. Cela équivaut à construire une fonction de noyau polynomial pour introduire des fonctions non linéaires. Sur cette base, le DML s’est grandement amélioré par rapport à la stratégie de base. De l'analyse de la figure ci-dessous, nous pouvons constater que le modèle DML coûte moins cher et améliore le retour sur investissement, ce qui signifie que nous pouvons utiliser les ressources plus efficacement.
Plus tôt, nous avons principalement discuté de certaines abstractions de méthodes et de choix de modèles. Dans le processus de pratique, nous trouverons également des problèmes commerciaux biaisés, tels que. comme traitement lorsque vous faites du One-Hot ? À cette époque, nous avons mis en œuvre une stratégie d’expansion lot par lot. Commencez par élaborer une stratégie de semences à travers les trois éléments de la stratégie, puis sélectionnez et conservez manuellement les semences de haute qualité, puis développez-la. Après l'expansion, nous lancerons de nouvelles stratégies par lots en fonction d'une période de temps, comme les deux premières semaines de lancement, et veillerons à ce que la taille du trafic aléatoire de chaque stratégie soit cohérente ou comparable. Dans ce processus, l’impact des facteurs temporels sera en effet ignoré et les stratégies moins efficaces seront continuellement remplacées, enrichissant ainsi l’ensemble des stratégies. De plus, le facteur temps affectera certainement la comparabilité des stratégies de trafic aléatoire. Par conséquent, nous avons construit une méthode similaire à la rotation des tranches de temps pour garantir que les tranches de temps couvertes sont cohérentes, éliminant ainsi l'impact des facteurs temporels sur la stratégie, afin que le trafic aléatoire obtenu puisse être utilisé pour entraîner le modèle.
Et comment générer de nouvelles stratégies ? Une méthode simple consiste à utiliser la recherche par grade ou un algorithme génétique. Ce sont des algorithmes généraux de recherche plus courants. De plus, nous pouvons combiner l’élagage manuel, comme la suppression de certains types de séquences d’enveloppes rouges indésirables. Une autre méthode consiste à utiliser BanditNet, qui est une méthode d'apprentissage par renforcement hors ligne pour calculer des stratégies invisibles, c'est-à-dire estimer l'effet contrefactuel, puis utiliser la valeur estimée pour sélectionner la stratégie. Bien entendu, nous devrons éventuellement utiliser le trafic aléatoire en ligne pour le vérifier. La raison en est que la variance de cette méthode d’apprentissage par renforcement hors ligne sera probablement très grande.

4. Enjeux stratégiques et itération
En plus des problèmes évoqués ci-dessus, nous rencontrerons également des problèmes d'ordre business. La première question est : quel est le cycle de mise à jour des politiques utilisateur ? Serait-il préférable que toutes les politiques utilisateur soient mises à jour fréquemment ? À cet égard, notre expérience pratique varie d’une personne à l’autre. Par exemple, les stratégies destinées aux utilisateurs fréquents devraient évoluer plus lentement. D'une part, cela est dû au fait que les utilisateurs fréquents connaissent déjà notre format, y compris le montant de l'incitation. Si le montant de l'enveloppe rouge change radicalement, cela affectera certainement les indicateurs correspondants. Par conséquent, nous maintenons en fait une stratégie de mise à jour hebdomadaire pour les utilisateurs à haute fréquence, mettant à jour une fois par semaine, mais pour les nouveaux utilisateurs, le cycle de mise à jour est plus court ; La raison en est que nous en savons très peu sur les nouveaux utilisateurs et que nous souhaitons pouvoir explorer plus rapidement les stratégies appropriées et réagir rapidement pour apporter des changements de stratégie en fonction des interactions des utilisateurs. Étant donné que le comportement des nouveaux utilisateurs est également très clairsemé, dans ce cas, nous utiliserons le niveau quotidien pour mettre à jour les nouveaux utilisateurs ou certains utilisateurs peu fréquents. De plus, nous devons également surveiller la stabilité de la stratégie pour éviter l'impact du bruit des fonctionnalités. Le pipeline que nous avons construit est illustré à droite. Ici, nous surveillerons si l'effet du traitement est stable, et nous surveillerons également quotidiennement la stratégie finale assignée par l'utilisateur, comme la différence entre la stratégie d'aujourd'hui et la stratégie d'hier, y compris le montant et le nombre. Nous prendrons également régulièrement des instantanés de la stratégie en ligne, principalement pour le débogage et la lecture rapide afin de garantir la stabilité de la stratégie. De plus, nous mènerons également des expériences sur le petit trafic et surveillerons sa stabilité. Seules les expériences sur le petit trafic répondant aux exigences de stabilité seront utilisées pour remplacer les stratégies existantes.
La deuxième question est de savoir si les stratégies pour les nouveaux utilisateurs et certains utilisateurs spéciaux sont indépendantes ? La réponse est oui. Par exemple, pour les nouveaux utilisateurs, nous leur fournirons d’abord une forte incitation, puis l’intensité de l’incitation diminuera avec le temps. Une fois que l'utilisateur entre dans le cycle de vie normal, nous mettrons en œuvre des stratégies d'incitation régulières pour lui. Parallèlement, pour les groupes sensibles particuliers, il y aura une politique de restriction sur leur montant. Pour cela, nous formerons également des modèles indépendants pour s'adapter à ce groupe de personnes.
La troisième question que vous pouvez vous poser est la suivante : quelle est l'importance de l'inférence causale dans l'ensemble du cadre algorithmique ? D’un point de vue théorique, nous pensons que l’inférence causale est essentielle car elle apporte de grands avantages aux algorithmes d’incitation. Par rapport aux modèles de régression et de classification, l'inférence causale est cohérente avec les objectifs commerciaux et est intrinsèquement orientée vers le retour sur investissement, elle apportera donc des objectifs d'optimisation concernant le degré d'amélioration. Cependant, nous souhaitons rappeler à tous que lorsque nous allouons des budgets, nous ne pouvons pas choisir la stratégie optimale pour chaque utilisateur et que l’effet causal est relativement faible par rapport aux individus. Lorsque nous allouons des budgets, il est très probable que certaines différences dans les effets causals des utilisateurs seront éliminées. À l’heure actuelle, notre optimisation contrainte affectera grandement l’effet stratégique. Par conséquent, lors du clustering, nous avons également essayé davantage de méthodes de clustering, telles que la méthode de clustering profond SCCL, pour obtenir de meilleurs résultats de clustering. Nous avons également réalisé quelques itérations de modèles causals profonds, comme BNN ou Dragonnet, etc.
Nous avons constaté qu'au cours de la pratique, les indicateurs hors ligne du modèle causal profond se sont effectivement améliorés de manière significative, mais son effet en ligne n'est pas suffisamment stable. La raison principale est l'apparition de valeurs manquantes. Dans le même temps, nous avons également constaté que la méthode de planification des fonctionnalités affecte grandement la stabilité du modèle d'apprentissage profond en ligne, donc en fin de compte, nous aurons tendance à utiliser la méthode DML de manière stable.
C'est tout pour partager sur les scénarios d'incitation. Ensuite, j'aimerais demander à deux autres étudiants de notre équipe de partager avec vous quelques explorations pratiques et théoriques sur les scénarios d'optimisation de l'offre et de la demande.

2. Inférence causale et ajustement de l'offre et de la demande
1. Contexte commercial et modélisation commerciale
Ensuite, introduisons le contexte commercial de Tencent Microvision en termes d'offre et de demande. En tant que plate-forme vidéo courte, Weishi propose de nombreuses catégories de vidéos différentes. Pour les groupes d'utilisateurs ayant des intérêts de visionnage parfois différents, nous devons répartir de manière appropriée la proportion d'exposition ou la proportion d'inventaire de chaque catégorie en fonction des différentes caractéristiques de l'utilisateur. L'objectif est d'améliorer l'expérience utilisateur et le temps de visionnage de l'utilisateur, parmi lesquels l'expérience de l'utilisateur peut être. mesuré sur la base de l'indicateur de taux de balayage rapide de 3 secondes, et le temps de visionnage est principalement mesuré sur la base de la durée totale de lecture. Comment ajuster le taux d'exposition ou le taux d'inventaire des catégories de vidéos ? La principale méthode que nous envisageons est d'augmenter ou de diminuer certaines catégories proportionnellement. Le rapport d'augmentation et de diminution est une valeur prédéfinie.
Ensuite, nous devons utiliser des algorithmes pour déterminer comment décider quelles catégories augmenter et quelles catégories diminuer, afin de maximiser l'expérience utilisateur et le temps de visionnage, et en même temps, nous devons répondre à certaines contraintes telles que comme limites d’exposition totale. Cet endroit résume trois idées principales de modélisation. La première est une idée plus simple, c'est-à-dire que nous traitons directement l'augmentation et la diminution comme une variable de traitement de 0 et 1, nous estimons son effet causal, puis effectuons une optimisation contrainte multi-objectif pour obtenir une stratégie finale. La deuxième idéeest de modéliser le traitement plus précisément. Nous traitons le traitement comme une variable continue. Par exemple, le taux d’exposition d’une catégorie est une variable qui évolue continuellement entre 0 et 1. Ajustez ensuite une courbe d'effet causal ou une fonction d'effet causal correspondante, puis effectuez une optimisation contrainte multi-objectif et obtenez enfin la stratégie finale. On peut noter que les deux méthodes qui viennent d’être évoquées sont des méthodes en deux étapes. La troisième idée, Nous introduisons des contraintes dans l'estimation des effets causals pour obtenir une stratégie optimale qui satisfait les contraintes. C’est aussi le contenu de la recherche que j’espère partager avec vous plus tard.
Tout d’abord, concentrons-nous sur les deux premières idées de modélisation. Il y a plusieurs points de modélisation auxquels il faut prêter attention. Le premier point est que pour garantir l’exactitude de l’estimation de l’effet causal, nous devons diviser la population et estimer l’effet causal du traitement binaire ou du traitement continu sur chaque population. Tout à l'heure, le professeur Zheng a également mentionné des méthodes de classification des personnes, telles que l'utilisation du regroupement Kmeans ou d'un regroupement profond. Le deuxième point est de savoir comment évaluer l'effet du modèle sur des données expérimentales non aléatoires. Par exemple, nous devons évaluer l'effet du modèle hors ligne sans faire de test AB. Concernant cette question, vous pouvez vous référer à certains indicateurs mentionnés dans le document indexé ci-dessus dans le PPT pour une évaluation hors ligne. Le troisième point à noter est qu’il faut considérer autant que possible la corrélation et l’influence mutuelle entre catégories, comme certains problèmes d’éviction entre catégories similaires, etc. Si ces facteurs peuvent être inclus dans l’estimation des effets causals, de meilleurs résultats devraient être obtenus.

2. Stratégie d'ajustement de la proportion d'exposition à un seul groupe × catégorie
Ensuite, nous développerons ces idées de modélisation en détail. Tout d'abord, la première méthode de modélisation consiste à définir un traitement de 0 et 1, qui sert à représenter les moyens d'augmenter ou de diminuer ces deux types d'intervention. Vous pouvez vous référer au bref diagramme de cause à effet à gauche. , où x représente certaines caractéristiques de l'utilisateur, telles que le comportement de fonctionnement historique, les caractéristiques statistiques pertinentes, ainsi que d'autres attributs de l'utilisateur, etc. y est l'objectif qui nous intéresse, qui est le taux d'accélération de 3 secondes ou la durée totale de lecture. En outre, il est également nécessaire de prêter attention à certaines variables confusionnelles inobservées, telles que le balayage et la sortie accidentels et rapides des utilisateurs, et le même utilisateur peut en fait être utilisé par plusieurs personnes, ce qui est également un problème d'identités multiples des utilisateurs. De plus, l'itération et la mise à jour continues de la stratégie de recommandation auront également un impact sur les données d'observation, et la migration des intérêts des utilisateurs est également en dehors de l'observation. Ces variables confusionnelles non observées peuvent affecter dans une certaine mesure l’estimation des effets causals.
Pour ce type de modélisation, des méthodes courantes d'estimation des effets causals peuvent être résolues. Par exemple, vous pouvez considérer T-Learner ou X-Learner, ou DML, qui peuvent estimer les effets causals. Bien entendu, cette méthode de modélisation simple présente également certains problèmes. Par exemple, si nous utilisons un traitement binaire pour modéliser, elle sera trop simplifiée. De plus, selon cette méthode, chaque catégorie est considérée séparément et la corrélation entre les catégories n’est pas prise en compte. Le dernier problème est que nous n'avons pas pris en compte des facteurs spécifiques tels que l'ordre d'exposition et la qualité du contenu dans l'ensemble de la question.
Ensuite, introduisons la deuxième idée de modélisation. Nous considérons toutes les catégories ensemble. Par exemple, nous avons k catégories de vidéos et supposons que le traitement soit un vecteur de cause à k dimensions. Chaque position du vecteur représente une catégorie, comme les émissions de variétés cinématographiques et télévisées ou les événements MOBA, etc. 0 et 1 représentent toujours des augmentations ou des diminutions. À l’heure actuelle, l’estimation de l’effet causal du traitement dans des vecteurs multidimensionnels peut être résolue par l’algorithme DML. Nous traitons généralement le vecteur de traitement, qui est entièrement nul, comme contrôle. Bien que cette méthode résolve le problème du fait que chaque catégorie n’est pas considérée séparément, elle présente néanmoins certains problèmes potentiels. Le premier est le problème de l'explosion de dimensionnalité provoquée par un trop grand nombre de catégories. À mesure que les dimensions augmentent, puisqu'il existe deux situations de 0 et 1 à chaque position, le nombre de permutations et de combinaisons potentielles augmentera de façon exponentielle, ce qui affectera la cause et l'effet. . La précision des estimations des effets crée des interférences. De plus, les facteurs mentionnés précédemment tels que la séquence d’exposition et le contenu ne sont pas pris en compte.

Après avoir partagé les idées de modélisation du traitement des variables binaires, nous pouvons ensuite modéliser le traitement de manière plus détaillée et plus conforme à ses propres caractéristiques. Nous avons remarqué que le taux d'exposition lui-même est une variable continue, il est donc plus raisonnable pour nous d'utiliser un traitement continu pour la modélisation. Selon cette idée de modélisation, nous devons d’abord diviser la foule. Pour chaque groupe de personnes, nous modélisons chaque catégorie séparément pour obtenir une courbe d'effet causal d'un seul groupe * une seule catégorie. Comme le montre l'image de gauche, la courbe des effets causals représente l'impact de la proportion de différentes catégories sur les objectifs qui nous tiennent à cœur. Afin d'estimer une telle courbe d'effet causal, je partage principalement deux algorithmes réalisables, l'un est DR-Net et l'autre est VC-Net. Les deux algorithmes appartiennent à la catégorie de l'apprentissage profond. La structure du modèle est celle indiquée sur l'image de droite.
Tout d’abord, présentons DR-Net. L'entrée x du modèle passera d'abord par plusieurs couches entièrement connectées pour obtenir une représentation implicite appelée z. DR-Net adopte une stratégie de discrétisation, qui divise le traitement continu en plusieurs blocs, puis chaque bloc entraîne un sous-réseau pour prédire la variable cible. Puisque DR-Net adopte une stratégie de discrétisation, la courbe d'effet causal finale qu'il obtient n'est pas strictement continue, mais à mesure que la discrétisation devient plus fine, l'estimation finale se rapprochera d'une courbe continue. Bien entendu, à mesure que la segmentation idéalisée devient plus fine, elle apportera plus de paramètres et un risque plus élevé de surajustement. Ensuite, je parlerai de VC-Net. VC-Net améliore dans une certaine mesure les défauts de DR-Net. Tout d'abord, l'entrée du modèle VC-Net est toujours X, qui est également la caractéristique de l'utilisateur. Il obtient également d’abord une représentation implicite Z après plusieurs couches entièrement connectées. Mais en Z, un module de prédiction du Propensity Score sera connecté en premier. Dans des conditions de traitement continu, la propension est une densité de probabilité de traitement t dans une condition X donnée, qui est également π représentée sur la figure. Examinons ensuite la structure du réseau après Z. Contrairement à l'opération de discrétisation de DR-Net, VC-Net utilise une structure de réseau à coefficient variable, c'est-à-dire que chaque paramètre du modèle après Z est un paramètre concernant la fonction t. Les auteurs de la littérature que nous avons mentionnés ici ont utilisé la méthode des fonctions de base pour exprimer chaque fonction comme une combinaison linéaire de fonctions de base, également écrite sous la forme θ(t). De cette manière, l’estimation de la fonction devient l’estimation paramétrique de la combinaison linéaire des fonctions de base. Ainsi, de cette façon, l'optimisation des paramètres du modèle n'est pas un problème, et la courbe des effets causals obtenue par VC-Net est également une courbe continue. La fonction objectif à résoudre par VC-Net se compose de plusieurs parties. D’une part, il s’agit du carré de la perte de la prédiction finale sur la cible, qui est μ sur la figure. D’autre part, il s’agit également de la perte logarithmique de la densité de probabilité de propension. En plus de ces deux parties, l'auteur ajoute également un terme de pénalité appelé régularisation ciblée à la fonction objectif, afin que des propriétés d'estimation doublement robustes puissent être obtenues. Pour des détails spécifiques, les amis intéressés peuvent se référer aux deux articles originaux répertoriés ci-dessus pour plus de détails. 
Enfin, ouvrons la voie à un morceau de nos recherches que nous partagerons avec vous prochainement. Nous avons remarqué que la proportion d'exposition de chaque catégorie vidéo est un vecteur continu multidimensionnel. La raison pour laquelle il est multidimensionnel est que nous avons plusieurs catégories de vidéos et que chaque dimension représente une catégorie de vidéo. La principale raison pour laquelle il est continu est que la proportion d'exposition de chaque catégorie vidéo est continue et que ses valeurs sont comprises entre 0 et 1. En même temps, il existe une contrainte naturelle, qui est que le taux d'exposition total de toutes nos catégories de vidéos doit être égal à 1. Nous pouvons donc considérer un tel vecteur continu multidimensionnel comme traitement.
Le vecteur illustré à droite en est un exemple. Notre objectif est de trouver le rapport d’exposition optimal pour maximiser notre temps de jeu total. Dans le cadre causal traditionnel, il est difficile pour les algorithmes de résoudre un problème aussi multidimensionnel, continu et sans contrainte. Ensuite, nous partageons nos recherches sur cette question.

3. Partage du modèle causal multivariable continu contraint
MDPP Forest Ce travail est une méthode d'exploration et une solution innovante au problème réalisée par l'équipe lors de l'étude des problèmes d'offre et de demande. Notre équipe a découvert à cette époque que face au problème de l'attribution du meilleur rapport d'exposition aux catégories vidéo pour chaque utilisateur, les autres méthodes courantes existantes ne pouvaient pas aboutir à un résultat plus conforme aux attentes. Par conséquent, après une période d'essai et d'amélioration, la méthode conçue par notre équipe peut obtenir de bons résultats hors ligne, puis coopérer avec des recommandations et enfin obtenir certains avantages stratégiques. Nous avons ensuite compilé ce travail dans un article qui a eu la chance d’être publié sur KDD 2022.

1. Contexte et défis
Tout d'abord, présentez le contexte du problème. En termes d'offre et de demande, nous divisons les courtes vidéos en différentes catégories en fonction du contenu, comme la vulgarisation scientifique, le cinéma et la télévision, la nourriture en plein air, etc. Le taux d’exposition des catégories de vidéos fait référence à la proportion de chacune de ces différentes catégories de vidéos parmi l’ensemble des vidéos regardées par un utilisateur. Les utilisateurs ont des préférences très différentes pour différentes catégories, et les plateformes doivent souvent déterminer le taux d’exposition optimal pour chaque catégorie au cas par cas. Lors de la phase de réorganisation, la recommandation de différents types de vidéos est contrôlée. Un grand défi pour l'entreprise est de savoir comment allouer le meilleur ratio d'expositions vidéo pour maximiser le temps de chaque utilisateur sur la plateforme.

La principale difficulté d'un tel problème réside dans les trois points suivants. La première est que dans le système de recommandation de vidéos courtes, les vidéos que chaque utilisateur verra auront une très forte corrélation avec ses propres caractéristiques. Il s'agit d'un biais sélectif. Par conséquent, nous devons utiliser des algorithmes liés à l’inférence causale pour éliminer les biais. La seconde est que le taux d’exposition de la catégorie vidéo est un traitement continu, multidimensionnel et contraint. Il n’existe actuellement aucune méthode très aboutie pour résoudre des problèmes aussi complexes dans les domaines de l’inférence causale et de l’optimisation des politiques. La troisième est que dans les données hors ligne, nous ne connaissons pas a priori le véritable taux d’exposition optimal de chaque personne, il est donc difficile d’évaluer cette méthode. Dans un environnement réel, ce n'est qu'un sous-lien dans la recommandation. Les résultats expérimentaux finaux ne peuvent pas juger de l'exactitude de cette méthode pour ses propres objectifs de calcul. Il nous est donc difficile d’évaluer avec précision le problème de ce scénario. Nous présenterons plus tard comment nous effectuons l’évaluation des effets.

2. Définition du problème
Nous résumons d'abord les données dans un diagramme de causalité en statistiques. Parmi eux, le vecteur. Y est le temps de visionnage de l'utilisateur, qui est la réponse à l'objectif de la tâche. L'objectif de notre modélisation est de donner un rapport d'exposition de catégorie vidéo optimal en haute dimension sous des caractéristiques spécifiques de l'utilisateur X, de manière à maximiser le temps de visionnage attendu par l'utilisateur. Ce problème semble être simplement représenté par un diagramme ternaire causal, mais il existe un gros problème, mentionné précédemment, notre traitement est le taux d'exposition de plusieurs catégories, qui est pris en compte par le rapport d'exposition des catégories qui construit un vecteur multidimensionnel. avec des valeurs continues et la somme des vecteurs est 1. Ce problème est plus compliqué.

3. Introduction à la méthode - Forêt de point de préférence de différence maximale (MDP2)
À cet égard, notre méthode est également basée sur la forêt de décision causale (forêt causale). Les arbres de décision causale générale ne peuvent résoudre des problèmes de traitement qu’avec des valeurs discrètes unidimensionnelles. En améliorant le calcul de la fonction de critère de division intermédiaire, nous ajoutons des informations continues de haute dimension pendant la division, afin qu'elle puisse résoudre le problème des valeurs continues de haute dimension et du traitement contraint.

① Introduction à la méthode - problème continu
Tout d'abord, nous résolvons le problème du traitement continu. Comme le montre la figure, l’effet de T sur Y est une courbe continue. Supposons d’abord qu’il s’agisse d’une courbe croissante de façon monotone. Pour toutes les valeurs de traitement dans les données, nous les parcourons et calculons la moyenne Y des échantillons gauche et droit pour trouver le point avec la plus grande différence entre la moyenne Y à gauche et la moyenne Y à droite, c'est-à-dire le point présentant le bénéfice causal moyen le plus important. Nous appelons ce point le point de différence maximum, qui est le point le plus efficace sur l'espace de traitement continu, ce qui signifie que le traitement peut modifier considérablement Y. Le point de différence maximum est le point que nous voulons obtenir dans une seule dimension.
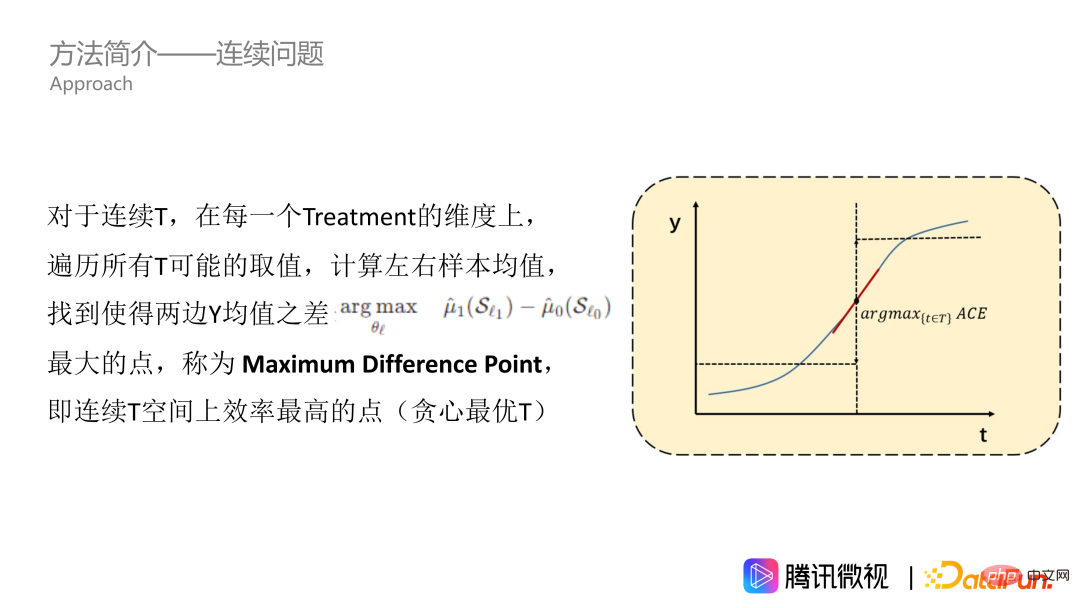
Cependant, la méthode que nous venons d'évoquer ne convient qu'aux courbes croissantes de façon monotone. Mais en fait, la plupart des problèmes ne sont pas si graves, notamment celui du taux d'exposition. Sur cette question, la courbe d’effet a généralement la forme d’une montagne, c’est-à-dire qu’elle augmente d’abord puis diminue. Recommander davantage de vidéos que les utilisateurs aiment peut augmenter la durée de visionnage des utilisateurs. Cependant, si ce type est trop recommandé, l'ensemble de la recommandation vidéo deviendra très ennuyeux et évincera également l'espace d'exposition des types de vidéos appréciés des autres utilisateurs. La courbe a donc généralement la forme d’une montagne, mais elle peut également avoir d’autres formes. Afin de nous adapter à la courbe en T de n'importe quelle forme, nous devons effectuer une opération intégrale, c'est-à-dire trouver l'intervalle de plage de valeurs pour l'accumulation. Sur la courbe accumulée, on calcule également les valeurs moyennes des côtés gauche et droit, ainsi que le point où la différence entre les valeurs moyennes des deux côtés est la plus grande, comme l'étoile à cinq branches dans la photo. Ce point peut être appelé le point de préférence de différence maximale, qui est notre MDPP.

② Introduction à la méthode - problème de grande dimension #🎜 🎜#
Ci-dessus nous avons présenté comment résoudre le problème continu, mais la courbe qui vient d'être mentionnée n'est qu'unidimensionnelle et correspond à une seule catégorie vidéo. Ensuite, nous utilisons l'idée de traversée heuristique de dimension pour résoudre des problèmes multidimensionnels. Lors du calcul du score de classification, nous utilisons une idée heuristique pour trier aléatoirement les K dimensions et calculer une agrégation d'indicateurs D dans chaque dimension, c'est-à-dire effectuer une opération de sommation. Obtenez D* comme entropie d'informations de grande dimension, puis considérez la contrainte. La contrainte est que la somme de tous les MDPP est 1. Ici, nous devons considérer les deux situations suivantes. La première est si la somme de MDPP n'atteint pas 1 après le franchissement de la dimension K. En réponse à cette situation, nous ajouterons la somme de tous les MDPP et les normaliserons à 1. Le deuxième cas est que si l'on parcourt uniquement la dimension K', qui est plus petite que la dimension K, la somme des MDPP atteint 1. Pour cela, nous arrêterons le parcours et fixerons le MDPP au "montant de ressource" restant, soit 1 moins la somme des valeurs MDPP précédemment calculées, afin que les contraintes puissent être prises en compte.

De plus, nous allons également La forêt est introduite dans la structure arborescente ci-dessus car elle a deux significations principales. La première est notre idée traditionnelle d’ensemble d’ensachage, qui peut utiliser plusieurs apprenants pour améliorer la robustesse du modèle. La seconde est que dans le parcours dimensionnel, seules les dimensions K' seront calculées à chaque fois qu'un nœud est divisé, et certaines dimensions ne sont pas incluses. Pour que chaque dimension ait une chance égale de participer à la scission, nous devons construire plusieurs arbres.

③ Introduction à la méthode - accélération de l'algorithme#🎜🎜 #
Il y a aussi un autre problème. Étant donné que l'algorithme contient trois niveaux de parcours, tous les modèles d'arbre nécessitent un parcours de valeurs de caractéristiques, ainsi qu'un parcours de dimension supplémentaire et un parcours de recherche de MDPP. . Une telle traversée à trois couches rend l’efficacité très faible. Par conséquent, nous utilisons la méthode du graphe quantile pondéré pour le parcours des valeurs propres et le parcours MDPP, et calculons uniquement les résultats correspondants aux points quantiles, ce qui peut réduire considérablement la complexité de l'algorithme. Dans le même temps, nous avons également trouvé ces points quantiles comme points limites de la « plage de valeurs cumulées », ce qui peut réduire considérablement la quantité de calcul et de stockage. En supposant qu’il existe q quantiles, il suffit de calculer q fois pour obtenir le nombre d’échantillons et la valeur moyenne de y dans chaque intervalle quantile. De cette façon, chaque fois que nous calculons la différence d entre les moyennes des deux côtés, nous calculons uniquement. besoin de diviser la valeur q par la gauche. Pour les deux parties de droite, faites simplement une somme pondérée des valeurs moyennes dans chaque intervalle. Nous n'avons plus besoin de recalculer la moyenne de tous les échantillons à gauche et à droite du point quantile. Entrons dans la partie expérimentale ci-dessous.

4. Conception expérimentale
① Conception expérimentale-métrique
Notre évaluation expérimentale est essentiellement un problème d'évaluation de stratégie, nous avons donc introduit des indicateurs liés à l'évaluation de stratégie. Le premier est le Main Regret, qui mesure l’écart entre le rendement global de la stratégie et le rendement optimal théorique. L'autre est l'erreur carrée du traitement principal, qui est utilisée pour mesurer l'écart entre la valeur estimée et la valeur optimale de chaque dimension de traitement dans le cadre d'un traitement multidimensionnel. Pour les deux indicateurs, plus c’est petit, mieux c’est. Cependant, le plus gros problème posé par la définition de ces deux indicateurs d’évaluation est de savoir comment déterminer la valeur optimale.

② Méthode de comparaison de plans expérimentaux
Présentez notre méthode de comparaison. La première concerne deux méthodes couramment utilisées en inférence causale, l'une est DML avec une théorie statistique complète et l'autre est le modèle de réseau DR-Net et VC-Net. Ces méthodes ne peuvent traiter que des problèmes unidimensionnels, mais pour le problème de cet article, nous avons apporté quelques ajustements pour traiter des problèmes multidimensionnels, c'est-à-dire calculer d'abord la valeur absolue de chaque dimension, puis effectuer une normalisation. Il existe également des méthodes d'optimisation de stratégie dans les deux articles suivants, que nous appelons OPE et OCMD. Ces deux articles affirment que leurs méthodes sont adaptées à des problèmes multidimensionnels, mais ils soulignent également que lorsqu’il y a trop de dimensions, il est difficile pour ces méthodes d’être efficaces.

③ Ensemble de données de conception expérimentale-simulation
Afin de comparer les effets du modèle simplement et directement, nous avons simulé des problèmes du monde réel et généré une version simplifiée de l'ensemble de données de simulation. L'espace des fonctionnalités x représente 6 dimensions des fonctionnalités utilisateur et 2 fonctionnalités comportementales. Pour les échantillons présentant des caractéristiques différentes, nous supposons d’abord sa stratégie optimale. Comme le montre la figure, par exemple, un utilisateur âgé de moins de 45 ans, ayant un niveau d'éducation supérieur à 2 et une caractéristique comportementale supérieure à 0,5 est le meilleur dans 6 catégories de vidéos. À l'aide de la formule de gauche, générez d'abord aléatoirement une stratégie d'exposition pour l'utilisateur, puis calculez l'écart entre la stratégie d'exposition et la stratégie optimale réelle, ainsi que la durée de l'utilisateur simulé. Si la stratégie est plus proche de la stratégie optimale de l'utilisateur, la durée y de l'utilisateur sera plus longue. De cette façon, nous avons généré un tel ensemble de données. L'avantage de cet ensemble de données simulées est que nous supposons directement la valeur optimale, ce qui est très pratique pour l'évaluation. L'autre est que les données sont relativement simples, ce qui nous permet d'analyser plus facilement les résultats de l'algorithme.

Jetons un coup d'œil aux résultats expérimentaux sur l'ensemble de données simulées. Pour le type de personnes que nous venons de mentionner, diverses méthodes sont proposées pour calculer la valeur moyenne du traitement correspondant. La première ligne est l'optimal théorique, la deuxième ligne est notre forêt MDPP et la troisième ligne est basée sur la méthode forestière MDPP qui ajoute des termes de pénalité au critère de fractionnement. On voit que l’écart entre notre méthode et l’optimal théorique sera très faible. Les autres méthodes ne sont pas particulièrement extrêmes, mais relativement uniformes. De plus, d’après les chiffres MR et MTSE à droite, nos deux méthodes présentent également des avantages très évidents.

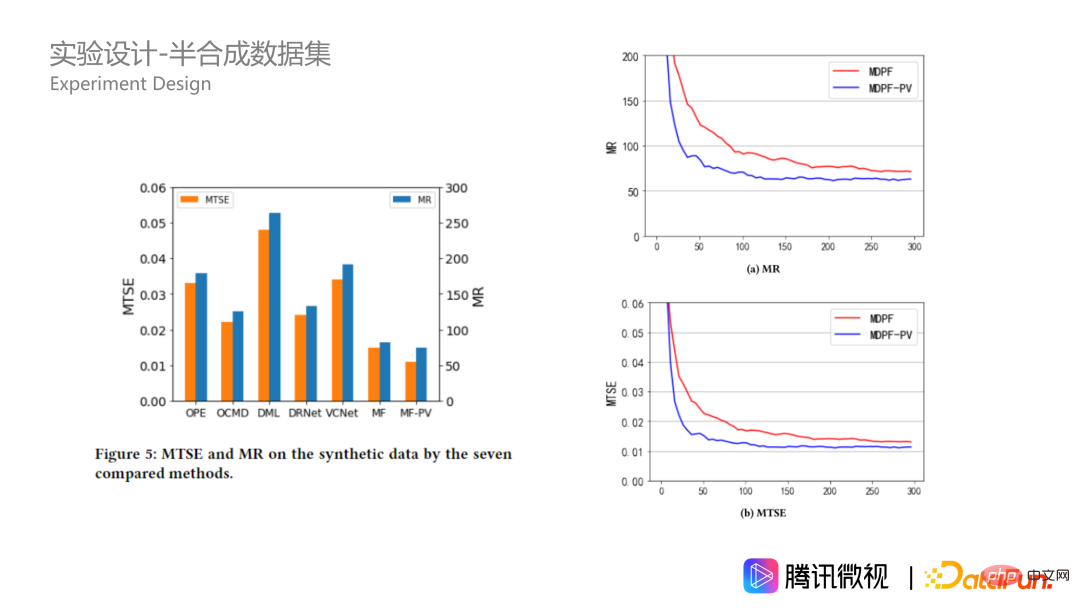
④ Conception expérimentale-ensemble de données semi-synthétiques
En plus de l'ensemble de données simulées, nous avons également construit des données semi-synthétiques basées sur des données commerciales réelles. Les données proviennent de la plateforme Tencent Weishi. Xi représente les caractéristiques à 20 dimensions de l'utilisateur, le traitement ti représente le rapport d'exposition de catégorie vidéo multidimensionnelle formant un vecteur à 10 dimensions, et yi(ti) représente la durée d'utilisation du i-ième utilisateur. Une caractéristique des scénarios réels est que nous ne pouvons pas connaître le taux d'exposition vidéo optimal réel de l'utilisateur. Par conséquent, nous construisons une fonction selon les règles du centre de cluster et générons y virtuel pour remplacer le y réel, afin que le y de l'échantillon ait une meilleure régularité. Je n’entrerai pas ici dans les détails de la formule spécifique. Les étudiants intéressés peuvent lire le texte original. Pourquoi est-ce possible ? Parce que la clé de notre algorithme est qu’il doit être capable de résoudre certains effets de confusion entre x et t, c’est-à-dire que les utilisateurs en ligne sont affectés par des stratégies biaisées. Afin d'évaluer l'effet de la stratégie, nous gardons uniquement x et t et modifions y pour mieux évaluer le problème.

Sur des données semi-synthétiques, notre algorithme est également nettement meilleur, et son avantage est encore plus grand que sur des jeux de données simulés. Cela montre que notre algorithme de forêts MDPP est plus stable lorsque les données sont complexes. Jetons également un coup d'œil aux hyperparamètres sur les données synthétiques, qui correspondent à la taille de la forêt. Dans l'image en bas à droite, nous pouvons voir qu'à mesure que la taille de la forêt augmente, les indicateurs convergent mieux sous les deux critères de fractionnement. Celui avec le terme de pénalité sera toujours meilleur, et il atteint mieux lorsqu'il y a 100 arbres. . L'effet optimal est obtenu avec 250 arbres, et il y aura alors un surajustement.
4. Séance de questions et réponses
Q : Pourquoi la normalisation peut-elle fonctionner lorsque l'exposition traversante dépasse 1 ?
A : Ma compréhension est la suivante, car ce que nous faisons est une optimisation avec des contraintes de proportion d'exposition. Dans ce processus, nous sommes une valeur relative. Au cours du processus de parcours, nous recherchons le point de partage optimal et déterminons quelle catégorie doit être prioritaire ainsi que la proportion d'exposition. Dans ce processus, tant que nous pouvons garantir que l’échelle est proportionnelle, tout va bien.
J'ai la même vue, il suffit de la mettre à l'échelle proportionnellement. Parce que 1 est une contrainte forte, la valeur que nous avons calculée au début ne sera certainement pas exactement 1, mais sera inférieure ou supérieure. S'il y en a beaucoup plus, il n'y a aucun moyen de le faire répondre à la condition unique de fortes contraintes, et il est plus naturel d'utiliser une pensée normalisée. Parce que nous considérons la relation de taille relative entre chaque catégorie. Je pense que la relation entre la taille relative est plus importante qu’une question de valeur absolue.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1657
1657
 14
14
 1415
1415
 52
52
 1309
1309
 25
25
 1257
1257
 29
29
 1231
1231
 24
24
 CLIP-BEVFormer : superviser explicitement la structure BEVFormer pour améliorer les performances de détection à longue traîne
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer : superviser explicitement la structure BEVFormer pour améliorer les performances de détection à longue traîne
Mar 26, 2024 pm 12:41 PM
Écrit ci-dessus et compréhension personnelle de l'auteur : À l'heure actuelle, dans l'ensemble du système de conduite autonome, le module de perception joue un rôle essentiel. Le véhicule autonome roulant sur la route ne peut obtenir des résultats de perception précis que via le module de perception en aval. dans le système de conduite autonome, prend des jugements et des décisions comportementales opportuns et corrects. Actuellement, les voitures dotées de fonctions de conduite autonome sont généralement équipées d'une variété de capteurs d'informations de données, notamment des capteurs de caméra à vision panoramique, des capteurs lidar et des capteurs radar à ondes millimétriques pour collecter des informations selon différentes modalités afin d'accomplir des tâches de perception précises. L'algorithme de perception BEV basé sur la vision pure est privilégié par l'industrie en raison de son faible coût matériel et de sa facilité de déploiement, et ses résultats peuvent être facilement appliqués à diverses tâches en aval.
 Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Les défis courants rencontrés par les algorithmes d'apprentissage automatique en C++ incluent la gestion de la mémoire, le multithread, l'optimisation des performances et la maintenabilité. Les solutions incluent l'utilisation de pointeurs intelligents, de bibliothèques de threads modernes, d'instructions SIMD et de bibliothèques tierces, ainsi que le respect des directives de style de codage et l'utilisation d'outils d'automatisation. Des cas pratiques montrent comment utiliser la bibliothèque Eigen pour implémenter des algorithmes de régression linéaire, gérer efficacement la mémoire et utiliser des opérations matricielles hautes performances.
 Explorez les principes sous-jacents et la sélection d'algorithmes de la fonction de tri C++
Apr 02, 2024 pm 05:36 PM
Explorez les principes sous-jacents et la sélection d'algorithmes de la fonction de tri C++
Apr 02, 2024 pm 05:36 PM
La couche inférieure de la fonction de tri C++ utilise le tri par fusion, sa complexité est O(nlogn) et propose différents choix d'algorithmes de tri, notamment le tri rapide, le tri par tas et le tri stable.
 L'intelligence artificielle peut-elle prédire la criminalité ? Explorez les capacités de CrimeGPT
Mar 22, 2024 pm 10:10 PM
L'intelligence artificielle peut-elle prédire la criminalité ? Explorez les capacités de CrimeGPT
Mar 22, 2024 pm 10:10 PM
La convergence de l’intelligence artificielle (IA) et des forces de l’ordre ouvre de nouvelles possibilités en matière de prévention et de détection de la criminalité. Les capacités prédictives de l’intelligence artificielle sont largement utilisées dans des systèmes tels que CrimeGPT (Crime Prediction Technology) pour prédire les activités criminelles. Cet article explore le potentiel de l’intelligence artificielle dans la prédiction de la criminalité, ses applications actuelles, les défis auxquels elle est confrontée et les éventuelles implications éthiques de cette technologie. Intelligence artificielle et prédiction de la criminalité : les bases CrimeGPT utilise des algorithmes d'apprentissage automatique pour analyser de grands ensembles de données, identifiant des modèles qui peuvent prédire où et quand les crimes sont susceptibles de se produire. Ces ensembles de données comprennent des statistiques historiques sur la criminalité, des informations démographiques, des indicateurs économiques, des tendances météorologiques, etc. En identifiant les tendances qui pourraient échapper aux analystes humains, l'intelligence artificielle peut donner du pouvoir aux forces de l'ordre.
 Algorithme de détection amélioré : pour la détection de cibles dans des images de télédétection optique haute résolution
Jun 06, 2024 pm 12:33 PM
Algorithme de détection amélioré : pour la détection de cibles dans des images de télédétection optique haute résolution
Jun 06, 2024 pm 12:33 PM
01Aperçu des perspectives Actuellement, il est difficile d'atteindre un équilibre approprié entre efficacité de détection et résultats de détection. Nous avons développé un algorithme YOLOv5 amélioré pour la détection de cibles dans des images de télédétection optique haute résolution, en utilisant des pyramides de caractéristiques multicouches, des stratégies de têtes de détection multiples et des modules d'attention hybrides pour améliorer l'effet du réseau de détection de cibles dans les images de télédétection optique. Selon l'ensemble de données SIMD, le mAP du nouvel algorithme est 2,2 % meilleur que YOLOv5 et 8,48 % meilleur que YOLOX, permettant ainsi d'obtenir un meilleur équilibre entre les résultats de détection et la vitesse. 02 Contexte et motivation Avec le développement rapide de la technologie de télédétection, les images de télédétection optique à haute résolution ont été utilisées pour décrire de nombreux objets à la surface de la Terre, notamment des avions, des voitures, des bâtiments, etc. Détection d'objets dans l'interprétation d'images de télédétection
 Pratique et réflexion sur la plateforme multimodale de grands modèles Jiuzhang Yunji DataCanvas
Oct 20, 2023 am 08:45 AM
Pratique et réflexion sur la plateforme multimodale de grands modèles Jiuzhang Yunji DataCanvas
Oct 20, 2023 am 08:45 AM
1. Le développement historique des grands modèles multimodaux. La photo ci-dessus est le premier atelier sur l'intelligence artificielle organisé au Dartmouth College aux États-Unis en 1956. Cette conférence est également considérée comme le coup d'envoi du développement de l'intelligence artificielle. pionniers de la logique symbolique (à l'exception du neurobiologiste Peter Milner au milieu du premier rang). Cependant, cette théorie de la logique symbolique n’a pas pu être réalisée avant longtemps et a même marqué le début du premier hiver de l’IA dans les années 1980 et 1990. Il a fallu attendre la récente mise en œuvre de grands modèles de langage pour découvrir que les réseaux de neurones portent réellement cette pensée logique. Les travaux du neurobiologiste Peter Milner ont inspiré le développement ultérieur des réseaux de neurones artificiels, et c'est pour cette raison qu'il a été invité à y participer. dans ce projet.
 Application d'algorithmes dans la construction de 58 plateformes de portraits
May 09, 2024 am 09:01 AM
Application d'algorithmes dans la construction de 58 plateformes de portraits
May 09, 2024 am 09:01 AM
1. Contexte de la construction de la plateforme 58 Portraits Tout d'abord, je voudrais partager avec vous le contexte de la construction de la plateforme 58 Portraits. 1. La pensée traditionnelle de la plate-forme de profilage traditionnelle ne suffit plus. La création d'une plate-forme de profilage des utilisateurs s'appuie sur des capacités de modélisation d'entrepôt de données pour intégrer les données de plusieurs secteurs d'activité afin de créer des portraits d'utilisateurs précis. Elle nécessite également l'exploration de données pour comprendre le comportement et les intérêts des utilisateurs. et besoins, et fournir des capacités côté algorithmes ; enfin, il doit également disposer de capacités de plate-forme de données pour stocker, interroger et partager efficacement les données de profil utilisateur et fournir des services de profil. La principale différence entre une plate-forme de profilage d'entreprise auto-construite et une plate-forme de profilage de middle-office est que la plate-forme de profilage auto-construite dessert un seul secteur d'activité et peut être personnalisée à la demande. La plate-forme de mid-office dessert plusieurs secteurs d'activité et est complexe ; modélisation et offre des fonctionnalités plus générales. 2.58 Portraits d'utilisateurs de l'arrière-plan de la construction du portrait sur la plate-forme médiane 58
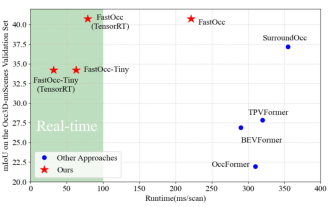 Ajoutez SOTA en temps réel et montez en flèche ! FastOcc : un algorithme Occ plus rapide et convivial pour le déploiement est là !
Mar 14, 2024 pm 11:50 PM
Ajoutez SOTA en temps réel et montez en flèche ! FastOcc : un algorithme Occ plus rapide et convivial pour le déploiement est là !
Mar 14, 2024 pm 11:50 PM
Écrit ci-dessus & La compréhension personnelle de l'auteur est que dans le système de conduite autonome, la tâche de perception est un élément crucial de l'ensemble du système de conduite autonome. L'objectif principal de la tâche de perception est de permettre aux véhicules autonomes de comprendre et de percevoir les éléments environnementaux environnants, tels que les véhicules circulant sur la route, les piétons au bord de la route, les obstacles rencontrés lors de la conduite, les panneaux de signalisation sur la route, etc., aidant ainsi en aval modules Prendre des décisions et des actions correctes et raisonnables. Un véhicule doté de capacités de conduite autonome est généralement équipé de différents types de capteurs de collecte d'informations, tels que des capteurs de caméra à vision panoramique, des capteurs lidar, des capteurs radar à ondes millimétriques, etc., pour garantir que le véhicule autonome peut percevoir et comprendre avec précision l'environnement environnant. éléments , permettant aux véhicules autonomes de prendre les bonnes décisions pendant la conduite autonome. Tête



