 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Apprentissage automatique quantique au-delà des méthodes du noyau, un cadre unifié pour les modèles d'apprentissage quantique
Apprentissage automatique quantique au-delà des méthodes du noyau, un cadre unifié pour les modèles d'apprentissage quantique
Apprentissage automatique quantique au-delà des méthodes du noyau, un cadre unifié pour les modèles d'apprentissage quantique
Les algorithmes d'apprentissage automatique basés sur des circuits quantiques paramétrés sont des candidats privilégiés pour des applications à court terme sur des ordinateurs quantiques bruyants. Dans cette direction, divers types de modèles d’apprentissage automatique quantique ont été introduits et étudiés de manière approfondie. Cependant, notre compréhension de la manière dont ces modèles se comparent entre eux et aux modèles classiques reste limitée.
Récemment, une équipe de recherche de l'Université d'Innsbruck, en Autriche, a identifié un cadre constructif qui capture tous les modèles standards basés sur des circuits quantiques paramétrés : le modèle quantique linéaire.
Les chercheurs montrent comment utiliser les outils de la théorie de l'information quantique pour cartographier efficacement les circuits de ré-téléchargement de données en une image plus simple d'un modèle linéaire dans l'espace quantique de Hilbert. De plus, les besoins en ressources expérimentalement pertinents de ces modèles sont analysés en termes de nombre de qubits et de quantité de données à apprendre. Des résultats récents basés sur l'apprentissage automatique classique démontrent que les modèles quantiques linéaires doivent utiliser beaucoup plus de qubits que les modèles de rechargement de données pour résoudre certaines tâches d'apprentissage, tandis que les méthodes du noyau nécessitent également beaucoup plus de points de données. Les résultats fournissent une compréhension plus complète des modèles d’apprentissage automatique quantique, ainsi que des informations sur la compatibilité des différents modèles avec les contraintes NISQ.
La recherche était intitulée « Apprentissage automatique quantique au-delà des méthodes du noyau » et a été publiée dans « Nature Communications » le 31 janvier 2023.
Lien papier : https://www.nature.co m/articles/s41467-023-36159-y
Intermédiaire Quantique (NISQ) À cette époque, plusieurs méthodes ont été proposées pour construire des algorithmes quantiques utiles compatibles avec de légères contraintes matérielles. La plupart de ces méthodes impliquent la spécification de circuits quantiques Ansatz, optimisés de manière classique pour résoudre des tâches de calcul spécifiques. Outre les solveurs de signature quantique variationnelle et les variantes d’algorithmes d’optimisation quantique approximative en chimie, les méthodes d’apprentissage automatique basées sur de tels circuits quantiques paramétrés constituent l’une des applications pratiques les plus prometteuses pour générer des avantages quantiques.
Les méthodes du noyau sont un type d'algorithme de reconnaissance de formes. Son objectif est de trouver et d'apprendre les relations mutuelles dans un ensemble de données. La méthode du noyau est un moyen efficace de résoudre les problèmes d'analyse de modèles non linéaires. Son idée principale est la suivante : premièrement, intégrer les données originales dans un espace de fonctionnalités de haute dimension approprié via un mappage non linéaire, puis utiliser un apprenant linéaire général pour de nouveaux modes d'analyse ; et le traitement dans l'espace.
Des travaux antérieurs ont fait de grands progrès dans cette direction en exploitant la connexion entre certains modèles quantiques et les méthodes du noyau de l'apprentissage automatique classique. De nombreux modèles quantiques fonctionnent en effet en codant les données dans un espace de Hilbert de grande dimension et en modélisant les propriétés des données en utilisant uniquement des produits internes évalués dans cet espace de fonctionnalités. C’est aussi ainsi que fonctionne la méthode nucléaire.
Sur la base de cette similarité, un codage quantique donné peut être utilisé pour définir deux types de modèles : (a) des modèles quantiques explicites, où les points de données de codage sont mesurés en fonction d'observables variationnels qui spécifient leurs étiquettes ; Modèle de noyau implicite, dans lequel un produit interne pondéré de points de données codés est utilisé pour attribuer des étiquettes. Dans la littérature sur l’apprentissage automatique quantique, l’accent est mis sur les modèles implicites.
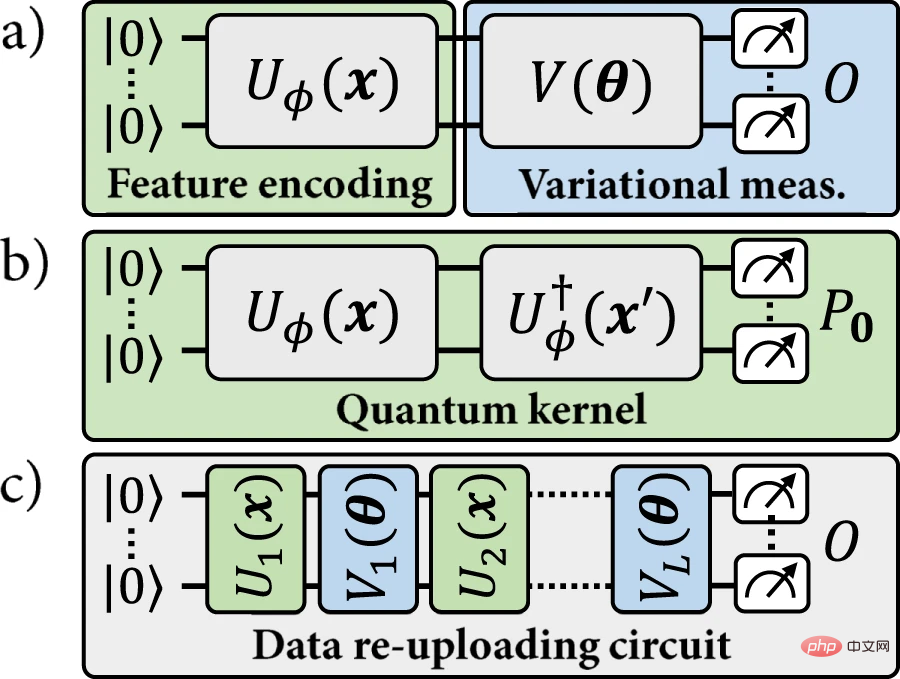
Figure 1 : Le modèle d'apprentissage automatique quantique étudié dans ce travail. (Source : article)
Récemment, des progrès ont été réalisés dans les modèles dits de ré-téléchargement de données. Le modèle de ré-téléchargement des données peut être considéré comme une généralisation du modèle explicite. Cependant, cette généralisation rompt également la correspondance avec le modèle implicite, puisqu'un point de donnée x donné ne correspond plus à un point de codage fixe ρ(x). Les modèles de réupload de données sont strictement plus généraux que les modèles explicites et ne sont pas compatibles avec le paradigme du modèle du noyau. Jusqu'à présent, la question reste ouverte de savoir si certains avantages peuvent être obtenus à partir des modèles de ré-téléchargement de données avec la garantie des méthodes du noyau.
Dans ce travail, les chercheurs introduisent un cadre unifié pour les modèles quantiques explicites, implicites et de ré-upload de données.
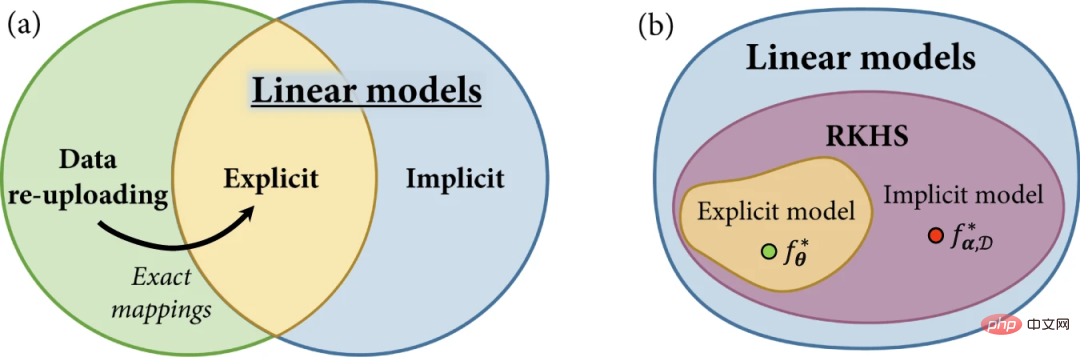
Figure 2 : Famille de modèles en apprentissage automatique quantique. (Source : article)
Cadre unifié pour les modèles d'apprentissage quantique
Commencez par revoir le concept de modèles quantiques linéaires et en expliquant les modèles explicites et implicites en termes de modèles linéaires définis dans l'espace des fonctionnalités quantiques. Ensuite, des modèles de rechargement de données sont présentés et montrent que, bien que définis comme des généralisations de modèles explicites, ils peuvent également être implémentés par des modèles linéaires dans des espaces de Hilbert plus grands.
Modèle quantique linéaire
La figure ci-dessous donne une structure illustrative pour illustrer visuellement comment le mappage du nouveau téléchargement des données au modèle explicite est réalisé.
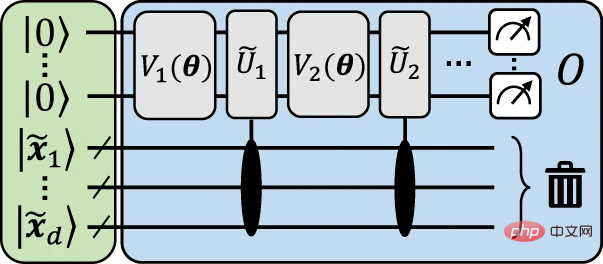
Figure 3 : Modèle explicite illustratif se rapprochant du circuit de ré-upload de données. (Source : Paper)
L'idée générale derrière cette structure est d'encoder les données d'entrée.
Passons maintenant à la structure principale, ce qui entraîne un nouveau téléchargement des données et un mappage précis entre les modèles explicites. Ici, en s'appuyant sur une idée similaire à la structure précédente, les données d'entrée sont codées sur le qubit auxiliaire, puis la porte de codage est implémentée sur le qubit de travail à l'aide d'opérations indépendantes des données. La différence ici est d'utiliser la téléportation de porte, un type d'informatique quantique basée sur des mesures, pour implémenter des portes de codage directement sur les qubits auxiliaires et les téléporter (via des mesures d'intrication) vers les qubits de travail lorsque cela est nécessaire.
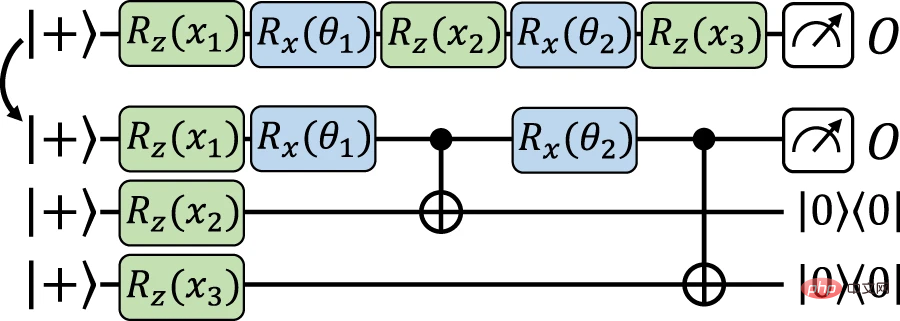
Figure 4 : Cartographie exacte du modèle de retéléchargement de données vers un modèle explicite équivalent utilisant la téléportation fermée. (Source : article)
Les chercheurs ont démontré que les modèles quantiques linéaires peuvent décrire non seulement des modèles explicites et implicites, mais également des circuits de rechargement de données. Plus précisément, toute classe d'hypothèses de modèles de réupload de données peut être mappée à une classe équivalente de modèles explicites, c'est-à-dire des modèles linéaires avec une famille restreinte d'observables.
Ensuite, les chercheurs ont analysé plus rigoureusement les avantages des modèles explicites et de ré-téléchargement de données par rapport aux modèles implicites. Dans l'exemple, l'efficacité du modèle quantique dans la résolution de la tâche d'apprentissage est quantifiée par le nombre de qubits et la taille de l'ensemble d'apprentissage requis pour obtenir une perte attendue non triviale. La tâche d’apprentissage qui nous intéresse consiste à apprendre les fonctions paires et impaires.
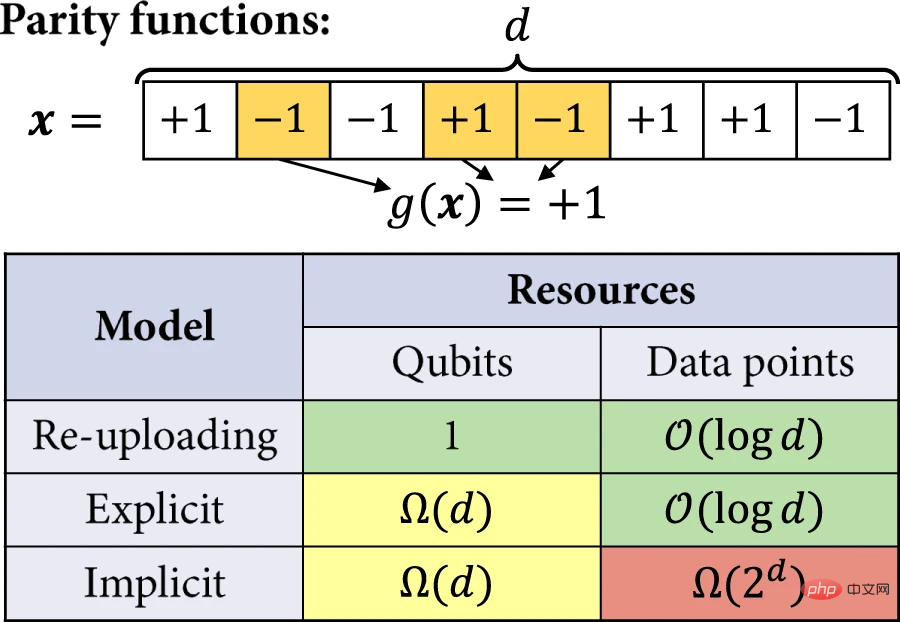
Figure 5 : Apprendre à se séparer. (Source : article)
Avantages quantiques au-delà des méthodes du noyau
Un défi majeur dans l'apprentissage automatique quantique est de montrer que les méthodes quantiques discutées dans cet ouvrage peuvent offrir des avantages d'apprentissage par rapport aux méthodes classiques (standard).
Dans cette recherche, Huang et al. de Google Quantum Artificial Intelligence (https://www.php.cn/link/4dfd2a142d36707f8043c40ce0746761 ) Il est recommandé d'étudier les tâches d'apprentissage dans lesquelles la fonction objectif elle-même est générée par des modèles quantiques (explicites).
Semblable à Huang et al., les chercheurs ont effectué la tâche de régression en utilisant les données d'entrée de l'ensemble de données fashion-MNIST, où chaque exemple était une image en niveaux de gris de 28 x 28.
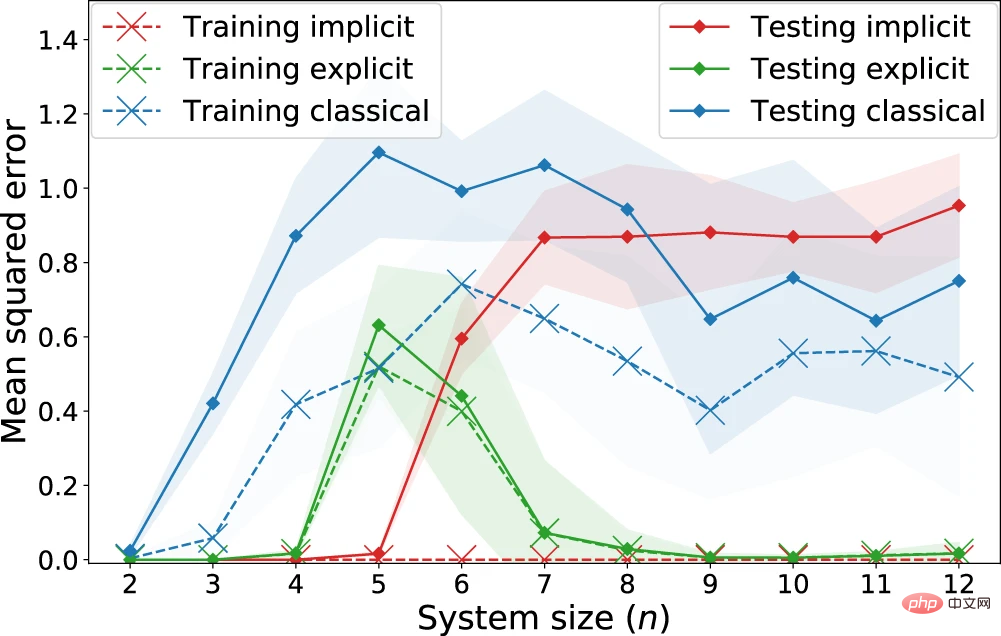
Figure 6 : Performance de régression de modèles explicites, implicites et classiques sur la tâche d'apprentissage "personnalisation quantique". (Source : Papier)
Observé : Les modèles implicites obtiennent systématiquement des pertes d'entraînement inférieures aux modèles explicites. Surtout pour les pertes non régularisées, le modèle implicite atteint une perte d’entraînement de 0. En revanche, en ce qui concerne les pertes de test qui représentent les pertes attendues, il existe une séparation nette à partir de n = 7 qubits, où le modèle classique commence à avoir des performances compétitives avec le modèle implicite, tandis que le modèle explicite les surpasse clairement tous les deux. . Cela suggère que la présence d’un avantage quantique ne doit pas être évaluée uniquement en comparant les modèles classiques avec les méthodes du noyau quantique, car les modèles explicites (ou de ré-téléchargement de données) peuvent également cacher de meilleures performances d’apprentissage.
Ces résultats nous donnent une compréhension plus complète du domaine de l'apprentissage automatique quantique et élargissent notre vision des types de modèles permettant d'obtenir des avantages d'apprentissage pratiques dans les mécanismes NISQ.
Les chercheurs estiment que la tâche d'apprentissage visant à prouver l'existence d'une séparation exponentielle d'apprentissage entre différents modèles quantiques est basée sur des fonctions paires et impaires, ce qui n'est pas une classe conceptuelle d'intérêt pratique pour l'apprentissage automatique. Cependant, les résultats de la limite inférieure peuvent également être étendus à d’autres tâches d’apprentissage avec des classes de concepts de grande dimension (c’est-à-dire constituées de nombreuses fonctions orthogonales).
Les méthodes du noyau quantique nécessitent nécessairement de nombreux points de données qui évoluent linéairement avec cette dimension, et comme nous le montrons dans les résultats, la flexibilité du circuit de ré-téléchargement des données et les capacités d'expression limitées du modèle explicite permettent d'économiser des ressources importantes. Explorer comment et quand ces modèles peuvent être adaptés à la tâche d’apprentissage automatique à accomplir reste une direction de recherche intéressante.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Utilisez ddrescue pour récupérer des données sous Linux
Mar 20, 2024 pm 01:37 PM
Utilisez ddrescue pour récupérer des données sous Linux
Mar 20, 2024 pm 01:37 PM
DDREASE est un outil permettant de récupérer des données à partir de périphériques de fichiers ou de blocs tels que des disques durs, des SSD, des disques RAM, des CD, des DVD et des périphériques de stockage USB. Il copie les données d'un périphérique bloc à un autre, laissant derrière lui les blocs corrompus et ne déplaçant que les bons blocs. ddreasue est un puissant outil de récupération entièrement automatisé car il ne nécessite aucune interruption pendant les opérations de récupération. De plus, grâce au fichier map ddasue, il peut être arrêté et repris à tout moment. Les autres fonctionnalités clés de DDREASE sont les suivantes : Il n'écrase pas les données récupérées mais comble les lacunes en cas de récupération itérative. Cependant, il peut être tronqué si l'outil est invité à le faire explicitement. Récupérer les données de plusieurs fichiers ou blocs en un seul
 Open source! Au-delà de ZoeDepth ! DepthFM : estimation rapide et précise de la profondeur monoculaire !
Apr 03, 2024 pm 12:04 PM
Open source! Au-delà de ZoeDepth ! DepthFM : estimation rapide et précise de la profondeur monoculaire !
Apr 03, 2024 pm 12:04 PM
0. À quoi sert cet article ? Nous proposons DepthFM : un modèle d'estimation de profondeur monoculaire génératif de pointe, polyvalent et rapide. En plus des tâches traditionnelles d'estimation de la profondeur, DepthFM démontre également des capacités de pointe dans les tâches en aval telles que l'inpainting en profondeur. DepthFM est efficace et peut synthétiser des cartes de profondeur en quelques étapes d'inférence. Lisons ce travail ensemble ~ 1. Titre des informations sur l'article : DepthFM : FastMonocularDepthEstimationwithFlowMatching Auteur : MingGui, JohannesS.Fischer, UlrichPrestel, PingchuanMa, Dmytr
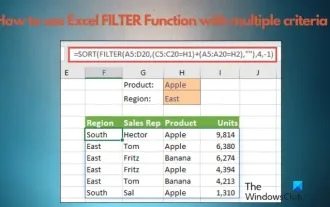 Comment utiliser la fonction de filtre Excel avec plusieurs conditions
Feb 26, 2024 am 10:19 AM
Comment utiliser la fonction de filtre Excel avec plusieurs conditions
Feb 26, 2024 am 10:19 AM
Si vous avez besoin de savoir comment utiliser le filtrage avec plusieurs critères dans Excel, le didacticiel suivant vous guidera à travers les étapes pour vous assurer que vous pouvez filtrer et trier efficacement vos données. La fonction de filtrage d'Excel est très puissante et peut vous aider à extraire les informations dont vous avez besoin à partir de grandes quantités de données. Cette fonction peut filtrer les données en fonction des conditions que vous définissez et afficher uniquement les pièces qui remplissent les conditions, rendant la gestion des données plus efficace. En utilisant la fonction de filtre, vous pouvez trouver rapidement des données cibles, ce qui vous fait gagner du temps dans la recherche et l'organisation des données. Cette fonction peut non seulement être appliquée à de simples listes de données, mais peut également être filtrée en fonction de plusieurs conditions pour vous aider à localiser plus précisément les informations dont vous avez besoin. Dans l’ensemble, la fonction de filtrage d’Excel est très utile
 Google est ravi : les performances de JAX surpassent Pytorch et TensorFlow ! Cela pourrait devenir le choix le plus rapide pour la formation à l'inférence GPU
Apr 01, 2024 pm 07:46 PM
Google est ravi : les performances de JAX surpassent Pytorch et TensorFlow ! Cela pourrait devenir le choix le plus rapide pour la formation à l'inférence GPU
Apr 01, 2024 pm 07:46 PM
Les performances de JAX, promu par Google, ont dépassé celles de Pytorch et TensorFlow lors de récents tests de référence, se classant au premier rang sur 7 indicateurs. Et le test n’a pas été fait sur le TPU présentant les meilleures performances JAX. Bien que parmi les développeurs, Pytorch soit toujours plus populaire que Tensorflow. Mais à l’avenir, des modèles plus volumineux seront peut-être formés et exécutés sur la base de la plate-forme JAX. Modèles Récemment, l'équipe Keras a comparé trois backends (TensorFlow, JAX, PyTorch) avec l'implémentation native de PyTorch et Keras2 avec TensorFlow. Premièrement, ils sélectionnent un ensemble de
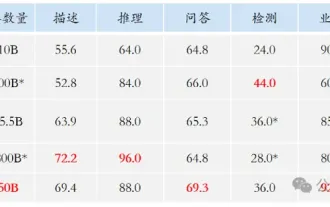 La vitalité de la super intelligence s'éveille ! Mais avec l'arrivée de l'IA qui se met à jour automatiquement, les mères n'ont plus à se soucier des goulots d'étranglement des données.
Apr 29, 2024 pm 06:55 PM
La vitalité de la super intelligence s'éveille ! Mais avec l'arrivée de l'IA qui se met à jour automatiquement, les mères n'ont plus à se soucier des goulots d'étranglement des données.
Apr 29, 2024 pm 06:55 PM
Je pleure à mort. Le monde construit à la folie de grands modèles. Les données sur Internet ne suffisent pas du tout. Le modèle de formation ressemble à « The Hunger Games », et les chercheurs en IA du monde entier se demandent comment nourrir ces personnes avides de données. Ce problème est particulièrement important dans les tâches multimodales. À une époque où rien ne pouvait être fait, une équipe de start-up du département de l'Université Renmin de Chine a utilisé son propre nouveau modèle pour devenir la première en Chine à faire de « l'auto-alimentation des données générées par le modèle » une réalité. De plus, il s’agit d’une approche à deux volets, du côté compréhension et du côté génération, les deux côtés peuvent générer de nouvelles données multimodales de haute qualité et fournir un retour de données au modèle lui-même. Qu'est-ce qu'un modèle ? Awaker 1.0, un grand modèle multimodal qui vient d'apparaître sur le Forum Zhongguancun. Qui est l'équipe ? Moteur Sophon. Fondé par Gao Yizhao, doctorant à la Hillhouse School of Artificial Intelligence de l’Université Renmin.
 Vitesse Internet lente des données cellulaires sur iPhone : correctifs
May 03, 2024 pm 09:01 PM
Vitesse Internet lente des données cellulaires sur iPhone : correctifs
May 03, 2024 pm 09:01 PM
Vous êtes confronté à un décalage et à une connexion de données mobile lente sur iPhone ? En règle générale, la puissance de l'Internet cellulaire sur votre téléphone dépend de plusieurs facteurs tels que la région, le type de réseau cellulaire, le type d'itinérance, etc. Vous pouvez prendre certaines mesures pour obtenir une connexion Internet cellulaire plus rapide et plus fiable. Correctif 1 – Forcer le redémarrage de l'iPhone Parfois, le redémarrage forcé de votre appareil réinitialise simplement beaucoup de choses, y compris la connexion cellulaire. Étape 1 – Appuyez simplement une fois sur la touche d’augmentation du volume et relâchez-la. Ensuite, appuyez sur la touche de réduction du volume et relâchez-la à nouveau. Étape 2 – La partie suivante du processus consiste à maintenir le bouton sur le côté droit. Laissez l'iPhone finir de redémarrer. Activez les données cellulaires et vérifiez la vitesse du réseau. Vérifiez à nouveau Correctif 2 – Changer le mode de données Bien que la 5G offre de meilleures vitesses de réseau, elle fonctionne mieux lorsque le signal est plus faible
 L'US Air Force présente son premier avion de combat IA de grande envergure ! Le ministre a personnellement effectué l'essai routier sans intervenir pendant tout le processus, et 100 000 lignes de code ont été testées 21 fois.
May 07, 2024 pm 05:00 PM
L'US Air Force présente son premier avion de combat IA de grande envergure ! Le ministre a personnellement effectué l'essai routier sans intervenir pendant tout le processus, et 100 000 lignes de code ont été testées 21 fois.
May 07, 2024 pm 05:00 PM
Récemment, le milieu militaire a été submergé par la nouvelle : les avions de combat militaires américains peuvent désormais mener des combats aériens entièrement automatiques grâce à l'IA. Oui, tout récemment, l’avion de combat IA de l’armée américaine a été rendu public pour la première fois, dévoilant ainsi son mystère. Le nom complet de ce chasseur est Variable Stability Simulator Test Aircraft (VISTA). Il a été personnellement piloté par le secrétaire de l'US Air Force pour simuler une bataille aérienne en tête-à-tête. Le 2 mai, le secrétaire de l'US Air Force, Frank Kendall, a décollé à bord d'un X-62AVISTA à la base aérienne d'Edwards. Notez que pendant le vol d'une heure, toutes les actions de vol ont été effectuées de manière autonome par l'IA ! Kendall a déclaré : "Au cours des dernières décennies, nous avons réfléchi au potentiel illimité du combat air-air autonome, mais cela a toujours semblé hors de portée." Mais maintenant,
 Le premier robot capable d'accomplir de manière autonome des tâches humaines apparaît, avec cinq doigts flexibles et rapides, et de grands modèles prennent en charge l'entraînement dans l'espace virtuel
Mar 11, 2024 pm 12:10 PM
Le premier robot capable d'accomplir de manière autonome des tâches humaines apparaît, avec cinq doigts flexibles et rapides, et de grands modèles prennent en charge l'entraînement dans l'espace virtuel
Mar 11, 2024 pm 12:10 PM
Cette semaine, FigureAI, une entreprise de robotique investie par OpenAI, Microsoft, Bezos et Nvidia, a annoncé avoir reçu près de 700 millions de dollars de financement et prévoit de développer un robot humanoïde capable de marcher de manière autonome au cours de la prochaine année. Et l’Optimus Prime de Tesla a reçu à plusieurs reprises de bonnes nouvelles. Personne ne doute que cette année sera celle de l’explosion des robots humanoïdes. SanctuaryAI, une entreprise canadienne de robotique, a récemment lancé un nouveau robot humanoïde, Phoenix. Les responsables affirment qu’il peut accomplir de nombreuses tâches de manière autonome, à la même vitesse que les humains. Pheonix, le premier robot au monde capable d'accomplir des tâches de manière autonome à la vitesse d'un humain, peut saisir, déplacer et placer avec élégance chaque objet sur ses côtés gauche et droit. Il peut identifier des objets de manière autonome





