Écrivez un programme capable de dessiner un triangle équilatéral, et de chaque côté du triangle, il doit être capable de dessiner un triangle légèrement plus petit orienté vers l'extérieur. Pouvoir répéter ce processus autant de fois que l’on le souhaite crée des modèles intéressants.
Représenter l'image sous la forme d'un tableau de pixels bidimensionnel. Chaque cellule du tableau de pixels représentera la couleur (RVB) de ce pixel.
Pour ce faire, vous pouvez utiliser la bibliothèque NumPy pour générer un tableau de pixels et Pillow pour le convertir en une image pouvant être enregistrée.
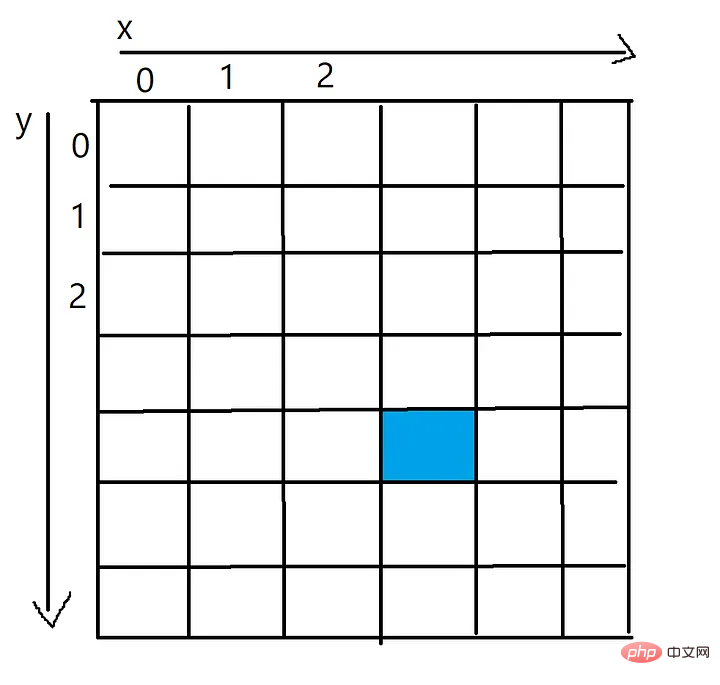
La valeur x du pixel bleu est 3 et la valeur y est 4, accessible via un tableau bidimensionnel, tel que les pixels[4][3]
Maintenant, commencez à coder, vous avez d'abord besoin d'une fonction qui peut prendre deux ensembles de coordonnées et tracer une ligne entre eux.
Le code ci-dessous fonctionne par interpolation entre deux points, ajoutant de nouveaux pixels au tableau de pixels à chaque étape. Vous pouvez considérer ce processus comme un ombrage pixel par pixel sur une ligne.
Vous pouvez utiliser le caractère continu "" dans chaque extrait de code pour accueillir des lignes de code plus longues.
import numpy as np
from PIL import Image
import math
def plot_line(from_coordinates, to_coordinates, thickness, colour, pixels):
# 找出像素阵列的边界
max_x_coordinate = len(pixels[0])
max_y_coordinate = len(pixels)
# 两点之间沿着x轴和y轴的距离
horizontal_distance = to_coordinates[1] - from_coordinates[1]
vertical_distance = to_coordinates[0] - from_coordinates[0]
# 两点之间的总距离
distance = math.sqrt((to_coordinates[1] - from_coordinates[1])**2 \
+ (to_coordinates[0] - from_coordinates[0])**2)
# 每次给一个新的像素上色时，将向前走多远
horizontal_step = horizontal_distance/distance
vertical_step = vertical_distance/distance
# 此时，将进入循环以在像素数组中绘制线
# 循环的每一次迭代都会沿着线添加一个新的点
for i in range(round(distance)):
# 这两个坐标是直线中心的坐标
current_x_coordinate = round(from_coordinates[1] + (horizontal_step*i))
current_y_coordinate = round(from_coordinates[0] + (vertical_step*i))
# 一旦得到了点的坐标，
# 就在坐标周围画出尺寸为thickness的图案
for x in range (-thickness, thickness):
for y in range (-thickness, thickness):
x_value = current_x_coordinate + x
y_value = current_y_coordinate + y
if (x_value > 0 and x_value < max_x_coordinate and \
y_value > 0 and y_value < max_y_coordinate):
pixels[y_value][x_value] = colour
# 定义图像的大小
pixels = np.zeros( (500,500,3), dtype=np.uint8 )
# 画一条线
plot_line([0,0], [499,499], 1, [255,200,0], pixels)
# 把像素阵列变成一张真正的图片
img = Image.fromarray(pixels)
# 显示得到的图片，并保存它
img.show()
img.save('Line.png')
Le résultat de cette fonction lors du tracé d'une ligne jaune entre chaque coin du tableau de pixels
Maintenant qu'il existe une fonction qui peut tracer une ligne entre deux points, vous pouvez dessiner le troisième Un triangle équilatéral.
Étant donné le point central et la longueur des côtés d'un triangle, la hauteur peut être calculée à l'aide de la formule : h = ½(√3a).
Maintenant, en utilisant cette hauteur, ce point central et ces longueurs de côtés, vous pouvez calculer la position de chaque coin du triangle. En utilisant la fonction plot_line que nous avons créée précédemment, nous pouvons tracer une ligne entre chaque coin. plot_line函数，可以在每个角之间画一条线。
def draw_triangle(center, side_length, thickness, colour, pixels):
# 等边三角形的高度是，h = ½(√3a)
# 其中a是边长
triangle_height = round(side_length * math.sqrt(3)/2)
# 顶角
top = [center[0] - triangle_height/2, center[1]]
# 左下角
bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2]
# 右下角
bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2]
# 在每个角之间画一条线来完成三角形
plot_line(top, bottom_left, thickness, colour, pixels)
plot_line(top, bottom_right, thickness, colour, pixels)
plot_line(bottom_left, bottom_right, thickness, colour, pixels)
在500x500像素PNG的中心绘制三角形时的结果
一切都已准备就绪，可以用Python创建第一个分形。
但是最后一步是最难完成的，三角形函数为它的每一边调用自己，需要能够计算每个新的较小三角形的中心点，并正确地旋转它们，使它们垂直于它们所附着的一侧。
通过从旋转的坐标中减去中心点的偏移量，然后应用公式来旋转一对坐标，可以用这个函数来旋转三角形的每个角。
def rotate(coordinate, center_point, degrees):
# 从坐标中减去旋转的点
x = (coordinate[0] - center_point[0])
y = (coordinate[1] - center_point[1])
# Python的cos和sin函数采用弧度而不是度数
radians = math.radians(degrees)
# 计算旋转点
new_x = (x * math.cos(radians)) - (y * math.sin(radians))
new_y = (y * math.cos(radians)) + (x * math.sin(radians))
# 将在开始时减去的偏移量加回旋转点上
return [new_x + center_point[0], new_y + center_point[1]]
将每个坐标旋转35度的三角形
可以旋转一个三角形后，思考如何在第一个三角形的每条边上画一个新的小三角形。
为了实现这一点，扩展draw_triangle函数，为每条边计算一个新三角形的旋转和中心点，其边长被参数shrink_side_by减少。
一旦它计算出新三角形的中心点和旋转，它就会调用draw_triangle（自身）来从当前线的中心画出新的、更小的三角形。然后，这将反过来打击同一个代码块，为一个更小的三角形计算另一组中心点和旋转。
这就是所谓的循环算法，因为draw_triangle
def draw_triangle(center, side_length, degrees_rotate, thickness, colour, \
pixels, shrink_side_by, iteration, max_depth):
# 等边三角形的高度是，h = ½(√3a)
# 其中'a'是边长
triangle_height = side_length * math.sqrt(3)/2
# 顶角
top = [center[0] - triangle_height/2, center[1]]
# 左下角
bottom_left = [center[0] + triangle_height/2, center[1] - side_length/2]
# 右下角
bottom_right = [center[0] + triangle_height/2, center[1] + side_length/2]
if (degrees_rotate != 0):
top = rotate(top, center, degrees_rotate)
bottom_left = rotate(bottom_left, center, degrees_rotate)
bottom_right = rotate(bottom_right, center, degrees_rotate)
# 三角形各边之间的坐标
lines = [[top, bottom_left],[top, bottom_right],[bottom_left, bottom_right]]
line_number = 0
# 在每个角之间画一条线来完成三角形
for line in lines:
line_number += 1
plot_line(line[0], line[1], thickness, colour, pixels)
# 如果还没有达到max_depth，就画一些新的三角形
if (iteration < max_depth and (iteration < 1 or line_number < 3)):
gradient = (line[1][0] - line[0][0]) / (line[1][1] - line[0][1])
new_side_length = side_length*shrink_side_by
# 正在绘制的三角形线的中心
center_of_line = [(line[0][0] + line[1][0]) / 2, \
(line[0][1] + line[1][1]) / 2]
new_center = []
new_rotation = degrees_rotate
# 需要旋转traingle的数量
if (line_number == 1):
new_rotation += 60
elif (line_number == 2):
new_rotation -= 60
else:
new_rotation += 180
# 在一个理想的世界里，这将是gradient=0，
# 但由于浮点除法的原因，无法
# 确保永远是这种情况
if (gradient < 0.0001 and gradient > -0.0001):
if (center_of_line[0] - center[0] > 0):
new_center = [center_of_line[0] + triangle_height * \
(shrink_side_by/2), center_of_line[1]]
else:
new_center = [center_of_line[0] - triangle_height * \
(shrink_side_by/2), center_of_line[1]]
else:
# 计算直线梯度的法线
difference_from_center = -1/gradient
# 计算这条线距中心的距离
# 到新三角形的中心
distance_from_center = triangle_height * (shrink_side_by/2)
# 计算 x 方向的长度，
# 从线的中心到新三角形的中心
x_length = math.sqrt((distance_from_center**2)/ \
(1 + difference_from_center**2))
# 计算出x方向需要走哪条路
if (center_of_line[1] < center[1] and x_length > 0):
x_length *= -1
# 现在计算Y方向的长度
y_length = x_length * difference_from_center
# 用新的x和y值来偏移线的中心
new_center = [center_of_line[0] + y_length, \
center_of_line[1] + x_length]
draw_triangle(new_center, new_side_length, new_rotation, \
thickness, colour, pixels, shrink_side_by, \
iteration+1, max_depth)
en 500x500 pixels PNG Le résultat en dessinant un triangle au centre
5. Générer une fractale
🎜 Tout est prêt pour créer la première fractale en Python. 🎜🎜Mais la dernière étape est la plus difficile à réaliser, la fonction triangle s'appelle pour chaque côté de celui-ci, il faut pouvoir calculer le point central de chaque nouveau triangle plus petit et les faire pivoter correctement pour qu'ils soient perpendiculaires à celui-ci. ils sont attachés à côté. 🎜🎜Vous pouvez utiliser cette fonction pour faire pivoter chaque coin d'un triangle en soustrayant le décalage du point central des coordonnées pivotées, puis en appliquant la formule pour faire pivoter une paire de coordonnées. 🎜rrreee🎜🎜🎜Convertir chacun coordonner Faites pivoter un triangle de 35 degrés🎜🎜Après avoir fait pivoter un triangle, réfléchissez à la façon de dessiner un nouveau petit triangle de chaque côté du premier triangle. 🎜🎜Pour y parvenir, étendez la fonction draw_triangle pour calculer la rotation et le point central d'un nouveau triangle pour chaque côté, dont les longueurs des côtés sont réduites par le paramètre shrink_side_by. 🎜🎜Une fois qu'il a calculé le point central et la rotation du nouveau triangle, il appelle draw_triangle(self) pour dessiner le nouveau triangle plus petit à partir du centre de la ligne actuelle. Cela frappera ensuite le même bloc de code à l'envers pour calculer un autre ensemble de points centraux et de rotations pour un triangle plus petit. 🎜🎜C'est ce qu'on appelle un algorithme de boucle car la fonction draw_triangle s'appelle désormais jusqu'à ce qu'elle atteigne la profondeur maximale du triangle qu'elle souhaite dessiner. Avoir cette phrase d'échappement est important car en théorie la fonction bouclerait indéfiniment (mais en pratique la pile d'appels deviendrait trop volumineuse, provoquant une erreur de débordement de pile). 🎜rrreee🎜🎜🎜🎜Fractale triangulaire, côtés rétrécissants = 1/2, profondeur maximale = 2🎜Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
