
Alors avant de commencer, parlons de l'algorithme PSO de base. Le noyau n'en est qu'un :

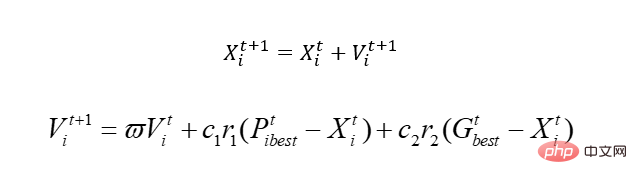
Expliquez-nous cette formule, et vous comprendrez.
Anciennes règles, nous supposons qu'il existe une équation y=sin(x1)+cos(x2)
L'algorithme PSO réalise notre optimisation en simulant la migration des oiseaux. Comment cela se produit-il. ? Oui, je n'entrerai pas dans les détails, mais parlons du fond.
Dans l'équation que nous venons d'avoir, il y a deux variables, x1 et x2. Parce qu'il s'agit d'un oiseau simulé, afin de réaliser la méthode aveugle, le concept de vitesse est introduit ici. X est naturellement notre domaine réalisable, qui est l'espace des solutions. En modifiant la vitesse, x est déplacé, c'est-à-dire que la valeur de x est modifiée. Parmi eux, Pbest représente la solution optimale pour l’endroit où l’oiseau a marché, et Gbest représente la solution optimale pour l’ensemble de la population. Que voulez-vous dire, c'est-à-dire qu'à mesure qu'il bouge, cet oiseau peut se déplacer vers une position pire, car contrairement à la génétique, il sera tué s'il est mauvais, mais celui-ci ne le sera pas. Bien entendu, de nombreux problèmes locaux sont impliqués, dont nous ne discuterons pas ici. Aucun algorithme n’est parfait, et celui-ci est juste.
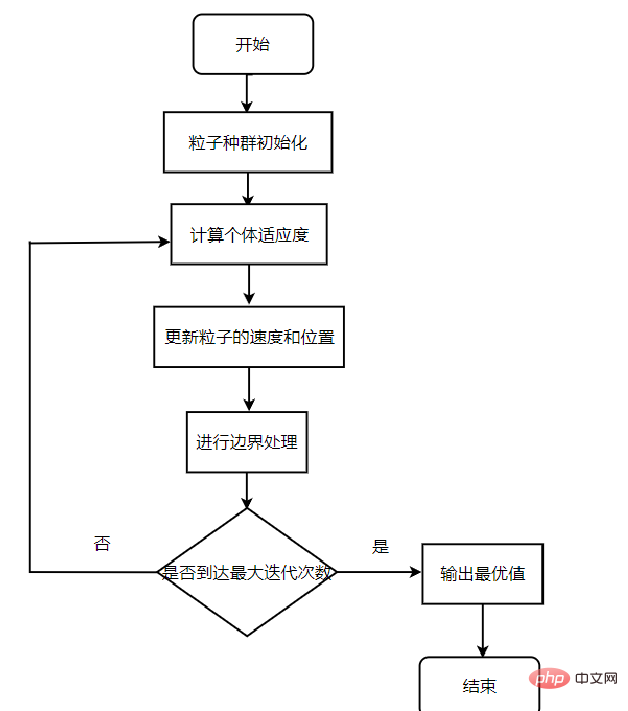
Le processus principal de l'algorithme :
La première étape : initialiser la position et la vitesse aléatoires de l'essaim de particules, et définir Déterminez le nombre d’itérations.
Étape 2 : Calculez la valeur de fitness de chaque particule.
La troisième étape : pour chaque particule, comparez sa valeur de condition physique avec la valeur de forme physique de la meilleure position que j'ai connue. Si elle est meilleure, utilisez-la comme meilleur emplacement individuel actuel.
Étape 4 : Pour chaque particule, comparez sa valeur de condition physique avec la valeur de forme physique de la meilleure position expérimentée dans le monde. Si elle est meilleure, utilisez-la comme meilleur emplacement mondial actuel.
Étape 5 : Optimisez la vitesse et la position des particules en fonction des formules de vitesse et de position pour mettre à jour la position des particules.
Étape 6 : Si la condition de fin n'est pas remplie (généralement le nombre maximum de cycles ou l'exigence d'erreur minimale), revenez à la deuxième étape
 # 🎜🎜#
# 🎜🎜#
import numpy as np
import random
class PSO_model:
def __init__(self,w,c1,c2,r1,r2,N,D,M):
self.w = w # 惯性权值
self.c1=c1
self.c2=c2
self.r1=r1
self.r2=r2
self.N=N # 初始化种群数量个数
self.D=D # 搜索空间维度
self.M=M # 迭代的最大次数
self.x=np.zeros((self.N,self.D)) #粒子的初始位置
self.v=np.zeros((self.N,self.D)) #粒子的初始速度
self.pbest=np.zeros((self.N,self.D)) #个体最优值初始化
self.gbest=np.zeros((1,self.D)) #种群最优值
self.p_fit=np.zeros(self.N)
self.fit=1e8 #初始化全局最优适应度
# 目标函数,也是适应度函数(求最小化问题)
def function(self,x):
A = 10
x1=x[0]
x2=x[1]
Z = 2 * A + x1 ** 2 - A * np.cos(2 * np.pi * x1) + x2 ** 2 - A * np.cos(2 * np.pi * x2)
return Z
# 初始化种群
def init_pop(self):
for i in range(self.N):
for j in range(self.D):
self.x[i][j] = random.random()
self.v[i][j] = random.random()
self.pbest[i] = self.x[i] # 初始化个体的最优值
aim=self.function(self.x[i]) # 计算个体的适应度值
self.p_fit[i]=aim # 初始化个体的最优位置
if aim < self.fit: # 对个体适应度进行比较,计算出最优的种群适应度
self.fit = aim
self.gbest = self.x[i]
# 更新粒子的位置与速度
def update(self):
for t in range(self.M): # 在迭代次数M内进行循环
for i in range(self.N): # 对所有种群进行一次循环
aim=self.function(self.x[i]) # 计算一次目标函数的适应度
if aim<self.p_fit[i]: # 比较适应度大小,将小的负值给个体最优
self.p_fit[i]=aim
self.pbest[i]=self.x[i]
if self.p_fit[i]<self.fit: # 如果是个体最优再将和全体最优进行对比
self.gbest=self.x[i]
self.fit = self.p_fit[i]
for i in range(self.N): # 更新粒子的速度和位置
self.v[i]=self.w*self.v[i]+self.c1*self.r1*(self.pbest[i]-self.x[i])+ self.c2*self.r2*(self.gbest-self.x[i])
self.x[i]=self.x[i]+self.v[i]
print("最优值:",self.fit,"位置为:",self.gbest)
if __name__ == '__main__':
# w,c1,c2,r1,r2,N,D,M参数初始化
w=random.random()
c1=c2=2#一般设置为2
r1=0.7
r2=0.5
N=30
D=2
M=200
pso_object=PSO_model(w,c1,c2,r1,r2,N,D,M)#设置初始权值
pso_object.init_pop()
pso_object.update()Solution au TSP
# 群体的初始化和路径的初始化
self.population = np.array([0] * self.num_pop * self.num).reshape(
self.num_pop, self.num)
self.fitness = [0] * self.num_pop
"""
计算城市的距离,我们用矩阵表示城市间的距离
"""
self.__matrix_distance = self.__matrix_dis()DIFFERENCE
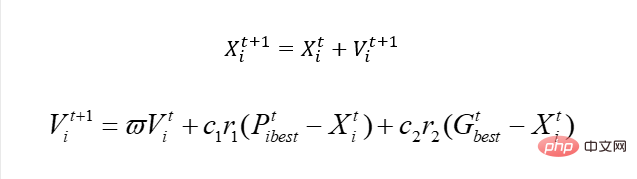 De même, nous pouvons utiliser X pour représenter le numéro de la ville, mais évidemment nous ne pouvons pas utilisez cette solution Effectuez des mises à jour rapides.
De même, nous pouvons utiliser X pour représenter le numéro de la ville, mais évidemment nous ne pouvons pas utilisez cette solution Effectuez des mises à jour rapides.
Donc à ce moment-là, lorsque nous mettons à jour la vitesse, nous devons utiliser une nouvelle solution. Cette solution est donc en fait la mise à jour X utilisant l'algorithme de calcul génétique. Pour le dire franchement, la raison pour laquelle nous avons besoin de vitesse est de mettre à jour X et de faire avancer X dans la bonne direction. Maintenant, il n'est plus possible d'utiliser simplement la mise à jour rapide, nous mettons donc à jour X de toute façon, alors pourquoi ne pas simplement choisir une solution qui peut bien mettre à jour ce X ? Par conséquent, la génétique peut être utilisée directement ici. Notre mise à jour rapide est basée sur Pbest et Gbest, puis « apprise » selon un certain poids, de cette façon, ce V a une « caractéristique » de Pbest et Gbest. Donc, si tel est le cas, alors lorsque j'imite directement le croisement génétique et que je le croise avec Best, ne puis-je pas apprendre certaines « caractéristiques » correspondantes ?
def cross_1(self, path, best_path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
cross = best_path[left:right + 1]
for i in range(right - left + 1):
for k in range(self.num):
if path[k] == cross[i]:
path[k:self.num - 1] = path[k + 1:self.num]
path[-1] = 0
path[self.num - right + left - 1:self.num] = cross
return pathEn même temps, on peut encore introduire des mutations.
def mutation(self,path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
path[r1],path[r2] = path[r2],path[r1]
return pathCode complet
import numpy as np
import matplotlib.pyplot as plt
class HybridPsoTSP(object):
def __init__(self ,data ,num_pop=200):
self.num_pop = num_pop # 群体个数
self.data = data # 城市坐标
self.num =len(data) # 城市个数
# 群体的初始化和路径的初始化
self.population = np.array([0] * self.num_pop * self.num).reshape(
self.num_pop, self.num)
self.fitness = [0] * self.num_pop
"""
计算城市的距离,我们用矩阵表示城市间的距离
"""
self.__matrix_distance = self.__matrix_dis()
def __matrix_dis(self):
"""
计算14个城市的距离,将这些距离用矩阵存起来
:return:
"""
res = np.zeros((self.num, self.num))
for i in range(self.num):
for j in range(i + 1, self.num):
res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
res[j, i] = res[i, j]
return res
def cross_1(self, path, best_path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
cross = best_path[left:right + 1]
for i in range(right - left + 1):
for k in range(self.num):
if path[k] == cross[i]:
path[k:self.num - 1] = path[k + 1:self.num]
path[-1] = 0
path[self.num - right + left - 1:self.num] = cross
return path
def mutation(self,path):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
path[r1],path[r2] = path[r2],path[r1]
return path
def comp_fit(self, one_path):
"""
计算,咱们这个路径的长度,例如A-B-C-D
:param one_path:
:return:
"""
res = 0
for i in range(self.num - 1):
res += self.__matrix_distance[one_path[i], one_path[i + 1]]
res += self.__matrix_distance[one_path[-1], one_path[0]]
return res
def out_path(self, one_path):
"""
输出我们的路径顺序
:param one_path:
:return:
"""
res = str(one_path[0] + 1) + '-->'
for i in range(1, self.num):
res += str(one_path[i] + 1) + '-->'
res += str(one_path[0] + 1) + '\n'
print(res)
def init_population(self):
"""
初始化种群
:return:
"""
rand_ch = np.array(range(self.num))
for i in range(self.num_pop):
np.random.shuffle(rand_ch)
self.population[i, :] = rand_ch
self.fitness[i] = self.comp_fit(rand_ch)
def main(data, max_n=200, num_pop=200):
Path_short = HybridPsoTSP(data, num_pop=num_pop) # 混合粒子群算法类
Path_short.init_population() # 初始化种群
# 初始化路径绘图
fig, ax = plt.subplots()
x = data[:, 0]
y = data[:, 1]
ax.scatter(x, y, linewidths=0.1)
for i, txt in enumerate(range(1, len(data) + 1)):
ax.annotate(txt, (x[i], y[i]))
res0 = Path_short.population[0]
x0 = x[res0]
y0 = y[res0]
for i in range(len(data) - 1):
plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.show()
print('初始染色体的路程: ' + str(Path_short.fitness[0]))
# 存储个体极值的路径和距离
best_P_population = Path_short.population.copy()
best_P_fit = Path_short.fitness.copy()
min_index = np.argmin(Path_short.fitness)
# 存储当前种群极值的路径和距离
best_G_population = Path_short.population[min_index, :]
best_G_fit = Path_short.fitness[min_index]
# 存储每一步迭代后的最优路径和距离
best_population = [best_G_population]
best_fit = [best_G_fit]
# 复制当前群体进行交叉变异
x_new = Path_short.population.copy()
for i in range(max_n):
# 更新当前的个体极值
for j in range(num_pop):
if Path_short.fitness[j] < best_P_fit[j]:
best_P_fit[j] = Path_short.fitness[j]
best_P_population[j, :] = Path_short.population[j, :]
# 更新当前种群的群体极值
min_index = np.argmin(Path_short.fitness)
best_G_population = Path_short.population[min_index, :]
best_G_fit = Path_short.fitness[min_index]
# 更新每一步迭代后的全局最优路径和解
if best_G_fit < best_fit[-1]:
best_fit.append(best_G_fit)
best_population.append(best_G_population)
else:
best_fit.append(best_fit[-1])
best_population.append(best_population[-1])
# 将每个个体与个体极值和当前的群体极值进行交叉
for j in range(num_pop):
# 与个体极值交叉
x_new[j, :] = Path_short.cross_1(x_new[j, :], best_P_population[j, :])
fit = Path_short.comp_fit(x_new[j, :])
# 判断是否保留
if fit < Path_short.fitness[j]:
Path_short.population[j, :] = x_new[j, :]
Path_short.fitness[j] = fit
# 与当前极值交叉
x_new[j, :] = Path_short.cross_1(x_new[j, :], best_G_population)
fit = Path_short.comp_fit(x_new[j, :])
if fit < Path_short.fitness[j]:
Path_short.population[j, :] = x_new[j, :]
Path_short.fitness[j] = fit
# 变异
x_new[j, :] = Path_short.mutation(x_new[j, :])
fit = Path_short.comp_fit(x_new[j, :])
if fit <= Path_short.fitness[j]:
Path_short.population[j] = x_new[j, :]
Path_short.fitness[j] = fit
if (i + 1) % 20 == 0:
print('第' + str(i + 1) + '步后的最短的路程: ' + str(Path_short.fitness[min_index]))
print('第' + str(i + 1) + '步后的最优路径:')
Path_short.out_path(Path_short.population[min_index, :]) # 显示每一步的最优路径
Path_short.best_population = best_population
Path_short.best_fit = best_fit
return Path_short # 返回结果类
if __name__ == '__main__':
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
main(data)初始染色体的路程: 71.30211569672313
第20步后的最短的路程: 29.340520066994223
第20步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第40步后的最短的路程: 29.340520066994223
第40步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第60步后的最短的路程: 29.340520066994223
第60步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第80步后的最短的路程: 29.340520066994223
第80步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第100步后的最短的路程: 29.340520066994223
第100步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第120步后的最短的路程: 29.340520066994223
第120步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第140步后的最短的路程: 29.340520066994223
第140步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第160步后的最短的路程: 29.340520066994223
第160步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第180步后的最短的路程: 29.340520066994223
第180步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
第200步后的最短的路程: 29.340520066994223
第200步后的最优路径:
9-->10-->1-->2-->14-->3-->4-->5-->6-->12-->7-->13-->8-->11-->9
可以看到收敛速度还是很快的。
ok,到目前为止的话,我们介绍了两个算法去解决TSP或者是优化问题。我们来分析一下,这些算法有什么特点,为啥可以达到我们需要的优化效果。其实不管是遗传还是PSO,你其实都可以发现,有一个东西,我们可以暂且叫它环境压力。我们通过物竞天择,或者鸟类迁移,进行模拟寻优。而之所以需要这样做,是因为我们指定了一个规则,在我们的规则之下。我们让模拟的种群有一种压力去靠拢,其中物竞天择和鸟类迁移只是我们的一种手段,去应对这样的“压力”。所以的对于这种算法而言,最核心的点就两个:
我们需要做优化问题,所以我们必须要能够让我们的解往那个方向走,需要一个驱动,需要一个压力。因此我们需要设计这样的一个环境,在遗传算法,粒子群算法是通过种群当中的生存,来进行设计的它的压力是我们的目标函数。由种群和目标函数(目标指标)构成了一个环境和压力。
之后的话,我们设计好了一个环境和压力,那么未来应对这种压力,我们需要去设计一种策略,来应付这种压力。遗传算法是通过PUA自己,也就是种群的优胜略汰。PSO是通过学习,学习种群的优秀粒子和过去自己家的优秀“祖先”来应对这种压力的。
所以的话,我们是否可以使用别的方案来实现这种优化效果。,在强化学习的算法框架里面的话,我们明确的知道了为什么他们可以实现优化,是环境压力+压力策略。恰好咱们强化学习是有环境的,适应函数和环境恰好可以组成环境+压力。本身的算法收敛过程就是我们的压力策略。所以我们完全是可以直接使用强化学习进行这个处理的。那么在这里咱们就来使用强化学习在下一篇文章当中。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!