Problème TSP
Alors avant de commencer, décrivons ce problème TSP en détail. Les amis qui ont fait de la modélisation numérique ou qui ont été exposés à l'optimisation intelligente ou à l'apprentissage automatique devraient tous le savoir. Bien sûr, dans l'intérêt du public universel de cet article, nous ferons de notre mieux pour le rendre aussi parfait et clair que possible. ici, afin que nous puissions réellement résoudre le problème.
Donc le problème est en fait simple, il ressemble à ceci :
Dans notre plan à N dimensions, ce dont nous parlons aujourd'hui est de ce plan à deux dimensions. Il y a de nombreuses villes sur ce plan, et parmi les. villes Les villes sont reliées entre elles. Nous devons maintenant trouver le chemin le plus court pour visiter toutes les villes. Par exemple, nous avons les villes A, B, C, D, E. Maintenant que nous connaissons les coordonnées entre les villes, ce qui équivaut à connaître la distance entre les villes, nous pouvons maintenant trouver une séquence qui peut tracer le chemin le plus court vers toutes les villes A, B, C, D et E. Par exemple, après calcul, cela peut être B-->A-->C-->E-->D. En d’autres termes, trouvez cet ordre.
Énumération
Si nous voulons d'abord résoudre ce problème, il existe en fait de nombreuses solutions. Pour parler franchement, il nous suffit de trouver un ordre qui puisse minimiser la somme des chemins. Ensuite, la chose la plus simple à laquelle penser est l'énumération. Par exemple, laissez A aller d'abord, puis voyez si la distance la plus proche de A est B, puis allez à B, puis partez de B. Bien sûr, il s’agit d’une stratégie locale gourmande, et il est facile d’atteindre l’optimum local. On peut alors considérer DP à ce moment-là, c’est-à-dire que l’on part toujours de A, puis s’assurer que 2 villes sont. la plus courte, 3 villes sont les plus courtes et 4 et 5 sont les plus courtes. Enfin, supposons la même chose de B. Ou énumérez directement toutes les situations et calculez la distance. Quoi qu’il en soit, à mesure que le nombre de villes augmente, leur complexité va augmenter. Nous devons donc trouver des moyens de faire en sorte que l’informatique utilise notre expertise humaine. J'appelle cela "la cécité".
Algorithme Intelligent
Parlons maintenant de cet algorithme intelligent et pourquoi nous l'utilisons. Nous venons de dire que la solution précédente nécessiterait beaucoup de calculs pour une grande quantité de données, et qu'elle n'est pas forcément facile à écrire. Donc à ce stade, tout d’abord, pour le seul problème TSP, ce que nous voulons, c’est une séquence, une séquence qui ne se répétera pas. Alors à l’heure actuelle, existe-t-il une solution plus simple ? Et lorsque les données sont suffisamment volumineuses, nous n’avons pas nécessairement besoin d’une solution complètement précise et complètement minimale, du moment qu’elle est proche. Donc à l'heure actuelle, si nous utilisons des algorithmes traditionnels, un est un. Le calcul ne sera effectué que selon nos règles, et nous ne savons vraiment pas quelle est la réponse standard. Il est également difficile de fixer un seuil pour arrêter le calcul. algorithmes traditionnels. Mais pour nous, il y a quelque chose qui s'appelle « chance ». Certaines personnes ont tellement de chance qu'elles peuvent être confuses quant à la réponse dès qu'elles entrent dans leur âme. Notre algorithme intelligent est donc en fait un peu similaire à "Monkey". Mais les gens font attention aux compétences. Par exemple, l'expérience nous dit que trois longs et un court sont les plus courts. Vous pouvez utiliser cette technique pour deviner la réponse. Ou lorsque vous recherchez un petit ami aussi beau qu'un blogueur. vous n'avez besoin que d'un morceau de la série 40 (30, c'est également bien). La carte graphique peut être facilement retirée. Meng nécessite des compétences, nous appelons cette stratégie.
Stratégie
Donc cette technique dont on vient de parler, cette astuce. Dans les algorithmes intelligents, ce masque est l’une de nos stratégies. Comment pouvons-nous nous en débarrasser pour que notre solution soit plus raisonnable ? Puis à ce moment-là, une centaine de fleurs fleuriront. Je ne chanterai pas de sutras ici. Prenons comme exemples les deux algorithmes les plus classiques, l'un est l'algorithme génétique et l'autre est l'algorithme d'essaim de particules (PSO). À titre d'exemple, ils utilisent une stratégie de décryptage, telle qu'un algorithme génétique. En simulant la sélection naturelle, ils génèrent aléatoirement un tas de solutions et un tas de séquences au début, puis utilisent notre stratégie de sélection naturelle pour générer des solutions. solutions, puis utilisez ces solutions pour trouver de nouvelles et meilleures solutions. Après de nombreux allers-retours, j'ai finalement trouvé une bonne solution. L'essaim de particules est similaire. Nous expliquerons ces parties en détail lorsque nous les utiliserons.
Algorithme
Maintenant que nous connaissons déjà cette stratégie, qu'est-ce que l'algorithme ? Il s'agit en fait des étapes pour mettre en œuvre ces stratégies, qui sont notre code, notre boucle et la structure des données. Nous devons comprendre ce que nous venons de mentionner, comme la sélection naturelle, comme notre TSP, comment générer aléatoirement un tas de solutions.
Échantillon de données
ok, nous avons fini de parler de quelques concepts de base ici, alors à ce moment-là, regardons comment nous exprimons ce problème TSP. C'est en fait très simple. De notre côté, c'est simple. une donnée de test. Supposons qu'il y ait 14 villes ici. Ensuite, nos données pour ces villes sont les suivantes :
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))Copier après la connexion
Nous utiliserons cet ensemble de données pour tester plus tard, et il y a maintenant 14 villes dessus.
Ensuite, commençons notre solution
Algorithme génétique
ok, puis parlons de ce qu'est notre algorithme génétique, puis nous l'utiliserons pour résoudre ce problème de TSP.
Alors maintenant, voyons comment notre algorithme génétique est trompé.
算法流程
遗传算法其实是在用计算机模拟我们的物种进化。其实更加通俗的说法是筛选，这个就和我们袁老爷爷种植水稻一样。有些个体发育良好，有些个体发育不好，那么我就先筛选出发育好的，然后让他们去繁衍后代，然后再筛选，最后得到高产水稻。其实也和我们社会一样，不努力就木有女朋友就不能保留自己的基因，然后剩下的人就是那些优秀的人和富二代的基因，这就是现实呀。所以得好好学习，天天向上！
那么回到主题，我们的遗传算法就是在模拟这一个过程，模拟一个物竞天择的过程。
所以在我们的算法里面也是分为几大块
繁殖
首先我们的种群需要先繁殖。这样才能不断产生优良基于，那么对应我们的算法，假设我们需要求取
Y = np.sin(10 * x) * x + np.cos(2 * x) * x
的最大值（在一个范围内）那么我们的个体就是一组（X1）的解。好的个体就会被保留，不好的就会被pass，选择标准就是我们的函数 Y 。那么问题来了如何模拟这个过程？我们都知道在繁殖后代的时候我们是通过DNA来保留我们的基因信息，在这个过程当中，父母的DNA交互，并且在这个过程当中会产生变异，这样一来，父母双方的优秀基于会被保存，并且产生的变异有可能诞生更加优秀的后代。
所以接下来我们需要模拟我们的ＤＮＡ，进行交叉和变异。
交叉
这个交叉过程和我们的生物其实很像，当然我们在我们的计算机里面对于数字我们可以将其转化为二进制，当做我们的DNA
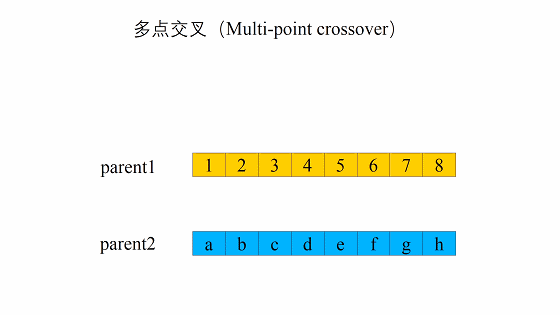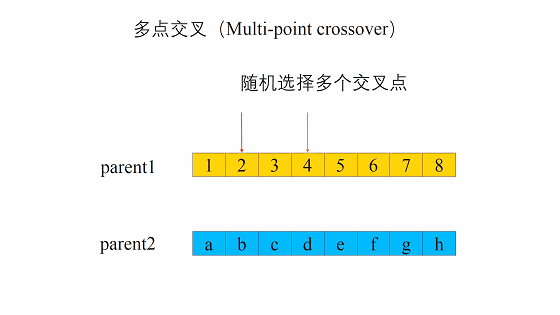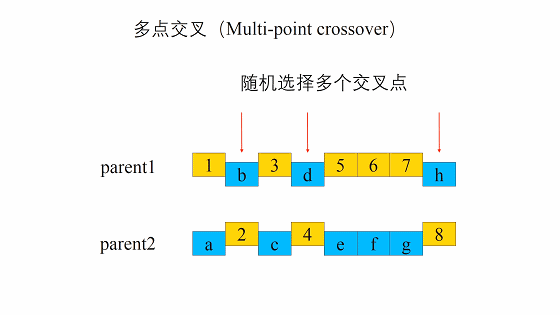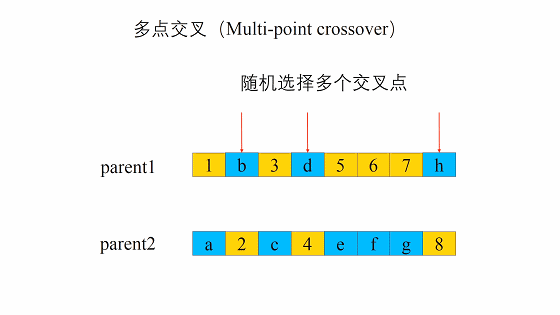
交叉的方式有很多，我们这边选择这一个，进行交叉。
变异
那这个在我们这里就更加简单了
我们只需要在交叉之后，再随机选择几个位置进行改变值就可以了。当然变异的概率是很小的，并且是随机的，这一点要注意。并且由于变异是随机的，所以不排除生成比原来还更加糟糕的个体。
选择
最后我们按照一定的规则去筛选这个些个体就可以了，然后淘汰原来的个体。那么在我们的计算机里面是使用了两个东西，首先我们要把原来二进制的玩意，给转化为我们原来的十进制然后带入我们的函数运算，然后保存起来，之后再每一轮统一筛选一下就好了。
逆转
这个咋说呢，说好听点叫逆转，难听点就算，对于一些新的生成的不好的解，我们是要舍弃的。
代码
那么这部分用代码描述的话就是这样的：
import numpy as np
import matplotlib.pyplot as plt
Population_Size = 100
Iteration_Number = 200
Cross_Rate = 0.8
Mutation_Rate = 0.003
Dna_Size = 10
X_Range=[0,5]
def F(x):
'''
目标函数，需要被优化的函数
:param x:
:return:
'''
return np.sin(10 * x) * x + np.cos(2 * x) * x
def CrossOver(Parent,PopSpace):
'''
交叉DNA，我们直接在种群里面选择一个交配
然后就生出孩子了
:param parent:
:param PopSpace:
:return:
'''
if(np.random.rand()) < Cross_Rate:
cross_place = np.random.randint(0, 2, size=Dna_Size).astype(np.bool)
cross_one = np.random.randint(0, Population_Size, size=1) #选择一位男/女士交配
Parent[cross_place] = PopSpace[cross_one,cross_place]
return Parent
def Mutate(Child):
'''
变异
:param Child:
:return:
'''
for point in range(Dna_Size):
if np.random.rand() < Mutation_Rate:
Child[point] = 1 if Child[point] == 0 else 0
return Child
def TranslateDNA(PopSpace):
'''
把二进制转化为十进制方便计算
:param PopSpace:
:return:
'''
return PopSpace.dot(2 ** np.arange(Dna_Size)[::-1]) / float(2 ** Dna_Size - 1) * X_Range[1]
def Fitness(pred):
'''
这个其实是对我们得到的F(x)进行换算，其实就是选择的时候
的概率，我们需要处理负数，因为概率不能为负数呀
pred 这是一个二维矩阵
:param pred:
:return:
'''
return pred + 1e-3 - np.min(pred)
def Select(PopSpace,Fitness):
'''
选择
:param PopSpace:
:param Fitness:
:return:
'''
'''
这里注意的是，我们先按照权重去选择我们的优良个体，所以我们这里选择的时候允许重复的元素出现
之后我们就可以去掉这些重复的元素，这样才能实现保留良种去除劣种。100--》70（假设有30个重复）
如果不允许重复的话，那你相当于没有筛选
'''
Better_Ones = np.random.choice(np.arange(Population_Size), size=Population_Size, replace=True,
p=Fitness / Fitness.sum())
# np.unique(Better_Ones) #这个是我后面加的
return PopSpace[Better_Ones]
if __name__ == '__main__':
PopSpace = np.random.randint(2, size=(Population_Size, Dna_Size)) # initialize the PopSpace DNA
plt.ion()
x = np.linspace(X_Range, 200)
# plt.plot(x, F(x))
plt.xticks([0,10])
plt.yticks([0,10])
for _ in range(Iteration_Number):
F_values = F(TranslateDNA(PopSpace))
# something about plotting
if 'sca' in globals():
sca.remove()
sca = plt.scatter(TranslateDNA(PopSpace), F_values, s=200, lw=0, c='red', alpha=0.5)
plt.pause(0.05)
# GA part (evolution)
fitness = Fitness(F_values)
print("Most fitted DNA: ", PopSpace[np.argmax(fitness)])
PopSpace = Select(PopSpace, fitness)
PopSpace_copy = PopSpace.copy()
for parent in PopSpace:
child = CrossOver(parent, PopSpace_copy)
child = Mutate(child)
parent[:] = child
plt.ioff()
plt.show()Copier après la connexion
这个代码是以前写的，逆转没有写上（下面的有）
TSP遗传算法
ok,刚刚的例子是拿的解方程，也就是说是一个连续问题吧，当然那个连续处理的话并不是很好，只是一个演示。那么我们这个的话其实类似的。首先我们的ＤＮＡ，是城市的路径，也就是A-B-C-D等等，当然我们用下标表示城市。
种群表示
首先我们确定了使用城市的序号作为我们的个体DNA，例如咱们种群大小为100，有ＡＢＣＤ四个城市，那么他就是这样的，我们先随机生成种群，长这个样：
1 2 3 4
2 3 4 5
3 2 1 4
...
那个1,2,3,4是ABCD的序号。
交叉与变异
这里面的话，值得一提的就是，由于暂定城市需要是不能重复的，且必须是完整的，所以如果像刚刚那样进行交叉或者变异的话，那么实际上会出点问题，我们不允许出现重复，且必须完整，对于我们的DNA，也就是咱们瞎蒙的个体。
代码
由于咱们每一步在代码里面都有注释，所以的话咱们在这里就不再进行复述了。
from math import floor
import numpy as np
import matplotlib.pyplot as plt
class Gena_TSP(object):
"""
使用遗传算法解决TSP问题
"""
def __init__(self, data, maxgen=200,
size_pop=200, cross_prob=0.9,
pmuta_prob=0.01, select_prob=0.8
):
self.maxgen = maxgen # 最大迭代次数
self.size_pop = size_pop # 群体个数，（一次性瞎蒙多少个解）
self.cross_prob = cross_prob # 交叉概率
self.pmuta_prob = pmuta_prob # 变异概率
self.select_prob = select_prob # 选择概率
self.data = data # 城市的坐标数据
self.num = len(data) # 有多少个城市，对应多少个坐标，对应染色体的长度（我们的解叫做染色体）
"""
计算城市的距离，我们用矩阵表示城市间的距离
"""
self.__matrix_distance = self.__matrix_dis()
self.select_num = int(self.size_pop * self.select_prob)
# 通过选择概率确定子代的选择个数
"""
初始化子代和父代种群，两者相互交替
"""
self.parent = np.array([0] * self.size_pop * self.num).reshape(self.size_pop, self.num)
self.child = np.array([0] * self.select_num * self.num).reshape(self.select_num, self.num)
"""
负责计算每一个个体的（瞎蒙的解）最后需要多少距离
"""
self.fitness = np.zeros(self.size_pop)
self.best_fit = []
self.best_path = []
# 保存每一步的群体的最优路径和距离
def __matrix_dis(self):
"""
计算14个城市的距离，将这些距离用矩阵存起来
:return:
"""
res = np.zeros((self.num, self.num))
for i in range(self.num):
for j in range(i + 1, self.num):
res[i, j] = np.linalg.norm(self.data[i, :] - self.data[j, :])
res[j, i] = res[i, j]
return res
def rand_parent(self):
"""
初始化种群
:return:
"""
rand_ch = np.array(range(self.num))
for i in range(self.size_pop):
np.random.shuffle(rand_ch)
self.parent[i, :] = rand_ch
self.fitness[i] = self.comp_fit(rand_ch)
def comp_fit(self, one_path):
"""
计算，咱们这个路径的长度，例如A-B-C-D
:param one_path:
:return:
"""
res = 0
for i in range(self.num - 1):
res += self.__matrix_distance[one_path[i], one_path[i + 1]]
res += self.__matrix_distance[one_path[-1], one_path[0]]
return res
def out_path(self, one_path):
"""
输出我们的路径顺序
:param one_path:
:return:
"""
res = str(one_path[0] + 1) + '-->'
for i in range(1, self.num):
res += str(one_path[i] + 1) + '-->'
res += str(one_path[0] + 1) + '\n'
print(res)
def Select(self):
"""
通过我们的这个计算的距离来计算出概率，也就是当前这些个体DNA也就瞎蒙的解
之后我们在通过概率去选择个体，放到child里面
:return:
"""
fit = 1. / (self.fitness) # 适应度函数
cumsum_fit = np.cumsum(fit)
pick = cumsum_fit[-1] / self.select_num * (np.random.rand() + np.array(range(self.select_num)))
i, j = 0, 0
index = []
while i < self.size_pop and j < self.select_num:
if cumsum_fit[i] >= pick[j]:
index.append(i)
j += 1
else:
i += 1
self.child = self.parent[index, :]
def Cross(self):
"""
模仿DNA交叉嘛，就是交换两个瞎蒙的解的部分的解例如
A-B-C-D
C-D-A-B
我们选几个交叉例如这样
A-D-C-B
1,3号交换了位置，当然这里注意可不能重复啊
:return:
"""
if self.select_num % 2 == 0:
num = range(0, self.select_num, 2)
else:
num = range(0, self.select_num - 1, 2)
for i in num:
if self.cross_prob >= np.random.rand():
self.child[i, :], self.child[i + 1, :] = self.intercross(self.child[i, :],
self.child[i + 1, :])
def intercross(self, ind_a, ind_b):
"""
这个是我们两两交叉的具体实现
:param ind_a:
:param ind_b:
:return:
"""
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
ind_a1 = ind_a.copy()
ind_b1 = ind_b.copy()
for i in range(left, right + 1):
ind_a2 = ind_a.copy()
ind_b2 = ind_b.copy()
ind_a[i] = ind_b1[i]
ind_b[i] = ind_a1[i]
x = np.argwhere(ind_a == ind_a[i])
y = np.argwhere(ind_b == ind_b[i])
if len(x) == 2:
ind_a[x[x != i]] = ind_a2[i]
if len(y) == 2:
ind_b[y[y != i]] = ind_b2[i]
return ind_a, ind_b
def Mutation(self):
"""
之后是变异模块，这个就是按照某个概率，去替换瞎蒙的解里面的其中几个元素。
:return:
"""
for i in range(self.select_num):
if np.random.rand() <= self.cross_prob:
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
self.child[i, [r1, r2]] = self.child[i, [r2, r1]]
def Reverse(self):
"""
近化逆转，就是说下一次瞎蒙的解如果没有更好的话就不进入下一代，同时也是随机选择一个部分的
我们不是一次性全部替换
:return:
"""
for i in range(self.select_num):
r1 = np.random.randint(self.num)
r2 = np.random.randint(self.num)
while r2 == r1:
r2 = np.random.randint(self.num)
left, right = min(r1, r2), max(r1, r2)
sel = self.child[i, :].copy()
sel[left:right + 1] = self.child[i, left:right + 1][::-1]
if self.comp_fit(sel) < self.comp_fit(self.child[i, :]):
self.child[i, :] = sel
def Born(self):
"""
替换，子代变成新的父代
:return:
"""
index = np.argsort(self.fitness)[::-1]
self.parent[index[:self.select_num], :] = self.child
def main(data):
Path_short = Gena_TSP(data) # 根据位置坐标，生成一个遗传算法类
Path_short.rand_parent() # 初始化父类
## 绘制初始化的路径图
fig, ax = plt.subplots()
x = data[:, 0]
y = data[:, 1]
ax.scatter(x, y, linewidths=0.1)
for i, txt in enumerate(range(1, len(data) + 1)):
ax.annotate(txt, (x[i], y[i]))
res0 = Path_short.parent[0]
x0 = x[res0]
y0 = y[res0]
for i in range(len(data) - 1):
plt.quiver(x0[i], y0[i], x0[i + 1] - x0[i], y0[i + 1] - y0[i], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.quiver(x0[-1], y0[-1], x0[0] - x0[-1], y0[0] - y0[-1], color='r', width=0.005, angles='xy', scale=1,
scale_units='xy')
plt.show()
print('初始染色体的路程: ' + str(Path_short.fitness[0]))
# 循环迭代遗传过程
for i in range(Path_short.maxgen):
Path_short.Select() # 选择子代
Path_short.Cross() # 交叉
Path_short.Mutation() # 变异
Path_short.Reverse() # 进化逆转
Path_short.Born() # 子代插入
# 重新计算新群体的距离值
for j in range(Path_short.size_pop):
Path_short.fitness[j] = Path_short.comp_fit(Path_short.parent[j, :])
index = Path_short.fitness.argmin()
if (i + 1) % 50 == 0:
print('第' + str(i + 1) + '步后的最短的路程: ' + str(Path_short.fitness[index]))
print('第' + str(i + 1) + '步后的最优路径:')
Path_short.out_path(Path_short.parent[index, :]) # 显示每一步的最优路径
# 存储每一步的最优路径及距离
Path_short.best_fit.append(Path_short.fitness[index])
Path_short.best_path.append(Path_short.parent[index, :])
return Path_short # 返回遗传算法结果类
if __name__ == '__main__':
data = np.array([16.47, 96.10, 16.47, 94.44, 20.09, 92.54,
22.39, 93.37, 25.23, 97.24, 22.00, 96.05, 20.47, 97.02,
17.20, 96.29, 16.30, 97.38, 14.05, 98.12, 16.53, 97.38,
21.52, 95.59, 19.41, 97.13, 20.09, 92.55]).reshape((14, 2))
main(data)Copier après la connexion
运行结果
ok,我们来看看运行的结果：
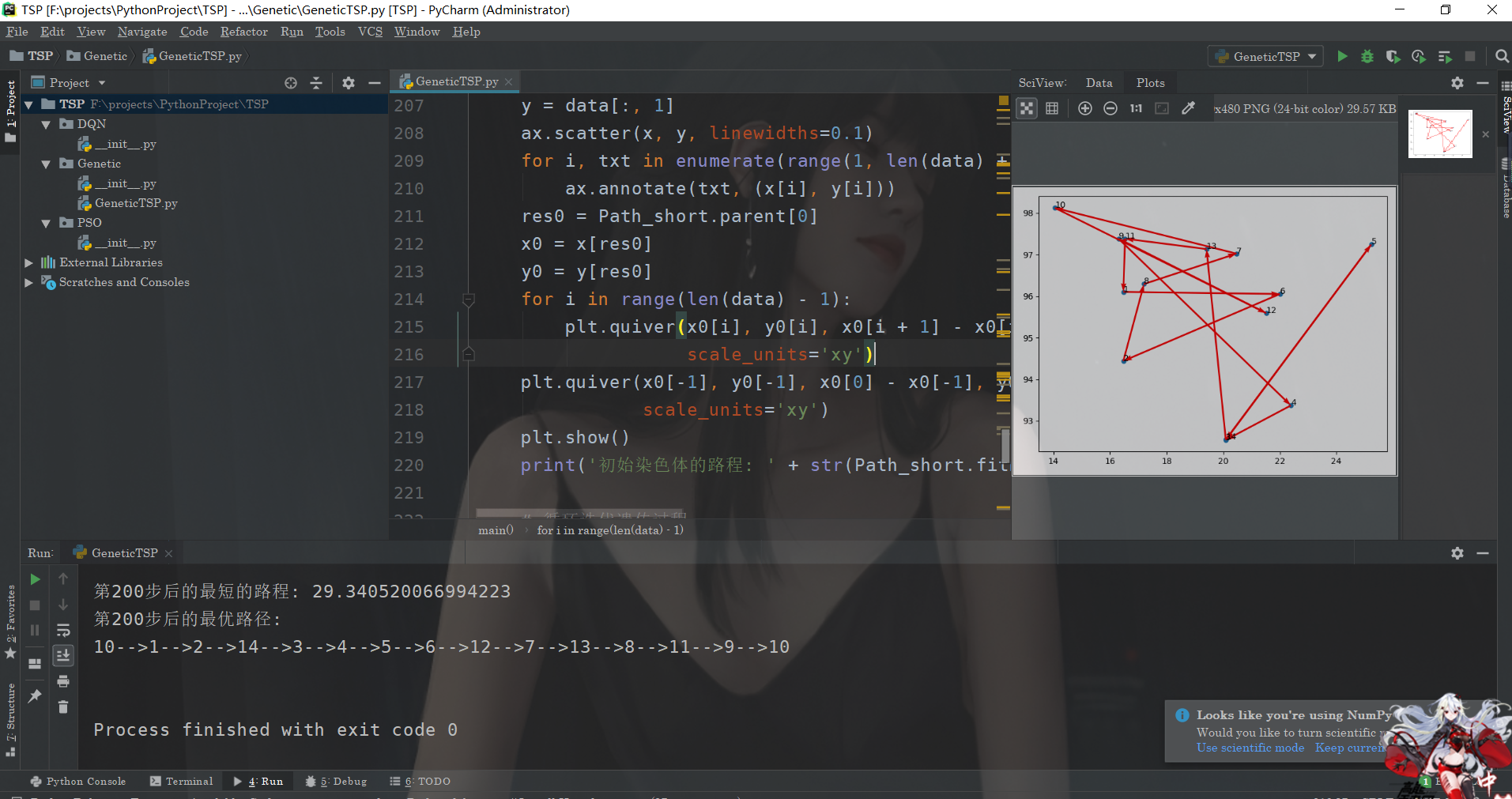
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
