
Chicken Swarm Optimization, en abrégé CSO (Chicken Swarm Optimization), bien qu'il ait une formation en bionique, il s'agit essentiellement d'une variante de l'algorithme d'essaim de particules.
En termes simples, un essaim de particules est un groupe de particules. Chaque particule a sa propre position et sa propre vitesse, et chaque particule doit être attirée par la meilleure particule. En plus de ces deux règles, les particules sont complètement. égaux les uns aux autres, sauf pour la position et la vitesse.
Bien sûr, l'algorithme d'essaim de particules lui-même a également une base bionique. On dit que l'inspiration est venue d'un troupeau d'oiseaux en quête de nourriture. Ce n'est bien sûr pas important. de particules égales se transformant en un groupe d'oiseaux égaux.
L'algorithme du troupeau de poulets ajoute des caractéristiques d'identité différentes à ces particules, ou à ces oiseaux, afin qu'elles ne soient plus équivalentes les unes aux autres.
Il existe au moins trois classes dans le troupeau de poules, à savoir les coqs, les poules et les poussins. Chaque poule a sa propre position et sa propre vitesse. Mais la différence est que les
les coqs sont les plus arrogants, en principe, ils peuvent se promener avec désinvolture, mais parfois lorsqu'ils remarquent d'autres coqs, ils auront l'idée de. saisir de la nourriture, ce qui équivaut à sélectionner au hasard un autre coq et à affecter sa position.
Les poules sont les plus lésées. D'une part, elles doivent accepter le leadership du coq, et d'autre part, elles doivent rivaliser avec les autres. les poules pour se nourrir
import numpy as np
from random import gauss, random
randint = np.random.randint
uniRand = np.random.uniform
class Chicken:
def __init__(self, N, xRange, order=0, kind=0):
# 生成(N)维参数
self.x = uniRand(*xRange, (N,))
self.best = np.inf
self.xBest = np.zeros((N,))
self.kind = kind # 鸡的类别
self.order = order # 鸡的编号
# 设置自己的首领公鸡
def setCock(self, i):
self.cock = i
# 设置自己的监护母鸡
def setHen(self, i):
self.hen = irandint = np.random.randint
class Swarm:
# cNum 鸡数,是三个元素的列表,分别是公鸡、母鸡和小鸡数
# N参数维度
def __init__(self, cNum, N, xRange):
self.initCs(cNum, N, xRange)
self.bestCS = deepcopy(self.cs) #最佳鸡群
self.best = np.inf #全局最优值
self.xBest = np.zeros((N,)) #全局最优参数
self.N = N
def initCs(self, cNum, N, xRange, vRange):
self.cs = []
self.cNum = cNum
self.cocks = np.arange(cNum[0]) # 公鸡编号
self.hens = np.arange(cNum[0], cNum[0]+cNum[1]) #母鸡编号
self.chicks = np.arange(cNum[0]+cNum[1], np.sum(cNum)) #小鸡编号
kinds = np.repeat([0,1,2], cNum)
for i in range(sum(cNum)):
self.cs.append(Chicken(N,xRange, vRange, i, kinds[i]))
if kinds[i] > 0:
cock = randint(0, cNum[0])
self.cs[i].setCock(cock)
if kinds[i] > 1:
hen = randint(cNum[0], cNum[0]+cNum[1])
self.cs[i].setHen(hen)cock
Rappelez-vous que le numéro du coq actuel est i, et le numéro du coq sélectionné au hasard est j, j≠i , puis le ième La méthode de mise à jour de la position du coq est xi(t+1)=xi(t)⋅( 1+r)# 🎜🎜#où, r est un nombre aléatoire généré par une distribution normale, qui peut être exprimé par 1∼N(0,σ
2), où &sigma ;2 est
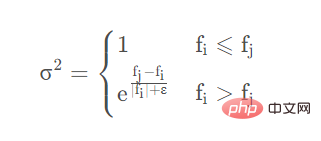 où f est généralement appelé le facteur de condition physique, qui est équivalent à la valeur obtenue en bourrant un certain poulet dans la fonction à résoudre. Par exemple, si vous souhaitez rechercher la valeur minimale de y=
où f est généralement appelé le facteur de condition physique, qui est équivalent à la valeur obtenue en bourrant un certain poulet dans la fonction à résoudre. Par exemple, si vous souhaitez rechercher la valeur minimale de y=
, si la position actuelle du poulet est 1,5, alors f=1,52=2,25 . ε est une petite quantité qui évite les erreurs de division par zéro. Mais il faut noter que tous les x ci-dessus ne représentent pas un scalaire, mais un tableau.
Son implémentation Python est
# 写在Swarm类中
def cockStep(self):
for i in self.cocks:
# 第j只公鸡
j = np.random.randint(self.cNum[0])
if j==i:
j = (j+1) % self.cNum[0]
# 第i只公鸡
ci = self.cs[i]
# 第j只公鸡
cj = self.cs[self.cocks[j]]
sigma = 1 if cj.best > ci.best else np.exp(
(cj.best-ci.best)/(np.abs(ci.best)+1e-15))
ci.x *= 1 + gauss(0, sigma)Supposons que le numéro de poule actuel soit i, et cette poule Poulets non seulement il faut suivre le coq leader, mais aussi rivaliser avec d'autres poules pour se nourrir.
x
i(t+1)=xi(t)+k1r#🎜🎜 #1(xc−xi)+k2r2(x# 🎜🎜#j−xi)Parmi eux, xc est son chef coq, pour une autre poule ou coq. k
1,k2 est le coefficient, et sa logique de mise à jour est la même que celle du coq lorsque fi est plus grand. , cela signifie Code implémenté pour #Le dernier est la logique de mise à jour du poussin. est
xi (t+1)=x
(t+1)=x
(t)+r(x
h(t )&moins;xi(t))
où, x#🎜 🎜#h
est la poule gardienne, r est un nombre aléatoire, et l'algorithme est mis en œuvre commedef henStep(self):
nGuarder = self.cNum[0] + self.cNum[1] - 2
for i in self.hens:
guarders = list(self.cocks) + list(self.hens)
c = self.cs[i].cock #首领公鸡
guarders.remove(i)
guarders.remove(c)
# 随机生成另一只监护鸡
j = guarders[np.random.randint(nGuarder)]
ci = self.cs[i]
cj = self.cs[j]
cc = self.cs[c]
k1, k2 = random(), random()
if cc.best > ci.best:
k1 *= np.exp((ci.best-cc.best)/(np.abs(ci.best)+1e-15))
if cj.best < ci.best:
k2 *= np.exp(cj.best-ci.best)
ci.x += k1*(cc.x-ci.x)+k2*(cj.x-ci.x)def chickStep(self):
for i in self.chicks:
ci = self.cs[i]
ci.x += 2*random()*(self.cs[ci.hen].x-ci.x)À ce stade, le cadre de l'algorithme de cluster a été construit avec succès, puis la partie la plus critique, l'optimisation, est implémentée.
其基本逻辑是,输入一个待优化func,通过将每只鸡的位置x带入到这个函数中,得到一个判定值,最后通过这个判定值,来不断更新鸡群。
除了这个函数之外,还需要输入一些其他参数,比如整个鸡群算法的迭代次数,以及鸡群更新的频次等等
# func为待优化函数
# N为迭代次数
# T为鸡群更新周期
def optimize(self, func, N, T, msgT):
for n in range(N):
# 计算优化参数
for c in self.cs:
c.best = func(c.x)
# 分别更新公鸡、母鸡和小鸡
self.cockStep()
self.henStep()
self.chickStep()
if (n+1)%T == 0:
self.update() #每T次更新一次种群
self.printBest(n)
self.printBest(n)其中,printBest可以将当前最佳结果打印出来,其形式为
def printBest(self,n):
fitness = [c.best for c in self.cs]
best = np.min(fitness)
ind = np.where(fitness==best)[0]
msg = f"已经迭代{n}次,最佳优化结果为{np.min(fitness)},参数为:\n"
msg += ", ".join([f"{x:.6f}" for x in self.cs[ind].x])
print(msg)算法完成之后,当然要找个函数测试一下,测试函数为
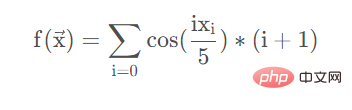
def test(xs):
_sum = 0.0
for i in range(len(xs)):
_sum = _sum + np.cos((xs[i]*i)/5)*(i+1)
return _sum
if __name__ == "__main__":
cNum = [15,20,100]
s = Swarm(cNum, 5, (-5,5))
s.optimize(test, 20, 5)测试结果如下
已经迭代4次,最佳优化结果为-5.793762423022024,参数为:
-6.599526, 3.117137, 5.959538, 7.225785, 5.204990
已经迭代9次,最佳优化结果为-10.61594651972434,参数为:
-7.003724, -5.589730, 0.981409, 12.920325, -19.006112
已经迭代14次,最佳优化结果为-9.143596747975293,参数为:
5.388234, -3.714421, -5.254391, -5.216215, -6.079223
已经迭代19次,最佳优化结果为-11.097888385616995,参数为:
-9.156244, -5.914600, -5.960154, 4.550833, 4.127889
已经迭代19次,最佳优化结果为-11.097888385616995,参数为:
-9.156244, -5.914600, -5.960154, 4.550833, 4.127889
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!