Réseau neuronal multi-graphique intégré

1. GNN d'un point de vue unifié

1. Paradigme de propagation GNN existant

Comment le GNN se propage-t-il dans l'espace aérien ? Comme le montre la figure ci-dessous, prenons le nœud A comme exemple :

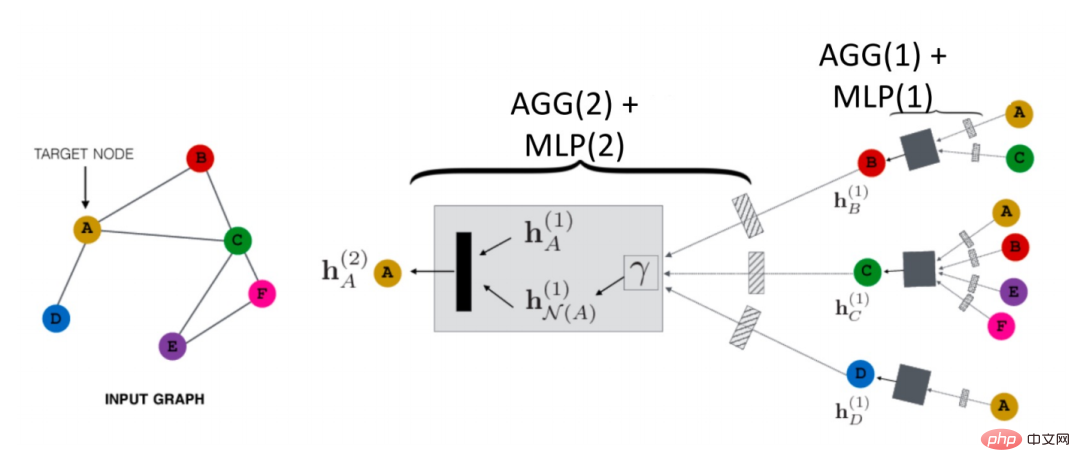
Il va d'abord agréger les informations de son nœud voisin N(A) en un seul h _{N( A)}⁽¹⁾, puis combiné avec la représentation de A de la couche supérieure h_N(A)⁽¹⁾ , puis passé grâce à une fonction de transformation (c'est-à-dire Trans(·) dans la formule), nous obtenons la représentation de niveau suivant de A h_N(A)⁽²⁾. Il s'agit du paradigme de propagation GCN le plus basique.

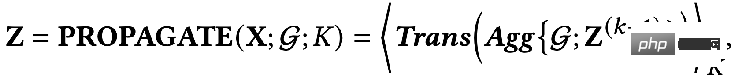
De plus, il existe un processus de propagation découplé :

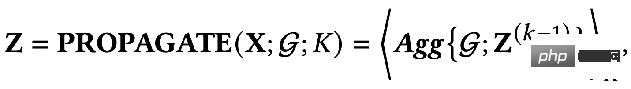
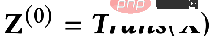
Quelle est la différence entre ces deux méthodes ? Dans le paradigme de propagation découplée, un extracteur de caractéristiques, c'est-à-dire la fonction de transformation, est d'abord utilisé pour extraire les caractéristiques initiales, puis les caractéristiques extraites sont placées dans la fonction d'agrégation pour l'agrégation. sont L'extraction et l'agrégation sont séparées, c'est-à-dire que le découplage est réalisé. L'avantage de ceci est :

• Vous pouvez librement concevoir la fonction de transformation précédente et utiliser n'importe quel modèle.
• De nombreuses couches peuvent être ajoutées lors de l'agrégation pour obtenir des informations de connexion à plus longue distance, mais nous ne serons pas confrontés au risque de surparamétrage car aucun paramètre ne doit être optimisé dans la fonction d'agrégation.

Ce qui précède sont les deux paradigmes principaux, et la sortie d'intégration du nœud peut utiliser la dernière couche du réseau ou le résidu de la couche intermédiaire.

Grâce à l'examen ci-dessus, nous pouvons voir qu'il existe deux sources d'informations de base dans GNN :

• La structure topologique du réseau : peut généralement capturer les diverses propriétés d'information de la structure du graphe.
• Caractéristiques des nœuds : Généralement, ils comprennent les signaux basse fréquence et haute fréquence des nœuds.

2. Un cadre d'optimisation unifié

Basé sur le mécanisme de propagation des GNN, nous pouvons constater que les GNN existants ont deux objectifs communs :

• Encodez les informations utiles à partir des caractéristiques des nœuds.
• Utilisez les capacités de lissage de la topologie.

Alors peut-on utiliser un langage mathématique pour décrire ces deux objectifs ? Quelqu'un a proposé le cadre unifié d'optimisation GNN suivant représenté par la formule : 🎜🎜#Le premier élément de l'objectif d'optimisation :

#🎜 🎜 #

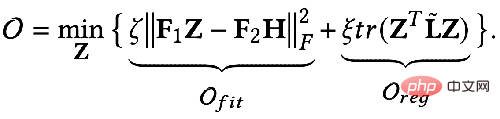
est un terme adapté aux fonctionnalités, son objectif est de rendre la représentation du nœud apprise Z aussi proche que possible de la fonctionnalité d'origine H, et F#🎜 🎜#1

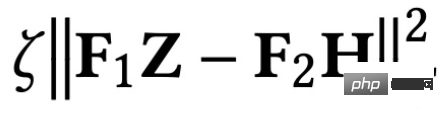
, F2# 🎜🎜# est un noyau de convolution graphique qui peut être conçu librement. Lorsque le noyau de convolution est la matrice identité I, cela équivaut à un filtre passe-tout ; lorsque le noyau de convolution est une matrice 0, c'est un filtre passe-bas, et lorsque le noyau de convolution est la matrice laplacienne L, c'est un filtre passe-bas. un filtre passe-haut. Le deuxième terme de l'objectif d'optimisation est formellement la trace d'une matrice, et sa fonction est de régulariser le graphique. Quelle est la relation entre les termes, les traces et la régularité ? En fait, le deuxième élément est développé sous la forme suivante : 🎜🎜 # _{Sa signification est de capturer le degré de différence de caractéristiques entre deux nœuds adjacents sur le graphique, ce qui représente la douceur d'un graphique. Minimiser cet objectif équivaut à nous rendre plus semblables à moi et à mon voisin.} 3. Utilisez un cadre d'optimisation unifié pour comprendre le GNN existant

#🎜🎜 #GNN optimise principalement cet objectif. Nous pouvons en discuter dans différentes situations :

lorsque les paramètres : #🎜🎜. #

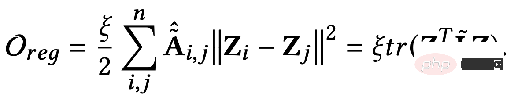
Quand l'objectif d'optimisation devient : # 🎜🎜##🎜🎜 #

Obtenir la dérivée partielle : # Comparons les résultats obtenus ci-dessus Après Pour une extension supplémentaire, vous pouvez obtenir : # Sa signification signifie que la représentation de tous les nœuds dans la Kème couche est égale au processus de propagation de la représentation des nœuds dans la K-1ème couche sur la matrice d'adjacence. Après dérivation jusqu'à la fin, on constatera qu'elle est égale à. la caractéristique initiale X. Après avoir terminé la transformation des caractéristiques W* Puis propagez K fois sur la matrice de contiguïté. En fait, il s'agit du modèle de GCN ou SGC avec la couche non linéaire supprimée.

Quand le paramètre F1=F

2

=I, ζ = 1, ξ=1/α-1, α∈(0,q], et lors de la sélection d'un filtre passe-tout, l'objectif d'optimisation devient :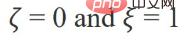

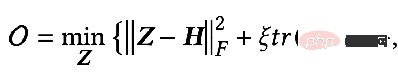
À ce moment, nous trouvons également la dérivée partielle de Z et fixons la dérivée partielle égale à 0 pour obtenir la solution fermée de l'objectif d'optimisation :

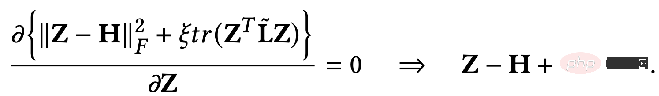
Transformez légèrement le résultat Vous pouvez obtenir la formule suivante :

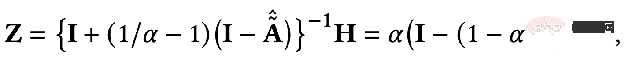
Nous pouvons constater que la formule ci-dessus représente le processus de propagation des fonctionnalités des nœuds sur le PageRank personnalisé, qui est le modèle PPNP.

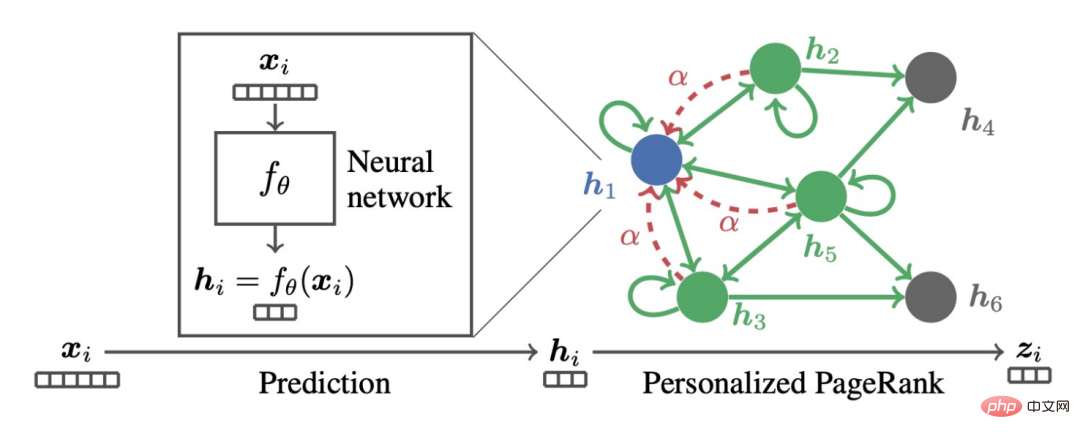
est également un tel modèle si vous utilisez la descente de gradient pour le trouver et définissez la taille du pas sur b, le terme d'itération est la dérivée partielle de la fonction objectif en Z au temps k-. 1.

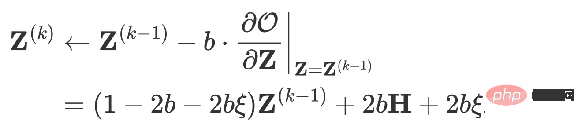
Quand vous obtenez :

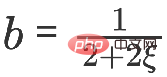
C'est le modèle APPNP. Le contexte de l'émergence du modèle APPNP est que le fonctionnement inverse de la matrice dans le modèle PPNP est trop compliqué et APPNP utilise une approximation itérative pour le résoudre. On peut également comprendre que l'APPNP peut converger vers le PPNP car les deux proviennent du même cadre.

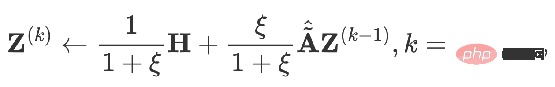
4. Nouveau cadre GNN

Tant que nous concevons un nouveau terme approprié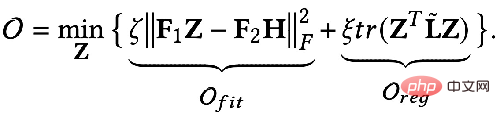

O

fit

et concevoir un correspondant Le graphique régulier Le terme Oreg, plus un nouveau processus de solution, peut obtenir un nouveau modèle GNN. ① Exemple 1 : Du filtrage passe-tout au filtrage passe-bas Comme mentionné précédemment, le noyau de convolution sous le filtre passe-tout

F

1

= F₂=I _{, lorsque le noyau de convolution est la matrice laplacienne L, c'est un filtre passe-haut. Si le GNN obtenu en pondérant ces deux situations peut coder une information passe-bas :} quand

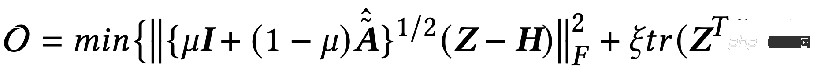
peut obtenir la solution exacte :

# 🎜🎜#

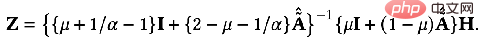
De même, nous pouvons le résoudre de manière itérative : 5, Elastic GNN

#🎜 🎜#

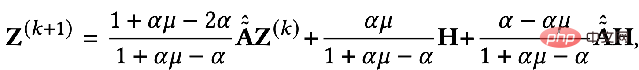Les termes réguliers mentionnés dans le cadre unifié précédent sont équivalents à L2 régulier , ce qui équivaut à calculer les informations de différence entre deux points quelconques du graphique. Certains chercheurs estiment que la régularisation L2 est trop globale et fera que la fluidité de l'ensemble du graphique aura tendance à être la même, ce qui n'est pas tout à fait cohérent avec la réalité. Par conséquent, il a été proposé d’ajouter un terme régulier L1 qui pénaliserait les changements relativement importants dans le graphique.

La partie régulière de L1 Pour :

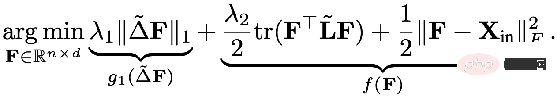
Bref, ce qui précède Ce cadre unifié nous dit :

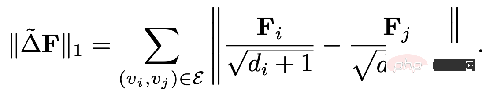
Nous pouvons utiliser une perspective plus macro pour comprendre GNN# 🎜 🎜#

Nous pouvons partir de ce cadre unifié pour concevoir un nouveau GNN

• #🎜🎜 # Cependant, ce cadre unifié ne peut être adapté qu'à des structures de graphes homogènes. Examinons ensuite la structure de graphe multi-relation plus courante.
• 2. Modèle GNN relationnel

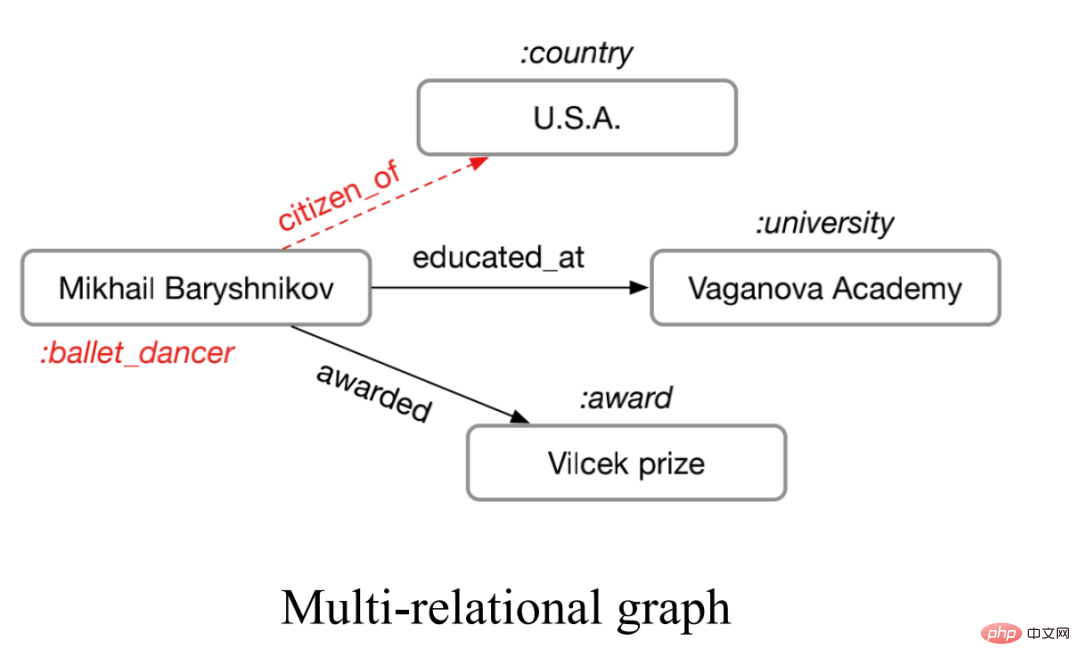
1, RGCN#🎜 🎜#Le graphe dit multi-relation fait référence à un graphe avec plus d'un type d'arête, comme le montre la figure ci-dessous.

Ce genre de multi-relation Le diagramme est très répandu dans le monde réel, comme les multiples types de liaisons moléculaires dans les molécules chimiques et les différentes relations entre les personnes dans les diagrammes de relations sociales. Pour de tels graphiques, nous pouvons utiliser des réseaux de neurones à graphes relationnels pour modéliser. L'idée principale est d'agréger individuellement des graphiques avec N relations pour obtenir N résultats d'agrégation, puis d'agréger les N résultats.

La formule est : #🎜 🎜#

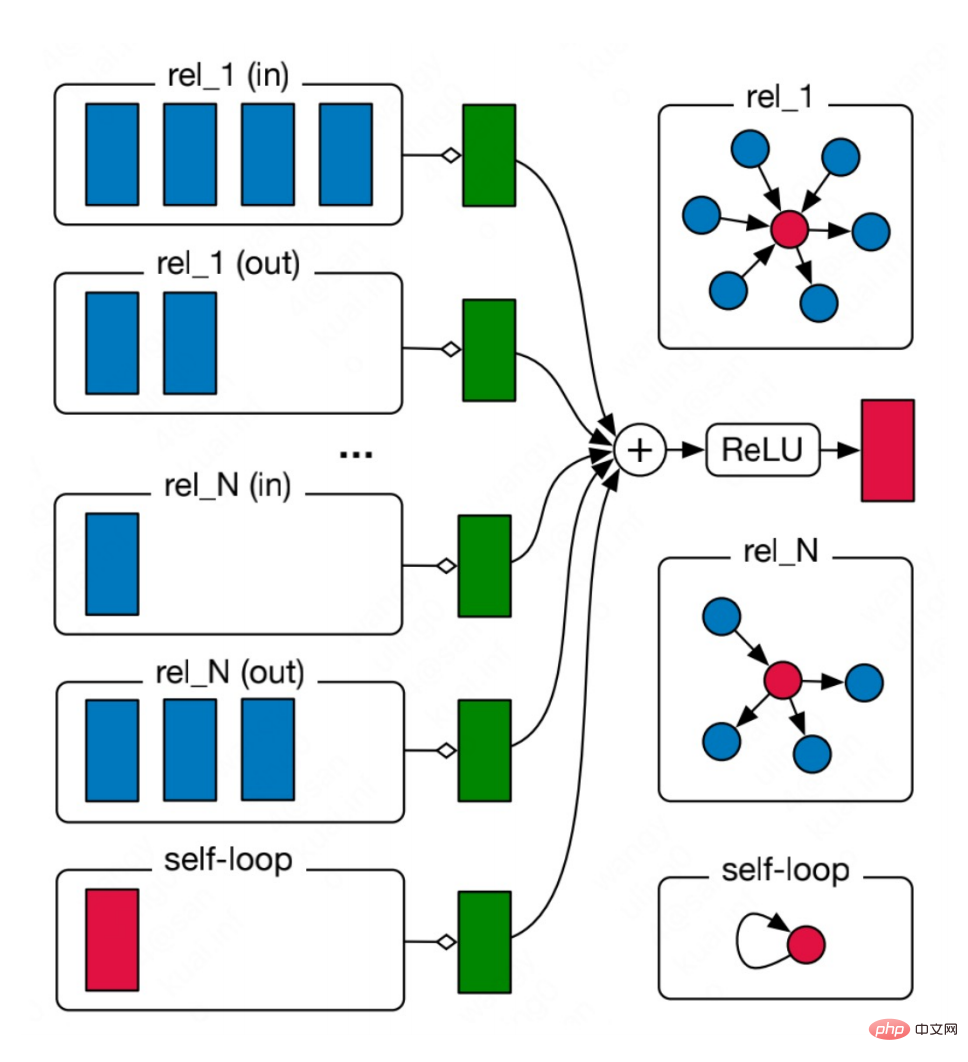
Vous pouvez voir que l'agrégation est divisée en deux étapes Pour continuer, sélectionnez d'abord une relation r parmi toutes les relations R, puis recherchez tous les nœuds contenant cette relation 🎜🎜#r

est agrégé, où

W

r

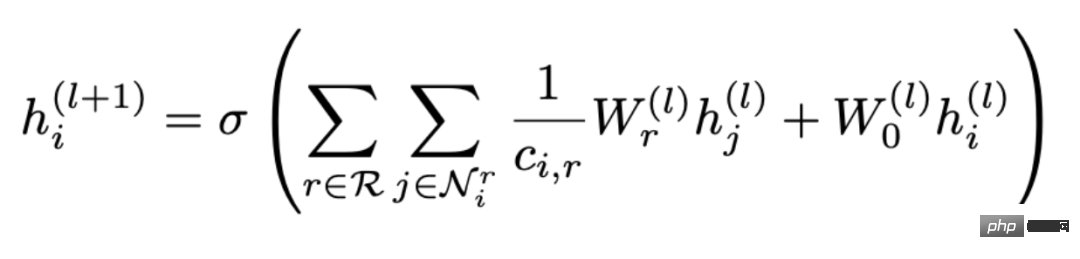
est le poids utilisé pour pondérer diverses relations. Par conséquent, vous pouvez voir qu'à mesure que le nombre de relations dans le graphique augmente, la matrice de poids Wr augmentera également, ce qui conduira au problème de la sur-paramétrage (Sur-paramétrage). De plus, diviser le diagramme de relations topologiques en fonction des relations peut également conduire à un lissage excessif.

2. CompGCN

Afin de résoudre le problème de surparamétrage, CompGCN utilise un encodeur relationnel vectorisé pour remplacer N matrices relationnelles :

L'encodeur contient des valeurs forward, reverse et relations en boucle automatique dans trois directions :

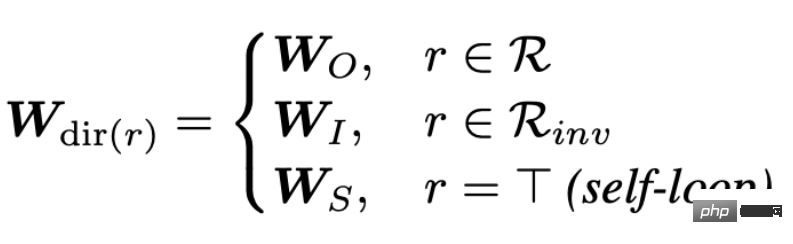
L'intégration de la relation sera également mise à jour à chaque itération.

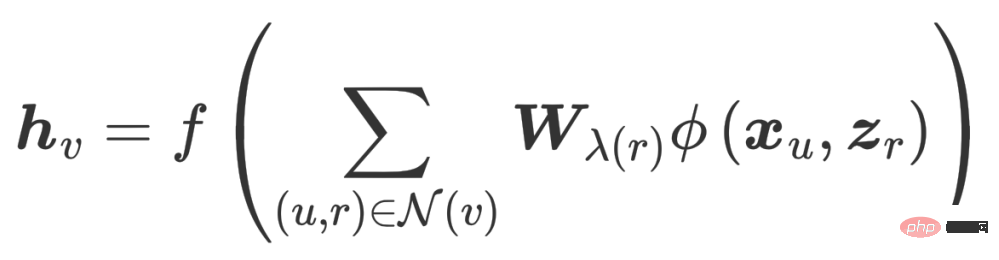
Mais cette conception heuristique et un tel encodeur paramétrique peuvent également provoquer un paramétrage excessif. Ensuite, sur la base des considérations ci-dessus, nous obtenons le point de départ de notre travail : pouvons-nous concevoir un GNN plus fiable du point de vue des objectifs d'optimisation, et en même temps résoudre les problèmes des GNN existants.

3. Intégration d'un réseau neuronal de graphes multi-relationnels

Notre EMR GNN a été publié cette année. Ensuite, nous discuterons principalement de la façon de concevoir un GCN adapté à plusieurs graphes de relations sous trois aspects :

. Comment concevoir un algorithme d'optimisation intégré approprié

• Ceci L'algorithme d'optimisation doit répondre à deux exigences :
• Être capable de capturer plusieurs relations sur le graphique en même temps
• Être capable de modéliser l'importance de différentes relations sur le graphique

Nous Le terme régulier du graphe multi-relation intégré proposé sur le graphe multi-relation est le suivant :

• Ce terme régulier sert également à capturer la capacité de lissage du signal du graphe, mais cette matrice d'adjacence est basée sur la relation r Capturé, et les paramètres soumis à des contraintes de normalisation
• μ
r

sont pour modéliser l'importance d'un certain relation. Le deuxième terme est la deuxième régularisation de forme normale du vecteur de coefficients, qui consiste à rendre le vecteur de coefficients plus uniforme.

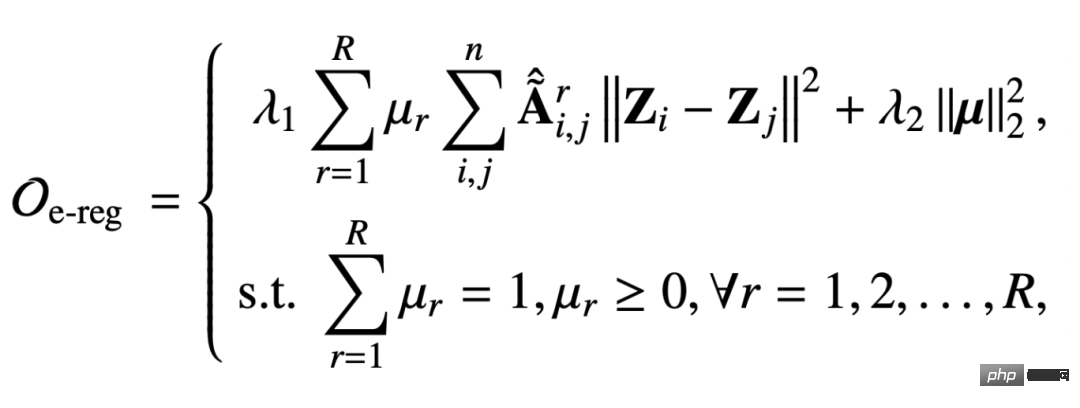
Afin de résoudre le problème du lissage excessif, nous avons ajouté un terme approprié pour garantir que les informations sur les fonctionnalités d'origine ne soient pas perdues. La somme du terme approprié et du terme régulier est : Par rapport au cadre unifié mentionné dans le chapitre précédent, la fonction objectif que nous avons conçue ici comprend deux paramètres de correction de nœud Z et de matrice de relation μ variable. C'est donc également un défi de dériver un mécanisme de propagation de message basé sur un tel objectif d'optimisation.

2. Dérivation du mécanisme de passage des messages

Ici on adopte une stratégie d'optimisation itérative : #🎜🎜 #

• Corrigez d'abord la représentation du nœud Z, puis optimisez le paramètre μ#🎜🎜 #
• Selon le résultat μ de l'itération précédente, optimiser la représentation des nœuds Z

#🎜🎜 # Lorsque le nœud fixe représente Z, tout l'objectif d'optimisation dégénère en une fonction objectif liée uniquement à μ, mais il s'agit d'une fonction objectif contrainte :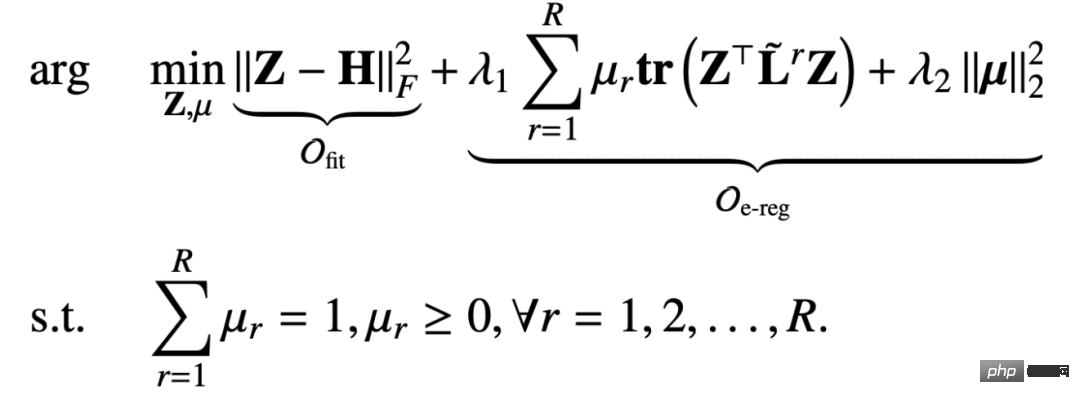

#🎜 🎜#

Il s'agit en fait d'une fonction convexe de μ sur une contrainte simplexe (contrainte dans un simplexe standard). Algorithme de descente entropique miroir pour résoudre ce problème. Nous trouverons d'abord une constante, puis mettrons à jour le coefficient de poids sous chaque relation. L'ensemble du processus de mise à jour est similaire à l'algorithme de descente de gradient exponentiel.

Coefficient de relation fixe μ Aller à mise à jour Z, l'objectif d'optimisation à ce moment dégénère sous la forme suivante : #

De cette façon, nous trouvons la dérivée partielle de la fonction objectif par rapport à Z et fixons la dérivée partielle égale à 0 pour obtenir : # 🎜🎜#

Alors la solution de forme fermée de Z est :

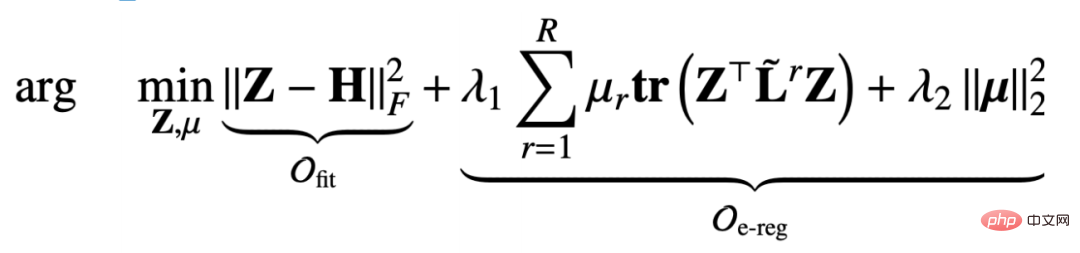
#🎜 De la même manière, nous pouvons utiliser l'itération pour obtenir une solution approximative. exprimé comme suit : # À partir du mécanisme de transmission de messages dérivé, nous pouvons prouver que cette conception peut éviter un lissage excessif et un paramétrage excessif. Ci-dessous, nous pouvons examiner le processus de preuve.

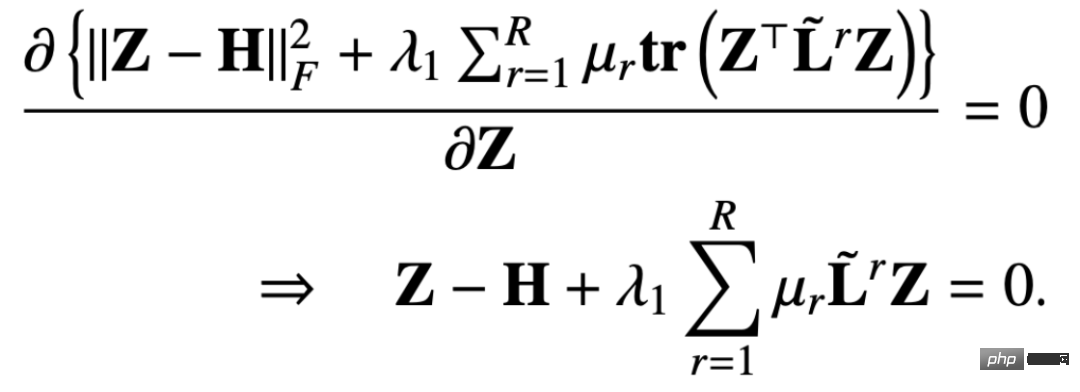La matrice PageRank multi-relation originale est définie comme suit :

#🎜🎜 #

La matrice PageRank multi-relation personnalisée ajoute une probabilité de renvoyer son propre nœud sur cette base : # En résolvant l'équation de boucle ci-dessus, vous pouvez obtenir la matrice PageRank personnalisée multi-relation : #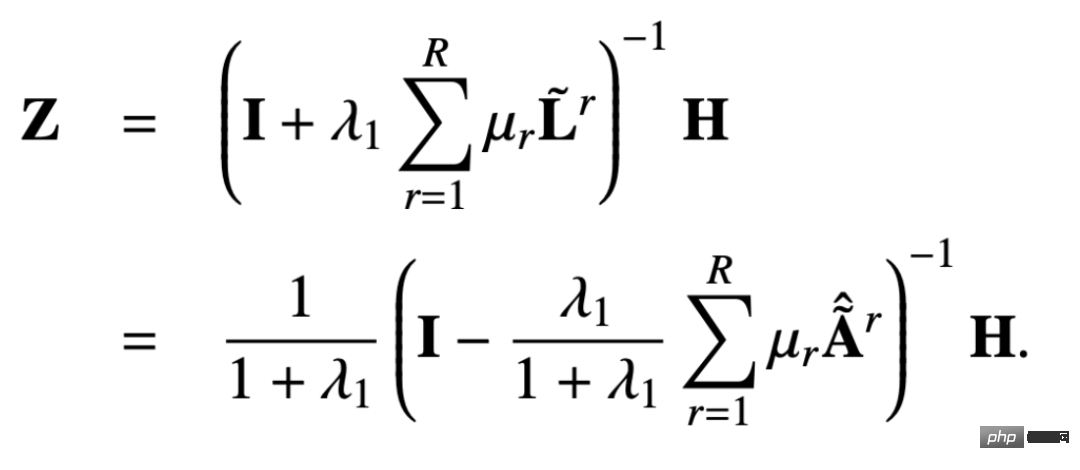

On laisse :

peut être obtenu :

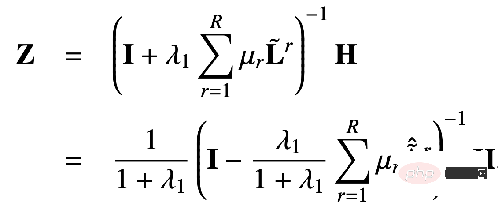
C'est la solution de forme fermée obtenue par notre solution proposée. C'est-à-dire que notre mécanisme de propagation peut être équivalent à propager la fonctionnalité H sur la matrice PageRank personnalisée du nœud. Parce que dans ce mécanisme de propagation, un nœud peut revenir à son propre nœud avec une certaine probabilité, ce qui signifie que ses propres informations ne seront pas perdues pendant le processus de transmission des informations, évitant ainsi le problème de lissage excessif.

De plus, notre modèle atténue également le phénomène de sur-paramétrisation, car comme vous pouvez le voir sur la formule, notre modèle n'a qu'un seul coefficient apprenable pour chaque relation μ _r , par rapport à l'encodeur précédent, ou à la matrice de poids w_r Par rapport au nombre de paramètres, l'ampleur de nos paramètres est presque négligeable. La figure suivante montre l'architecture du modèle que nous avons conçue :

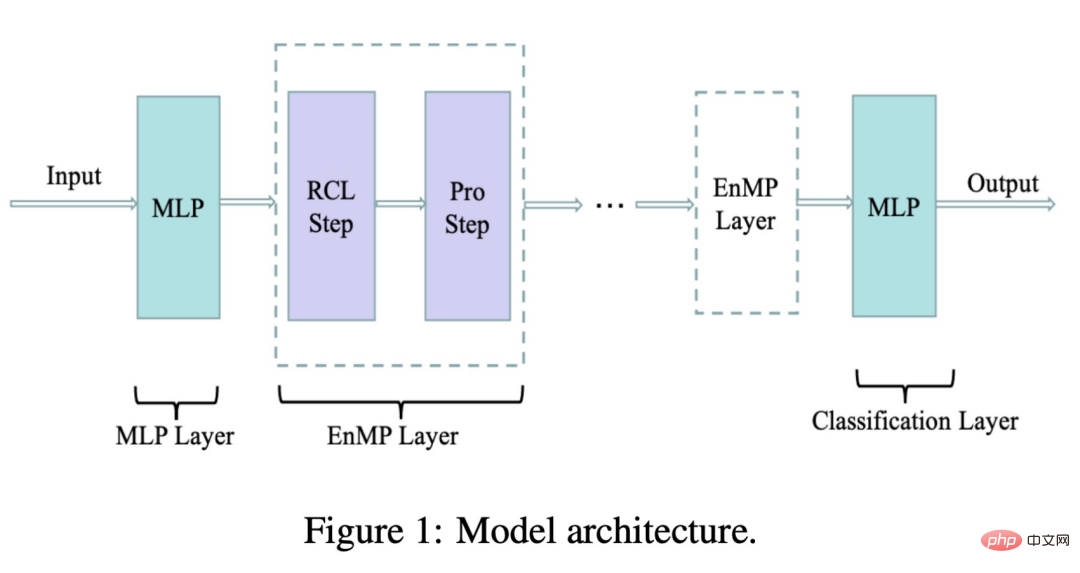
où RCL est l'étape d'apprentissage des paramètres et l'étape Pro est l'étape de propagation des fonctionnalités. Ces deux étapes forment ensemble notre couche de messagerie. Alors, comment intégrer notre couche de messagerie dans le DNN sans introduire davantage de paramètres supplémentaires ? Nous suivons également l'idée de conception du découplage : utilisez d'abord un MLP pour extraire les caractéristiques d'entrée, puis passez à travers plusieurs couches de transmission de messages que nous avons conçues. La superposition de plusieurs couches n'entraînera pas un lissage excessif. Le résultat final du transfert est traité par MLP pour compléter la classification des nœuds et peut être utilisé pour les tâches en aval. Le processus ci-dessus est représenté par la formule suivante :

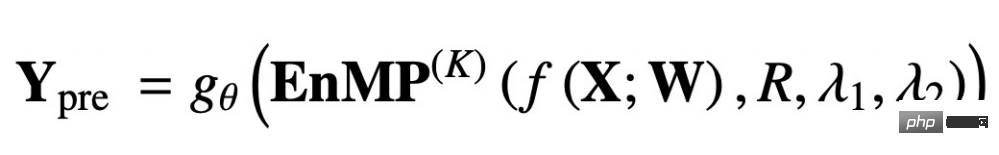
f(X;W) signifie que les entités en entrée sont extraites via MLP, et l'EnMP(K) suivant signifie que les résultats de l'extraction sont transmis à travers K couches. Le message passant, g_θ représente un MLP classifié.

En rétropropagation, il nous suffit de mettre à jour les paramètres dans les deux MLP, et les paramètres de notre EnMP sont appris pendant le processus de propagation vers l'avant. Il n'est pas nécessaire de mettre à jour un paramètre EnMP pendant le processus de propagation vers l'arrière. .

Nous pouvons comparer les paramètres de différents mécanismes. Nous pouvons voir que les paramètres de notre EMR-GNN proviennent principalement des deux MLP avant et après, et du coefficient de relation. Lorsque le nombre de couches est supérieur à 3, on peut savoir que le nombre de paramètres d'EMR-GNN est inférieur à celui de GCN, et même inférieur à celui des autres graphes hétérogènes.

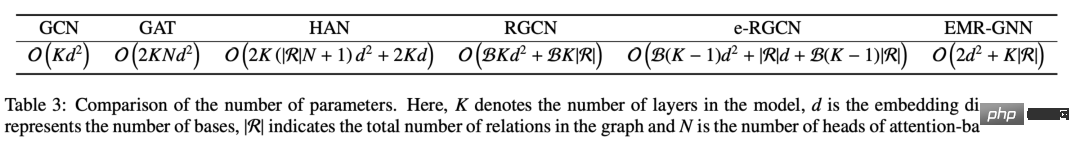
Avec un si petit nombre de paramètres, notre EMR-GNN peut toujours atteindre le meilleur niveau sous différentes tâches de classification de nœuds comme suit.

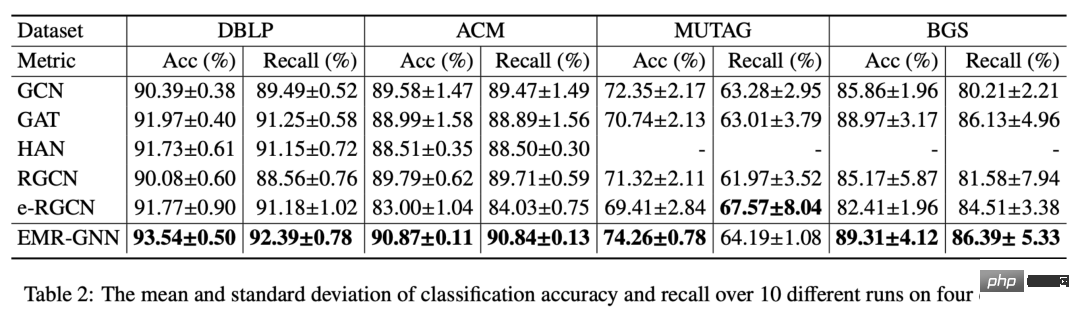
De plus, nous avons également comparé les changements dans la précision de la classification de différentes structures de réseau après l'augmentation du nombre de couches, lorsque le nombre de couches augmente à 64, notre modèle peut toujours maintenir une grande précision, tout en. le RGCN d'origine rencontrera une mémoire insuffisante lorsque le nombre de couches passe à plus de 16, et il est impossible de superposer plus de couches. Cela est dû à un trop grand nombre de paramètres. Les performances du modèle GAT sont dégradées en raison d'un lissage excessif.

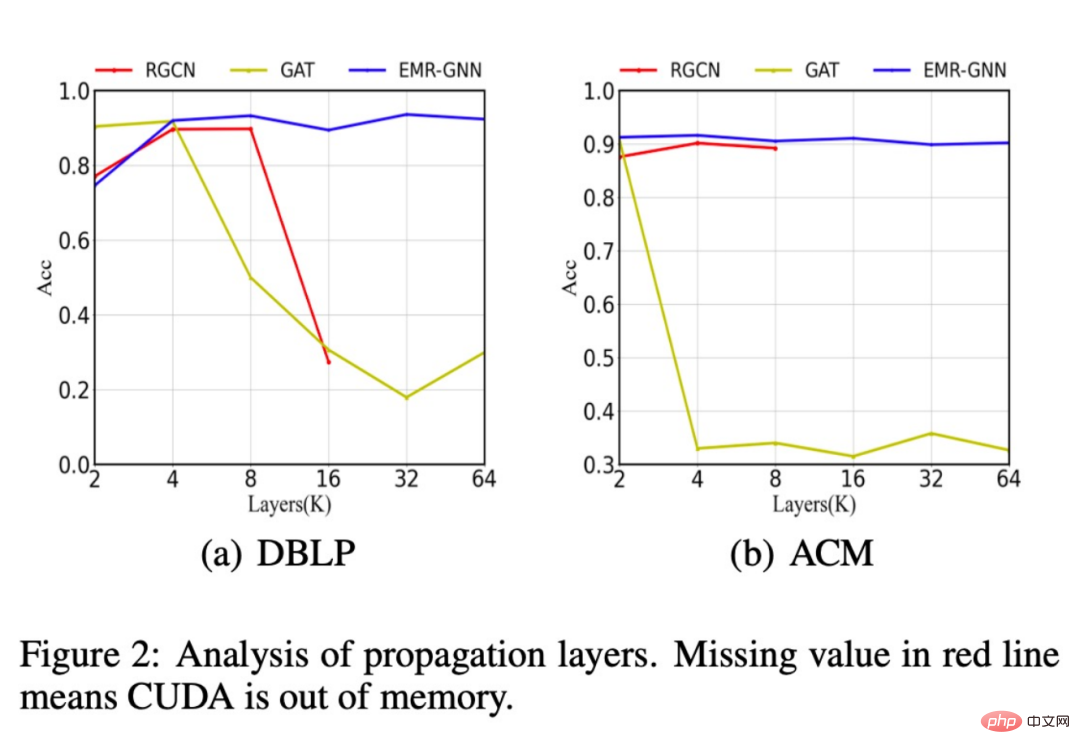
De plus, nous avons également constaté que notre EMR-GNN peut atteindre la précision de classification de l'échantillon complet avec une taille de données plus petite, tandis que le RGCN chute beaucoup.

Nous avons également analysé si le coefficient de relation μr appris par EMR-GNN est vraiment significatif, alors qu'est-ce qui est significatif ? Nous souhaitons que le coefficient de relation accorde plus de poids aux relations importantes et moins de poids aux relations sans importance. Les résultats de notre analyse sont présentés dans la figure ci-dessous : L'histogramme vert représente l'effet de la classification sous une relation. Si la précision de la classification est plus élevée sous une certaine relation, nous le ferons. peut être considéré comme important. Les colonnes bleues représentent les coefficients de relation appris par notre EMR-GNN. La comparaison entre le bleu et le vert montre que notre coefficient de relation peut refléter l'importance de la relation.

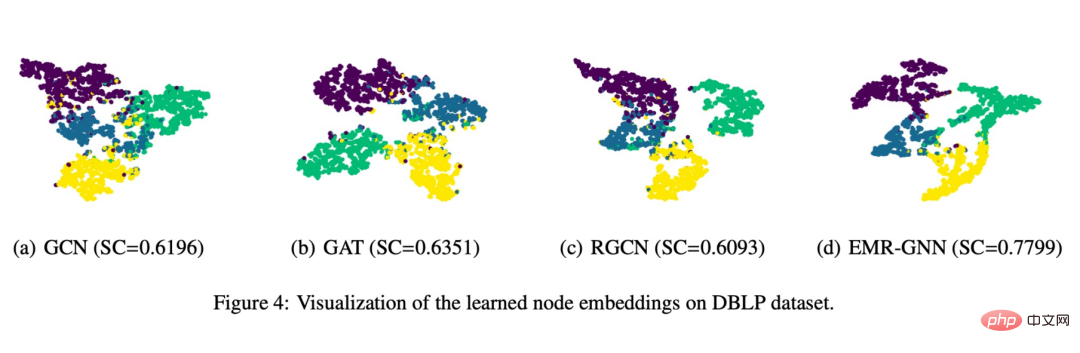
Enfin, nous avons également réalisé un affichage visuel comme le montre la figure ci-dessous :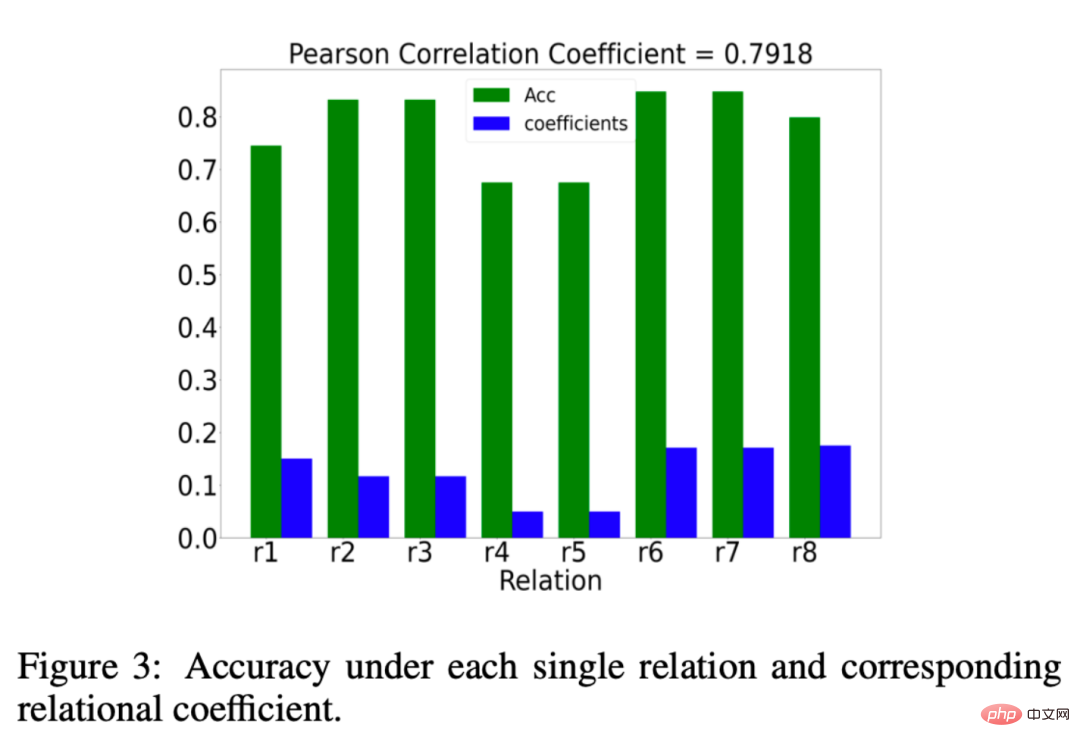

Vous pouvez voir que l'intégration de nœuds formée par EMR-GNN peut transporter les informations structurées de Le nœud. Il peut rendre les nœuds du même type plus cohérents, séparer autant que possible les différents types de nœuds et rendre les limites de segmentation plus claires que les autres réseaux.

4. Résumé

1. Nous utilisons une perspective unifiée pour comprendre le GNN

① De cette perspective, nous pouvons facilement voir quels sont les problèmes avec les GNN existants

② ceci Une perspective unifiée peut nous donner une base pour repenser GNN

2 Nous essayons de concevoir un nouveau GNN multi-relationnel du point de vue de la fonction objectif

① Nous concevons d'abord un cadre d'optimisation intégré

.

② Basé sur un tel cadre d'optimisation, nous avons dérivé un mécanisme de transmission de messages

③ Ce mécanisme de transmission de messages avec un petit nombre de paramètres est simplement combiné avec MLP pour obtenir EMR-GNN

3. Quels sont les avantages du DME-GNN ?

① Elle s'appuie sur un objectif d'optimisation fiable, donc les résultats obtenus sont crédibles, et ses principes sous-jacents peuvent être expliqués mathématiquement

② Elle peut résoudre le problème de sur-lissage de la relation GNN existante

③ Résolu le problème de paramétrage

④ Facile à entraîner, de meilleurs résultats peuvent être obtenus avec des paramètres plus petits

5. Séance de questions-réponses

Q1 : Y a-t-il une différence entre l'apprentissage des coefficients relationnels et le mécanisme d'attention ?

A1 : L'apprentissage du coefficient de relation est ici un processus de mise à jour dérivé du cadre d'optimisation, tandis que l'attention est un processus qui doit être appris sur la base de la rétropropagation, les deux sont donc essentiellement différents en termes d'optimisation.

Q2 : Quelle est l'applicabilité du modèle sur des ensembles de données à grande échelle ?

A2 : Nous avons analysé la complexité du modèle en annexe. En terme de complexité, nous sommes au même niveau que RGCN, mais le nombre de paramètres sera plus petit que RGCN, donc notre modèle est plus adapté. ensemble de données à grande échelle.

Q3 : Ce cadre peut-il intégrer des informations de pointe ?

A3 : Peut être intégré au terme approprié ou au terme régulier.

Q4 : Où dois-je apprendre ces bases mathématiques ?

A4 : Une partie est basée sur des travaux antérieurs, et l'autre partie de la théorie mathématique liée à l'optimisation est également utilisée par certains articles d'optimisation plus classiques.

Q5 : Quelle est la différence entre un diagramme de relations et un diagramme hétérogène ?

A5 : Le graphe de relations est un graphe hétérogène, mais nous considérons généralement les graphes hétérogènes comme ceux dont les types de nœuds ou les types d'arêtes sont supérieurs à 1. Dans le diagramme de relations, nous nous intéressons particulièrement à la catégorie de relation supérieure à 1. On comprend que cette dernière inclut la première.

Q6 : Peut-il prendre en charge la formation en mini-batch ?

A6 : Prise en charge.

Q7 : L'orientation future de la recherche du GNN est-elle plus encline à une dérivation mathématique stricte et interprétable qu'à une conception heuristique ?

A7 : Nous pensons nous-mêmes que la dérivation mathématique strictement interprétable est une méthode de conception fiable.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!