Comment utiliser Python pour trouver la norme et le déterminant d'une matrice

Dans la fonction de scipy.linalg, deux paramètres sont souvent fournis. L'un est check_finite. Lorsqu'il est True, une vérification limitée sera. effectué , l'autre type est overwrite_xxxx, qui indique si xxxx peut être écrasé pendant le processus de calcul. Par souci de simplicité, nous dirons plus tard que a fournit un commutateur d'écrasement, ce qui signifie qu'il existe un paramètre overwrite_a lorsqu'il est Truecode>, a permet que le processus de calcul soit remplacé ; si un commutateur de vérification limité est fourni, cela signifie que le paramètre <code>check_finite est fourni. scipy.linalg的函数中，往往会提供两种参数，其一是check_finite，当为True时将进行有限检查，另一类是overwrite_xxxx，表示xxxx在计算过程中是否可以被覆写。简洁起见，后文中说a提供覆写开关，就表示存在一个参数overwrite_a，当其为True时，a允许计算过程中被覆写；若说提供有限检查开关，则代表提供check_finite参数。

范数

在scipy.linalg中提供了函数norm用来求范数，其定义为

norm(a, ord=None, axis=None, keepdims=False, check_finite=True)

其中ord用于声明范数的阶

ord	矩阵范数	向量范数
None	弗罗贝尼乌斯范数	2-范数
'fro'	弗罗贝尼乌斯范数	-
'nuc'	核范数	-
inf	max(sum(abs(a), axis=1))	max ⁡ ( ∣ a ∣ )
-inf	min(sum(abs(a), axis=1))	min ⁡ ( ∣ a ∣ )
0	-	sum(a!=0)
1	max(sum(abs(a), axis=0))
-1	min(sum(abs(a), axis=0))
2	2-范数(最大奇异值)
-2	最小奇异值

若a为向量，若ord为非零整数，记作n nn，设a i a_iai为矩阵a aa中的元素，则矩阵的n nn范数为

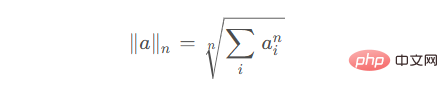
核范数又称“迹范数” (trace norm)，表示矩阵的所有奇异值之和。

Frobenius范数可定义为

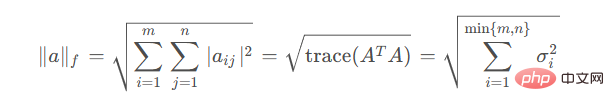
其实质是向量的2-范数在矩阵中的自然推广。

除了scipy.linalg之外，numpy.linalg中也提供了norm，其参数为

norm(x, ord=None, axis=None, keepdims=False)

其中order的可选参数与scipy.linalg中的norm函数相同。

行列式

在scipy.linalg中，行列式函数为det，其定义非常简单，除了待求矩阵a之外，就只有a的覆写开关和有限检查。

示例如下

import numpy as np
from scipy import linalg
a = np.array([[1,2,3], [4,5,6], [7,8,9]])
linalg.det(a)
# 0.0
a = np.array([[0,2,3], [4,5,6], [7,8,9]])
linalg.det(a)
# 3.0

迹

scipy.linalg不提供trace函数，但是numpy提供，其定义为

umpy.trace(a, offset=0, axis1=0, axis2=1, dtype=None, out=None)

其中

• offset为偏移量，表示相对于主对角线的偏移

• axis1, axis2 表示坐标轴

• dtype

  Norm

  La fonction norm est fournie dans scipy.linalg pour trouver la norme, qui est définie comme

>>> x = np.random.rand(3,3)
>>> print(x)
[[0.26832187 0.64615363 0.09006217]
 [0.63106319 0.65573765 0.35842304]
 [0.66629322 0.16999836 0.92357658]]
>>> np.trace(x)
1.8476361016546932

où ord est utilisé pour déclarer l'ordre de la norme 🎜 tr>max(sum(abs(a), axis=0))

ord	Norme matricielle	Norme vectorielle Numéro
		td>
Aucun	Norme Frobenius	Norme 2
'fro'	Norme Frobenius	-
'nuc'	Norme nucléaire	-
inf	max(sum( abs(a), axis=1))	max ⁡ ( ∣ a ∣ )
-inf	min(somme(abs(a), axis=1))	min ⁡ ( ∣ a ∣ )
0	-	somme(a!=0)
1	td>
-1	min(sum(abs(a), axis=0))
2	2-norme (valeur singulière maximale)
-2	Valeur singulière minimale

🎜 Si a est un vecteur Si ord est un entier non nul, il est enregistré sous la forme n nn. Soit a i a_iai les éléments de la matrice a aa, alors la norme n nn de la matrice est 🎜 🎜<img src="https://img.php.cn/upload/article/000/887/227/168373140984473.png" alt="Comment utiliser Python pour trouver la norme et le déterminant d'une matrice">🎜🎜kernel La norme, aussi connue sous le nom de « norme de trace », représente la somme de toutes les valeurs singulières de la matrice. 🎜🎜La norme Frobenius peut être définie comme🎜🎜<img src="https://img.php.cn/upload/article/000/887/227/168373140928434.png" alt="Comment utiliser Python pour trouver la norme d'une matrice et d'un déterminant">🎜🎜L'essence est la généralisation naturelle de la norme 2 des vecteurs dans les matrices. 🎜🎜En plus de <code>scipy.linalg, numpy.linalg fournit également norm, dont les paramètres sont 🎜rrreee🎜où order L'optionnel les paramètres de sont les mêmes que ceux de la fonction norm dans scipy.linalg. 🎜

Déterminant

🎜Dans scipy.linalg, la fonction déterminante est det, et sa définition est très simple, à l'exception de la matrice à trouver a En dehors de , il n'y a que des commutateurs de remplacement et des vérifications limitées de a. 🎜🎜L'exemple est le suivant🎜rrreee

trace

🎜scipy.linalg ne fournit pas la fonction trace, mais numpy fait, et sa définition est 🎜rrreee🎜où 🎜
• 🎜offset est le décalage, indiquant le décalage par rapport à la diagonale principale 🎜🎜
• 🎜axis1, axis2 représente l'axe des coordonnées🎜🎜
• 🎜dtype est le type de données utilisé pour ajuster la valeur de sortie🎜🎜🎜rrreee

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!