Comment dessiner un diagramme circulaire double avec des lignes de connexion en Python

1. Importez les bibliothèques requises

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import ConnectionPatch
from matplotlib import cm

La classe ConnectionPatch du module matplotlib.patches peut être utilisée pour établir la connexion entre deux sous-intrigues. Dans des visualisations telles qu'un diagramme circulaire double, vous pouvez utiliser cette classe pour établir une connexion entre deux sous-graphiques afin d'exprimer la relation entre eux. Cette classe fournit de nombreux paramètres et méthodes pouvant être utilisés pour contrôler des propriétés telles que le style et la position de la connexion.

ConnectionPatch est utilisé pour ajouter des connexions dans Matplotlib. Ses principaux paramètres sont les suivants :

• xyA : le point de départ de la ligne de connexion ;

• xyB : le point final de la ligne de connexion ; coordsA : le système de coordonnées du point de départ, la valeur par défaut est data ;

• coordsB : le système de coordonnées du point final, la valeur par défaut est data

• axesA : objet Axes où se trouve le point de départ ; Objet Axes où se trouve le point final ;

• color : la couleur de la ligne de connexion ;

• linewidth : la largeur de la ligne de connexion ;

• linestyle : le style de ligne de la ligne de connexion ;

• Les méthodes couramment utilisées de ConnectionPatch incluent :

• set_color : définissez la couleur de la ligne de connexion ;

set_linewidth : définissez la largeur de la ligne ; la ligne de connexion ;

• set_linestyle : Définissez le style de ligne de la ligne de connexion. set_color：设置连接线的颜色；

• set_linewidth：设置连接线的线宽；

• set_linestyle：设置连接线的线型。

cm是Matplotlib的颜色映射模块，它提供了一系列的颜色方案，包括了单色调，分段调色和连续渐变调色等多种颜色方案，能够更好的满足数据可视化中的需求。

二、准备数据

# 大饼图数据
labels = ['301', '302', '303', '304', '305', '307', '308', '306']
size = [219324, 94739, 75146, 71831, 54051, 21458, 9990, 50843]
# 大饼图分裂距离
explode = (0, 0, 0, 0, 0, 0, 0, 0.1)
# 小饼图数据
labels2 = ['402', '407']
size2 = [12255, 207069]
width = 0.2

这段代码用于定义大饼图和小饼图的数据，并设置大饼图的分裂距离和小饼图的宽度。

具体解释如下：

• labels：定义大饼图每个分裂块的标签，即分别表示哪个区域。

• size：定义大饼图每个分裂块的大小，即表示每个区域的数量或占比。

• explode：定义大饼图每个分裂块距离饼心的距离，即分裂块是否需要弹出，这里设置为不弹出。

• labels2：定义小饼图每个分裂块的标签，即分别表示哪个区域。

• size2：定义小饼图每个分裂块的大小，即表示每个区域的数量或占比。

• width：定义小饼图的宽度，这里设置为0.2。

三、绘制双饼图

3.1 创建画布和子图对象

fig = plt.figure(figsize=(9, 5))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)

这部分代码创建了一个大小为 (9, 5) 的画布 fig，并在该画布上添加了两个子图 ax1 和 ax2。

其中，fig.add_subplot(121) 表示将画布分为 1 行 2 列的子图，选择第 1 个子图（即左边的子图）；fig.add_subplot(122)

cm est le module de cartographie des couleurs de Matplotlib. Il fournit une série de schémas de couleurs, notamment un ton unique, une coloration segmentée et une coloration en dégradé continu, etc., qui peuvent mieux répondre aux besoins de visualisation des données.

2. Préparer les données

ax1.pie(size,
        autopct='%1.1f%%',
        startangle=30,
        labels=labels,
        colors=cm.Blues(range(10, 300, 50)),
        explode=explode)

• Ce code est utilisé pour définir les données du grand diagramme circulaire et du petit diagramme circulaire, et définir la distance de séparation du grand diagramme circulaire et la largeur du petit diagramme circulaire.
  L'explication spécifique est la suivante :

• étiquettes : définissez les étiquettes de chaque bloc divisé du diagramme circulaire, c'est-à-dire quelle zone chacun représente.

• taille : définissez la taille de chaque bloc divisé du diagramme circulaire, c'est-à-dire le nombre ou la proportion de chaque zone.

• exploser : définissez la distance entre chaque bloc divisé du grand diagramme circulaire et le centre du secteur, c'est-à-dire si le bloc divisé doit apparaître, ici, il est configuré pour ne pas apparaître.

• labels2 : Définissez l'étiquette de chaque bloc divisé du petit diagramme circulaire, c'est-à-dire la zone qu'il représente.

• size2 : Définissez la taille de chaque bloc divisé du petit diagramme circulaire, ce qui signifie le nombre ou la proportion de chaque zone.

width : Définissez la largeur du camembert, ici définie sur 0,2.

3. Dessinez un diagramme circulaire double

• 3.1 Créer des objets de canevas et de sous-figures

  ax2.pie(size2,
          autopct='%1.1f%%',
          startangle=90,
          labels=labels2,
          colors=cm.Blues(range(10, 300, 50)),
          radius=0.5,
          shadow=False)

  Cette partie du code crée une figure de canevas d'une taille de (9, 5) et ajoute deux sous-figures ax1 et ax2.
• Parmi eux, fig.add_subplot(121) signifie diviser le canevas en sous-intrigues avec 1 ligne et 2 colonnes, et sélectionner la première sous-intrigue (c'est-à-dire la sous-intrigue de gauche) fig. add_subplot( 122) signifie sélectionner la deuxième sous-image (c'est-à-dire la sous-image à droite). La règle de numérotation du sous-graphe est similaire à l'index du tableau. Le numéro de ligne augmente de 1 de haut en bas et le numéro de colonne augmente de 1 de gauche à droite. Par exemple, (1, 1) représente le sous-graphe du premier. ligne et première colonne, ( 1, 2) représente le sous-graphe de la première ligne et de la deuxième colonne. Ici, 121 et 122 représentent respectivement le premier et le deuxième sous-graphes de la première ligne.
  3.2 Dessiner un grand diagramme circulaire

theta1, theta2 = ax1.patches[-1].theta1, ax1.patches[-1].theta2
center, r = ax1.patches[-1].center, ax1.patches[-1].r
x = r * np.cos(np.pi / 180 * theta2) + center[0]
y = np.sin(np.pi / 180 * theta2) + center[1]
con1 = ConnectionPatch(xyA=(0, 0.5),
                       xyB=(x, y),
                       coordsA=ax2.transData,
                       coordsB=ax1.transData,
                       axesA=ax2, axesB=ax1)

• Ce code est utilisé pour dessiner un diagramme circulaire dans le premier sous-graphique (ax1). La signification des paramètres spécifiques est la suivante :

• size : données du graphique à secteurs, indiquant la taille de chaque bloc du graphique à secteurs.

• autopct : Le format d'étiquette de données du bloc de diagramme circulaire, "%1.1f%%" signifie conserver une décimale et ajouter un signe de pourcentage.

• startangle : L'angle de départ du diagramme circulaire, 30 degrés est le point de départ, tournez dans le sens des aiguilles d'une montre.

• étiquettes : étiquettes de blocs de diagramme circulaire, correspondant à la taille.
  🎜🎜colors : Les couleurs des blocs du diagramme circulaire, en utilisant la fonction cm.Blues() pour générer une liste de couleurs. 🎜🎜🎜🎜exploser : La distance de division du bloc du diagramme circulaire, indiquant s'il est séparé du centre du diagramme circulaire. Par exemple, (0, 0, 0, 0, 0, 0, 0, 0,1) signifie que le dernier morceau de tarte est à 0,1 rayon du centre. 🎜🎜🎜🎜Ces paramètres et ceux d'autres diagrammes circulaires peuvent être ajustés selon les besoins pour obtenir l'effet souhaité. 🎜🎜3.3 Dessiner un diagramme circulaire🎜

  x = r * np.cos(np.pi / 180 * theta1) + center[0]
  y = np.sin(np.pi / 180 * theta1) + center[1]
  con2 = ConnectionPatch(xyA=(-0.1, -0.49),
                         xyB=(x, y),
                         coordsA='data',
                         coordsB='data',
                         axesA=ax2, axesB=ax1)

  🎜Ce code est utilisé pour dessiner le deuxième diagramme circulaire. Les significations spécifiques des paramètres sont les suivantes : 🎜🎜🎜🎜size2 : les données du petit diagramme circulaire, c'est-à-dire [12255, 207069] ; 🎜🎜🎜🎜autopct : l'étiquette de données du bloc formaté en forme de coin, « %1.1f%%’ signifie réservé Une décimale, suivie d'un signe pour cent 🎜🎜🎜🎜startangle : l'angle de départ du diagramme circulaire, exprimé en degrés, ici fixé à 90 degrés, c'est-à-dire en partant de la verticale ; direction ; 🎜🎜🎜🎜labels2 : L'étiquette du petit diagramme circulaire, à savoir [‘402’, «407’] ; 🎜🎜🎜🎜colors : Spécifiez la couleur, ici la fonction cm.Blues est utilisée pour générer un ensemble de couleurs de la série bleue ; 🎜🎜🎜🎜radius : petit gâteau Le rayon de l'image, ici est défini sur 0,5 ; 🎜🎜🎜🎜shadow : s'il faut ajouter une ombre, ici est défini sur False. 🎜

在这段代码中，我们创建了一个名为 ax2 的子区域对象，并使用 pie 方法绘制了一个小饼图，将 size2 中的数据作为输入数据。其他参数指定了锲形块的格式、颜色、标签等属性，进一步定制了图形的样式。

3.4 连接线1，连接大饼图的上边缘和小饼图的饼块

theta1, theta2 = ax1.patches[-1].theta1, ax1.patches[-1].theta2
center, r = ax1.patches[-1].center, ax1.patches[-1].r
x = r * np.cos(np.pi / 180 * theta2) + center[0]
y = np.sin(np.pi / 180 * theta2) + center[1]
con1 = ConnectionPatch(xyA=(0, 0.5),
                       xyB=(x, y),
                       coordsA=ax2.transData,
                       coordsB=ax1.transData,
                       axesA=ax2, axesB=ax1)

这部分代码是用来计算连接两个饼图的连接线的起点和终点位置，并创建一个 ConnectionPatch 对象用于绘制连接线。

• theta1 和 theta2 分别表示饼图上最后一个扇形的起始角度和终止角度。

• center 表示饼图中最后一个扇形的中心点位置。

• r 表示饼图的半径。

• x 和 y 表示连接线的终点坐标，其中 x 通过利用三角函数计算出来。

接下来，ConnectionPatch 的参数解释：

• xyA 表示连接线的起点位置，这里设为 (0, 0.5) 表示在小饼图上以它的左边中间位置为起点。

• xyB 表示连接线的终点位置，这里为 (x, y) 表示在大饼图上以计算得到的 x 和 y 为终点位置。

• coordsA 和 coordsB 表示起点和终点所在的坐标系，这里分别为小饼图和大饼图的坐标系。

• axesA 和 axesB 分别表示起点和终点所在的子图对象，这里分别为小饼图和大饼图的子图对象，即 ax2 和 ax1。

3.5 连接线2，连接大饼图的下边缘和小饼图的饼块

x = r * np.cos(np.pi / 180 * theta1) + center[0]
y = np.sin(np.pi / 180 * theta1) + center[1]
con2 = ConnectionPatch(xyA=(-0.1, -0.49),
                       xyB=(x, y),
                       coordsA='data',
                       coordsB='data',
                       axesA=ax2, axesB=ax1)

这段代码用于创建连接线的第二个对象con2。具体解释如下：

• x 和 y 分别代表了连接线从小饼图中(-0.1,-0.49)这个点出发，到大饼图中theta1角度对应的点的终点坐标。其中，theta1是通过访问ax1.patches[-1].theta1获得的。

• coordsA 和 coordsB 表示终点和起点坐标的坐标系类型。这里都是 ‘data’ 表示使用数据坐标系，即默认的 x 和 y 坐标值。

• axesA 和 axesB 表示终点和起点所在的子图对象。其中，axesA 为小饼图，axesB 为大饼图。

• 这里使用ConnectionPatch函数创建连接线对象。

3.6 添加连接线

for con in [con1, con2]:
    con.set_color('gray')
    ax2.add_artist(con)
    con.set_linewidth(1)

这段代码用于设置连接线的颜色和粗细，并将连接线添加到小饼图的坐标系上。具体来说，循环遍历连接线对象列表 [con1, con2]，并依次对每个连接线进行以下操作：

• 调用 set_color() 方法设置连接线的颜色为灰色。

• 调用 ax2.add_artist() 方法将连接线添加到小饼图的坐标系上。

• 调用 set_linewidth() 方法设置连接线的宽度为 1。

3.7 调整子图布局

fig.subplots_adjust(wspace=0)
plt.show()

这行代码调整了子图之间的水平间距，将间距设置为0，即将子图紧密排列。wspace参数表示子图之间的宽度间距。具体来说，这行代码将第一个子图和第二个子图之间的间距设置为0，使它们之间没有空隙。

四、源代码

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import ConnectionPatch
from matplotlib import cm
# 大饼图数据
labels = ['301', '302', '303', '304', '305', '307', '308', '306']
size = [219324, 94739, 75146, 71831, 54051, 21458, 9990, 50843]
# 大饼图分裂距离
explode = (0, 0, 0, 0, 0, 0, 0, 0.1)
# 小饼图数据
labels2 = ['402', '407']
size2 = [12255, 207069]
width = 0.2
# 创建画布和子图对象
fig = plt.figure(figsize=(9, 5))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
# 绘制大饼图
ax1.pie(size,
        autopct='%1.1f%%',
        startangle=30,
        labels=labels,
        colors=cm.Blues(range(10, 300, 50)),
        explode=explode)
# 绘制小饼图
ax2.pie(size2,
        autopct='%1.1f%%',
        startangle=90,
        labels=labels2,
        colors=cm.Blues(range(10, 300, 50)),
        radius=0.5,
        shadow=False)
# 连接线1，连接大饼图的上边缘和小饼图的饼块
theta1, theta2 = ax1.patches[-1].theta1, ax1.patches[-1].theta2
center, r = ax1.patches[-1].center, ax1.patches[-1].r
x = r * np.cos(np.pi / 180 * theta2) + center[0]
y = np.sin(np.pi / 180 * theta2) + center[1]
con1 = ConnectionPatch(xyA=(0, 0.5),
                       xyB=(x, y),
                       coordsA=ax2.transData,
                       coordsB=ax1.transData,
                       axesA=ax2, axesB=ax1)
# 连接线2，连接大饼图的下边缘和小饼图的饼块
x = r * np.cos(np.pi / 180 * theta1) + center[0]
y = np.sin(np.pi / 180 * theta1) + center[1]
con2 = ConnectionPatch(xyA=(-0.1, -0.49),
                       xyB=(x, y),
                       coordsA='data',
                       coordsB='data',
                       axesA=ax2, axesB=ax1)
# 添加连接线
for con in [con1, con2]:
    con.set_color('gray')
    ax2.add_artist(con)
    con.set_linewidth(1)
# 调整子图布局
fig.subplots_adjust(wspace=0)
# 显示图像
plt.show()

可视化结果为：

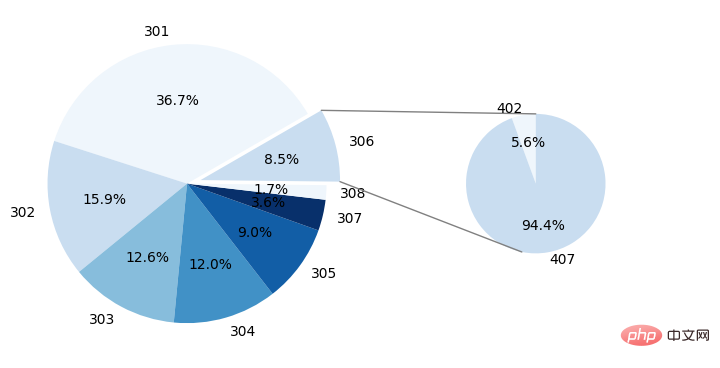
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!