Comment utiliser NumPy dans les fonctions courantes de Python-Tutoriel Python-php.cn

1.fichier txt

(1) La matrice d'identité

est une matrice carrée dans laquelle les éléments de la diagonale principale sont tous 1 et les éléments restants sont 0.

Dans NumPy, vous pouvez utiliser la fonction eye pour créer un tel tableau bidimensionnel. Il suffit de donner un paramètre pour spécifier le nombre de 1 éléments dans la matrice.

Par exemple, créez un tableau de 3×3 :

import numpy as np
I2 = np.eye(3)
print(I2)
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

Copier après la connexion

(2) Utilisez la fonction savetxt pour stocker les données dans un fichier. Bien sûr, nous devons spécifier le nom du fichier et le tableau à enregistrer.

np.savetxt(&#39;eye.txt&#39;, I2)#创建一个eye.txt文件，用于保存I2的数据

Copier après la connexion

2. Fichier CSV

Le format CSV (valeurs séparées par des virgules) est un format de fichier courant ; généralement, le fichier de vidage de la base de données est au format CSV et chaque champ du fichier correspond à une colonne dans une table de base de données ; Les logiciels de feuille de calcul (tels que Microsoft Excel) peuvent traiter les fichiers CSV.

note : , la fonction loadtxt de NumPy peut facilement lire les fichiers CSV, segmenter automatiquement les champs et charger des données dans des tableaux NumPy

contenu des données data.csv :

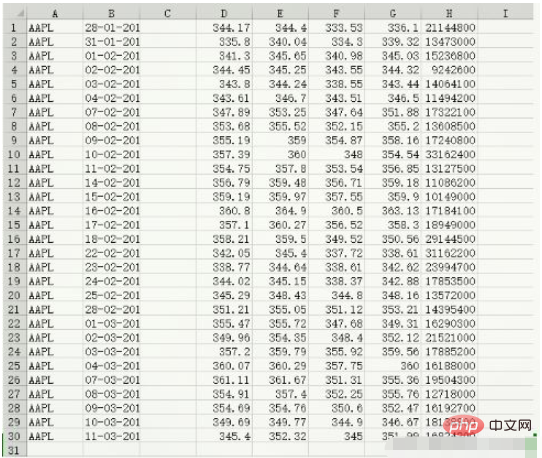
Comment utiliser NumPy dans les fonctions courantes de Python

c, v = np.loadtxt(&#39;data.csv&#39;, delimiter=&#39;,&#39;, usecols=(6,7), unpack=True)
# usecols的参数为一个元组，以获取第7字段至第8字段的数据
# unpack参数设置为True，意思是分拆存储不同列的数据，即分别将收盘价和成交量的数组赋值给变量c和v
print(c)
[336.1  339.32 345.03 344.32 343.44 346.5  351.88 355.2  358.16 354.54
 356.85 359.18 359.9  363.13 358.3  350.56 338.61 342.62 342.88 348.16
 353.21 349.31 352.12 359.56 360.   355.36 355.76 352.47 346.67 351.99]
print(v)
[21144800. 13473000. 15236800.  9242600. 14064100. 11494200. 17322100.
 13608500. 17240800. 33162400. 13127500. 11086200. 10149000. 17184100.
 18949000. 29144500. 31162200. 23994700. 17853500. 13572000. 14395400.
 16290300. 21521000. 17885200. 16188000. 19504300. 12718000. 16192700.
 18138800. 16824200.]
print(type(c))
print(type(v))
<class &#39;numpy.ndarray&#39;>
<class &#39;numpy.ndarray&#39;>

Copier après la connexion

3. Prix moyen pondéré en fonction du volume = fonction moyenne()

VWAP Présentation : Le VWAP (Volume-Weighted Average Price) est une grandeur économique très importante, qui représente le prix « moyen » des actifs financiers.

Plus le volume d'un certain prix est élevé, plus le poids de ce prix est important.

VWAP est une moyenne pondérée calculée avec le volume des transactions comme poids et est souvent utilisée dans le trading algorithmique.

vwap = np.average(c,weights=v)
print(&#39;成交量加权平均价格vwap =&#39;, vwap)
成交量加权平均价格vwap = 350.5895493532009

Copier après la connexion

4. Fonction moyenne arithmétique = fonction moyenne()

La fonction moyenne dans NumPy peut calculer la moyenne arithmétique des éléments du tableau

print(&#39;c数组中元素的算数平均值为： {}&#39;.format(np.mean(c)))
c数组中元素的算数平均值为： 351.0376666666667

Copier après la connexion

5. Prix moyen pondéré dans le temps

Aperçu TWAP :

In. En économie, le TWAP (Time-Weighted Average Price) est un autre indicateur des prix « moyens ». Maintenant que nous avons calculé le VWAP, calculons également le TWAP. En fait, le TWAP n’est qu’une variante. L’idée de base est que le prix récent est plus important, nous devrions donc lui accorder un poids plus élevé. La méthode la plus simple consiste à utiliser la fonction arange pour créer une séquence de nombres naturels qui commence à 0 et augmente séquentiellement. Le nombre de nombres naturels est le nombre de cours de clôture. Bien entendu, ce n’est pas nécessairement la bonne façon de calculer le TWAP.

t = np.arange(len(c))
print(&#39;时间加权平均价格twap=&#39;, np.average(c, weights=t))
时间加权平均价格twap= 352.4283218390804

Copier après la connexion

6. Valeurs maximales et minimales

h, l = np.loadtxt(&#39;data.csv&#39;, delimiter=&#39;,&#39;, usecols=(4,5), unpack=True)
print(&#39;h数据为： \n{}&#39;.format(h))
print(&#39;-&#39;*10)
print(&#39;l数据为： \n{}&#39;.format(l))
h数据为： 
[344.4  340.04 345.65 345.25 344.24 346.7  353.25 355.52 359.   360.
 357.8  359.48 359.97 364.9  360.27 359.5  345.4  344.64 345.15 348.43
 355.05 355.72 354.35 359.79 360.29 361.67 357.4  354.76 349.77 352.32]
----------
l数据为： 
[333.53 334.3  340.98 343.55 338.55 343.51 347.64 352.15 354.87 348.
 353.54 356.71 357.55 360.5  356.52 349.52 337.72 338.61 338.37 344.8
 351.12 347.68 348.4  355.92 357.75 351.31 352.25 350.6  344.9  345.  ]
print(&#39;h数据的最大值为： {}&#39;.format(np.max(h)))
print(&#39;l数据的最小值为： {}&#39;.format(np.min(l)))
h数据的最大值为： 364.9
l数据的最小值为： 333.53
NumPy中有一个ptp函数可以计算数组的取值范围
该函数返回的是数组元素的最大值和最小值之间的差值
也就是说，返回值等于max(array) - min(array)
print(&#39;h数据的最大值-最小值的差值为： \n{}&#39;.format(np.ptp(h)))
print(&#39;l数据的最大值-最小值的差值为： \n{}&#39;.format(np.ptp(l)))
h数据的最大值-最小值的差值为： 
24.859999999999957
l数据的最大值-最小值的差值为： 
26.970000000000027

Copier après la connexion

7. Analyse statistique

Médiane : Nous pouvons utiliser certains seuils pour supprimer les valeurs aberrantes, mais il existe en fait une meilleure façon, c'est la médiane.

Organisez les valeurs des variables par ordre de taille pour former une séquence. Le nombre au milieu de la séquence est la médiane.

Par exemple, si nous avons 5 valeurs1, 2, 3, 4 et 5, alors la médiane est le nombre du milieu 3.

m = np.loadtxt(&#39;data.csv&#39;, delimiter=&#39;,&#39;, usecols=(6,), unpack=True)
print(&#39;m数据中的中位数为： {}&#39;.format(np.median(m)))
m数据中的中位数为： 352.055
# 数组排序后，查找中位数
sorted_m = np.msort(m)
print(&#39;m数据排序： \n{}&#39;.format(sorted_m))
N = len(c)
print(&#39;m数据中的中位数为： {}&#39;.format((sorted_m[N//2]+sorted_m[(N-1)//2])/2))
m数据排序： 
[336.1  338.61 339.32 342.62 342.88 343.44 344.32 345.03 346.5  346.67
 348.16 349.31 350.56 351.88 351.99 352.12 352.47 353.21 354.54 355.2
 355.36 355.76 356.85 358.16 358.3  359.18 359.56 359.9  360.   363.13]
m数据中的中位数为： 352.055
方差：
方差是指各个数据与所有数据算术平均数的离差平方和除以数据个数所得到的值。
print(&#39;variance =&#39;, np.var(m))
variance = 50.126517888888884
var_hand = np.mean((m-m.mean())**2)
print(&#39;var =&#39;, var_hand)
var = 50.126517888888884

Copier après la connexion

Remarque : La différence de calcul entre la variance de l'échantillon et la variance de la population. La variance de la population est la somme des carrés des écarts divisée par le nombre de données, tandis que la variance de l'échantillon est la somme des carrés des écarts divisée par le nombre de données de l'échantillon moins 1, où le nombre de données de l'échantillon moins 1 (c'est-à-dire n- 1) est appelé degré de liberté. La raison de cette différence est de garantir que la variance de l'échantillon est un estimateur impartial.

8. Rendement des actions

Dans la littérature académique, l'analyse des cours de clôture est souvent basée sur les rendements boursiers et les rendements logarithmiques.

Le taux de rendement simple fait référence au taux de variation entre deux prix adjacents, tandis que le taux de rendement logarithmique fait référence à la différence entre les deux après avoir pris le logarithme de tous les prix.
Nous avons appris les logarithmes au lycée. Le logarithme de "a" moins le logarithme de "b" est égal au logarithme de "a divisé par b". Par conséquent, le rendement logarithmique peut également être utilisé pour mesurer le taux de variation du prix.

Notez que puisque le taux de rendement est un ratio, par exemple on divise le dollar américain par le dollar américain (il peut aussi s'agir d'autres unités monétaires), il est sans dimension.

En bref, ce qui intéresse le plus les investisseurs, c'est la variance ou l'écart type des rendements, car ils représentent l'ampleur du risque d'investissement.

(1) Tout d’abord, calculons le taux de rendement simple. La fonction diff de NumPy peut renvoyer un tableau constitué de la différence entre les éléments du tableau adjacents. C'est un peu similaire au calcul différentiel. Pour calculer le rendement, nous devons également diviser le prix de la veille par la différence. Cependant, veuillez noter ici que le tableau renvoyé par diff contient un élément de moins que le tableau des prix de clôture. return = np.diff(arr)/arr[:-1]

Notez que nous n'utilisons pas la dernière valeur du tableau des prix de clôture comme diviseur. Ensuite, utilisez la fonction std pour calculer l'écart type :

print ("Standard deviation =", np.std(returns))

Copier après la connexion

(2) Le retour du journal est encore plus simple à calculer. Nous utilisons d'abord la fonction log pour obtenir le logarithme de chaque cours de clôture, puis utilisons la fonction diff sur le résultat.

logreturns = np.diff( np.log(c) )

Copier après la connexion

Généralement, nous devons vérifier le tableau d'entrée pour nous assurer qu'il ne contient pas de zéros ni de nombres négatifs. Sinon, vous recevrez un message d'erreur. Cependant, dans notre exemple, le cours de l’action est toujours positif, le contrôle peut donc être omis.

(3) Nous serons probablement très intéressés par les jours de bourse qui génèrent des rendements positifs.

Après avoir terminé les étapes précédentes, il suffit d'utiliser la fonction Where pour ce faire. La fonction Where peut renvoyer les valeurs d'index de tous les éléments du tableau qui remplissent les conditions selon les conditions spécifiées.

Entrez le code suivant :

posretindices = np.where(returns > 0)
print "Indices with positive returns", posretindices
即可输出该数组中所有正值元素的索引。
Indices with positive returns (array([ 0, 1, 4, 5, 6, 7, 9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23, 25, 28]),)

Copier après la connexion

(4) 在投资学中，波动率（volatility）是对价格变动的一种度量。历史波动率可以根据历史价格数据计算得出。计算历史波动率（如年波动率或月波动率）时，需要用到对数收益率。年波动率等于对数收益率的标准差除以其均值，再除以交易日倒数的平方根，通常交易日取252天。用std和mean函数来计算

代码如下所示：

annual_volatility = np.std(logreturns)/np.mean(logreturns)
annual_volatility = annual_volatility / np.sqrt(1./252.)

Copier après la connexion

(5) sqrt函数中的除法运算。在Python中，整数的除法和浮点数的除法运算机制不同(python3已修改该功能)，我们必须使用浮点数才能得到正确的结果。与计算年波动率的方法类似，计算月波动率如下：

annual_volatility * np.sqrt(1./12.)

c = np.loadtxt(&#39;data.csv&#39;, delimiter=&#39;,&#39;, usecols=(6,), unpack=True)

returns = np.diff(c)/c[:-1]
print(&#39;returns的标准差： {}&#39;.format(np.std(returns)))
logreturns = np.diff(np.log(c))
posretindices = np.where(returns>0)
print(&#39;retruns中元素为正数的位置： \n{}&#39;.format(posretindices))
annual_volatility = np.std(logreturns)/np.mean(logreturns)
annual_volatility = annual_volatility/np.sqrt(1/252)
print(&#39;每年波动率: {}&#39;.format(annual_volatility))
print(&#39;每月波动率：{}&#39;.format(annual_volatility*np.sqrt(1/12)))
returns的标准差： 0.012922134436826306
retruns中元素为正数的位置： 
(array([ 0,  1,  4,  5,  6,  7,  9, 10, 11, 12, 16, 17, 18, 19, 21, 22, 23,
       25, 28], dtype=int64),)
每年波动率: 129.27478991115132
每月波动率：37.318417377317765

Copier après la connexion

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!