L'IA est à nouveau impliquée dans le monde des mathématiques et les nouvelles méthodes DSP doublent le taux de réussite des preuves automatiques

Démontrer automatiquement des théorèmes mathématiques est une intention originale de l'intelligence artificielle et a toujours été un problème. Jusqu'à présent, les mathématiciens humains ont utilisé deux manières différentes d'écrire les mathématiques.

La première méthode est une méthode que tout le monde connaît, qui consiste à utiliser le langage naturel pour décrire des preuves mathématiques. La plupart des mathématiques sont écrites de cette manière, y compris les manuels de mathématiques, les devoirs de mathématiques, etc.

Le deuxième type est appelé mathématiques formelles. Il s'agit d'un outil créé par des informaticiens au cours du dernier demi-siècle pour vérifier les preuves mathématiques.

De nos jours, il semble que les ordinateurs puissent être utilisés pour vérifier des preuves mathématiques, mais ils ne peuvent le faire qu'en utilisant des langages de preuve spécialement conçus qui ne peuvent pas gérer le mélange de notation mathématique et de texte écrit utilisé par les mathématiciens. La conversion de problèmes mathématiques écrits en langage naturel en code formel afin que les ordinateurs puissent les résoudre plus facilement peut aider à construire des machines capables d'explorer de nouvelles découvertes en mathématiques. Ce processus est appelé formalisation, et l'autoformalisation fait référence à la tâche de traduire automatiquement les mathématiques du langage naturel vers un langage formel.

L'automatisation des preuves formelles est une tâche difficile, et les méthodes d'apprentissage profond n'ont pas encore obtenu un grand succès dans ce domaine, principalement en raison de la rareté des données formelles. En fait, la preuve formelle elle-même est très difficile et seuls quelques experts peuvent la faire, ce qui rend irréalistes les efforts d’annotation à grande échelle. Le plus grand corpus de preuves formelles est écrit en code Isabelle (Paulson, 1994) et fait moins de 0,6 Go, soit des ordres de grandeur inférieurs aux ensembles de données couramment utilisés en vision ou en traitement du langage naturel. Pour remédier à la rareté des preuves formelles, des études antérieures ont proposé d'utiliser des données synthétiques, un apprentissage auto-supervisé ou par renforcement pour synthétiser des données de formation formelles supplémentaires. Bien que ces méthodes atténuent dans une certaine mesure le manque de données, elles ne sont pas en mesure d’exploiter pleinement le grand nombre de preuves mathématiques écrites manuellement.

Prenons comme exemple le modèle de langage Minerva. Après un entraînement avec suffisamment de données, nous avons constaté que ses capacités en mathématiques sont très fortes et qu'il peut obtenir des scores supérieurs à la moyenne aux tests de mathématiques du secondaire. Cependant, un tel modèle de langage présente également des inconvénients. Il ne peut qu’imiter, mais ne peut pas s’entraîner de manière indépendante pour améliorer les mathématiques. Les systèmes de preuve formelle fournissent un environnement de formation, mais il existe très peu de données pour les mathématiques formelles.

Contrairement aux mathématiques formelles, les données mathématiques informelles sont abondantes et largement disponibles. Récemment, de grands modèles de langage formés à partir de données mathématiques informelles ont démontré des capacités de raisonnement quantitatif impressionnantes. Cependant, ils produisent souvent des preuves erronées, et il est difficile de détecter automatiquement un raisonnement erroné dans ces preuves.

Dans un travail récent, des chercheurs tels que Yuhuai Tony Wu de Google ont conçu une nouvelle méthode appelée DSP (Draft, Sketch, and Prove) pour transformer les preuves mathématiques informelles en preuves formelles, elle possède à la fois la rigueur logique fournie par les preuves formelles systèmes et une grande quantité de données informelles.

Lien papier : https://arxiv.org/pdf/2210.12283.pdf

Plus tôt cette année, Wu Yuhuai et plusieurs collaborateurs ont utilisé le réseau neuronal d'OpenAI Codex Effectuer des opérations automatiques travail de formalisation et prouver la faisabilité de l'utilisation de grands modèles de langage pour traduire automatiquement des déclarations informelles en déclarations formelles. DSP va encore plus loin en utilisant de grands modèles de langage pour générer des croquis de preuves formelles à partir de preuves informelles. Les esquisses de preuve consistent en des étapes de raisonnement de haut niveau qui peuvent être interprétées par un système formel comme un prouveur de théorème interactif. Elles diffèrent des preuves formelles complètes en ce qu'elles contiennent des séquences de conjectures intermédiaires injustifiées. Dans la dernière étape du DSP, l'esquisse de la preuve formelle est élaborée en une preuve formelle complète, en utilisant un vérificateur automatique pour prouver toutes les conjectures intermédiaires.

Wu Yuhuai a déclaré : Maintenant, nous montrons que LLM peut convertir les preuves informelles qu'il génère en preuves formelles vérifiées !

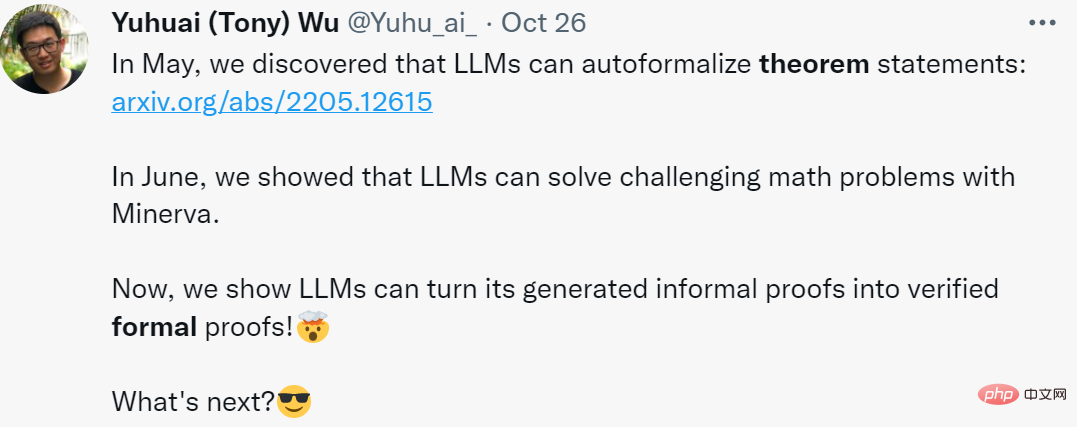
Méthodes

La section Méthodes décrit une approche DSP pour l'automatisation de la preuve formelle, qui utilise des preuves informelles pour guider les esquisses de preuves pour les prouveurs formels automatisés de théorèmes. On suppose ici que chaque problème a une proposition informelle et une proposition formelle décrivant le problème. Le pipeline global se compose de trois étapes (illustré dans la figure 1).

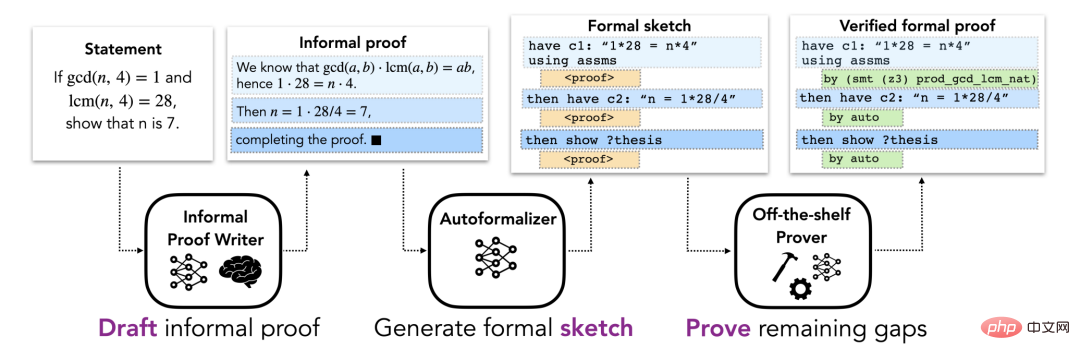
Figure 1.

Rédaction de la preuve informelle

L'étape initiale de la méthode DSP, comprenant la recherche d'une forme informelle du problème basée sur sa description en langage mathématique naturel (éventuellement en utilisant LATEX). La preuve informelle qui en résulte est traitée comme une ébauche pour les étapes ultérieures. Dans les manuels de mathématiques, des preuves de théorèmes sont généralement fournies, mais elles sont parfois manquantes ou incomplètes. Les chercheurs ont donc considéré deux situations correspondant à la présence ou à l’absence de preuves informelles.

Dans le premier cas, le chercheur suppose qu'il existe une « vraie » preuve informelle (c'est-à-dire une preuve écrite par un humain), ce qui est une situation typique dans la pratique formelle des théories mathématiques existantes. Dans le second cas, les chercheurs font l’hypothèse plus générale qu’aucune preuve informelle réelle n’est donnée et utilisent un grand modèle de langage formé sur des données mathématiques informelles pour rédiger des candidats à la preuve. Le modèle linguistique élimine la dépendance aux preuves humaines et peut générer plusieurs solutions alternatives à chaque problème. Bien qu'il n'existe pas de moyen simple de vérifier automatiquement l'exactitude de ces preuves, les preuves informelles ne doivent être utiles qu'à l'étape suivante, dans la génération d'une bonne esquisse de preuve formelle.

Mappez les preuves informelles en croquis formels

Les croquis de preuves formelles codent la structure d'une solution et laissent de côté les détails de bas niveau. Intuitivement, il s’agit d’une preuve partielle qui décrit un énoncé conjectural de haut niveau. La figure 2 est un exemple concret de croquis d’épreuve. Bien que les preuves informelles laissent souvent de côté les détails de bas niveau, ces détails ne peuvent pas être exclus dans les preuves formelles, ce qui rend difficile la conversion directe des preuves informelles en preuves formelles. Au lieu de cela, cet article propose de mapper des preuves informelles sur des esquisses de preuves formelles partageant la même structure de haut niveau. Les détails de bas niveau manquant dans le croquis de preuve peuvent être complétés par le prouveur automatique. Puisqu’il n’existe pas de grands corpus parallèles informels-formels, les méthodes de traduction automatique standard ne conviennent pas à cette tâche. Au lieu de cela, les capacités d'apprentissage en quelques étapes d'un grand modèle de langage sont utilisées ici. Plus précisément, quelques paires d'exemples contenant des preuves informelles et leurs esquisses formelles correspondantes sont utilisées pour inciter le modèle, suivi d'une preuve informelle à convertir, puis laisser le modèle générer des jetons ultérieurs pour obtenir l'esquisse formelle requise. Ce modèle est appelé « formaliseur automatique ».

Figure 2. Conjecture ouverte dans l'esquisse de preuve Un « prouveur automatique » fait ici référence à un système qui peut produire des preuves formellement vérifiables. Le cadre est indépendant du choix spécifique du prouveur automatique : il peut s'agir d'un prouveur symbolique (tel qu'un outil d'automatisation de la preuve heuristique), d'un prouveur basé sur un réseau neuronal ou d'une approche hybride. Si le prouveur automatique comble avec succès toutes les lacunes de l'esquisse de preuve, il renvoie une preuve formelle finale qui peut être vérifiée par rapport à la spécification du problème. Si le prouveur automatique échoue (par exemple s’il dépasse le temps imparti), l’évaluation est considérée comme un échec.

Expériences

Les chercheurs ont mené une série d'expériences, y compris des preuves formelles de problèmes générés à partir de l'ensemble de données miniF2F, et ont montré qu'une grande proportion de théorèmes peuvent être automatiquement prouvés à l'aide de cette méthode. Deux environnements sont étudiés ici, où les preuves informelles sont écrites par des humains ou rédigées par un grand modèle de langage formé sur des textes mathématiques. Ces deux contextes correspondent à des situations qui surviennent souvent dans la formalisation de théories existantes, c'est-à-dire qu'il existe souvent des preuves informelles, mais elles sont parfois laissées en exercice au lecteur, ou manquent en raison de contraintes dans les marges.

Le tableau 1 montre la proportion de preuves formelles réussies trouvées sur l'ensemble de données miniF2F. Les résultats incluent quatre lignes de base issues de nos expériences, ainsi que la méthode DSP avec des preuves écrites par des humains et des preuves générées par des modèles.

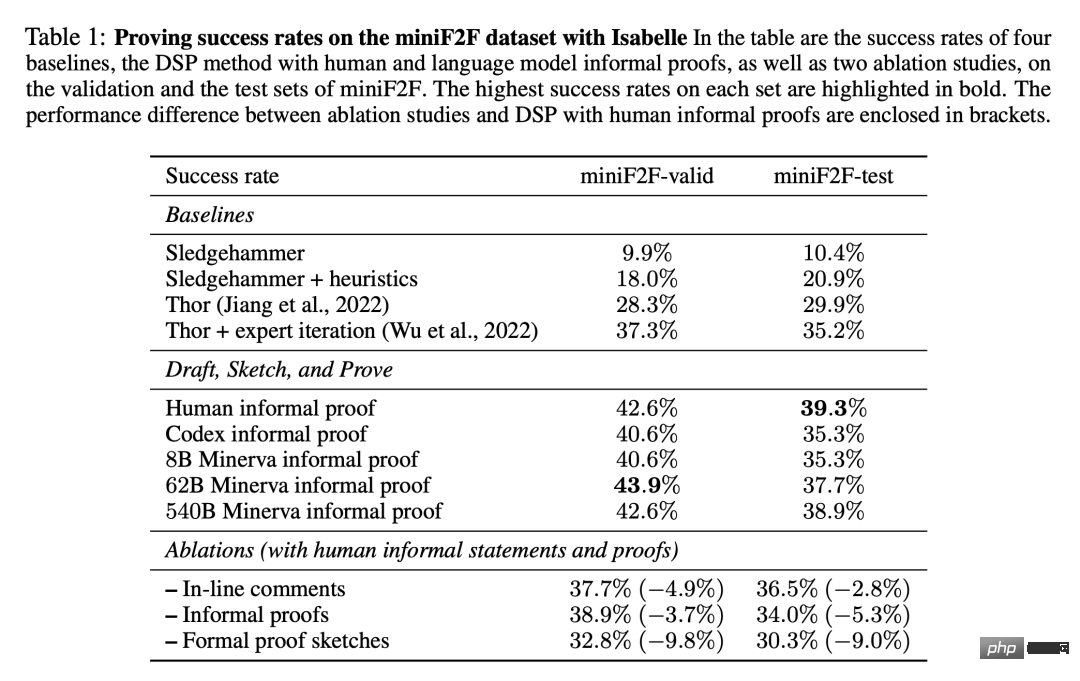
On peut voir que le prouveur automatique avec 11 stratégies heuristiques attachées augmente considérablement les performances de Sledgehammer, augmentant son taux de réussite de 9,9% à 18,0% sur l'ensemble de vérification de miniF2F sur l'ensemble de test. , il est passé de 10,4% à 20,9%. Deux références utilisant des modèles de langage et la recherche de preuves ont obtenu des taux de réussite de 29,9 % et 35,2 % respectivement sur l'ensemble de tests de miniF2F.

Basée sur des preuves informelles écrites par des humains, la méthode DSP atteint des taux de réussite de 42,6% et 39,3% sur les ensembles de validation et de test de miniF2F. Au total, 200 des 488 problèmes peuvent être prouvés de cette manière. Le modèle Codex et le modèle Minerva (8B) ont donné des résultats très similaires lors de la résolution de problèmes sur miniF2F : ils ont tous deux guidé le vérificateur automatique pour résoudre respectivement 40,6 % et 35,3 % des problèmes sur les ensembles de validation et de test.

Lors du passage au modèle Minerva (62B), les taux de réussite sont passés à 43,9% et 37,7% respectivement. Par rapport aux preuves informelles écrites par des humains, son taux de réussite est 1,3 % plus élevé sur l’ensemble de validation et 1,6 % inférieur sur l’ensemble de tests. Au total, le modèle Minerva (62B) a pu résoudre 199 problèmes sur miniF2F, soit un de moins qu'une preuve écrite par un humain. Le modèle Minerva (540B) a résolu respectivement 42,6 % et 38,9 % des problèmes dans l'ensemble de validation et l'ensemble de test de miniF2F, et a également généré 199 preuves réussies.

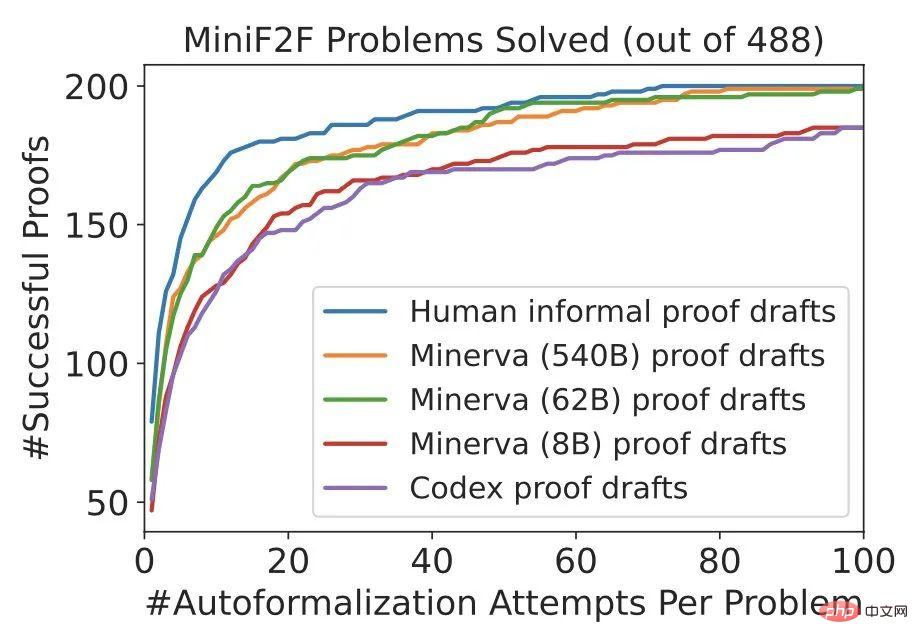
Les méthodes DSP guident efficacement les prouveurs automatiques dans les deux cas : preuves informelles utilisant des humains ou preuves informelles générées par des modèles de langage. DSP a presque doublé le taux de réussite du prouveur et a produit des performances SOTA sur miniF2F en utilisant Isabelle. De plus, les modèles Minerva plus grands sont presque aussi utiles que les humains pour guider les prouveurs formels automatisés.

Comme le montre la figure ci-dessous, la méthode DSP améliore considérablement les performances du prouveur heuristique Sledgehammer + (~20% -> ~40%), en obtenant un nouveau SOTA sur miniF2F.

Les versions 62B et 540B de Minerva génèrent des preuves très similaires aux preuves humaines.

Pour plus d'informations, veuillez vous référer au document original.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!