
La liste de contiguïté est une méthode de stockage en chaîne pour les graphiques. Sa structure de données se compose de deux parties : les nœuds et les points adjacents.
Les listes de contiguïté peuvent être utilisées pour représenter des graphiques non orientés, des graphiques orientés et des réseaux. Ceci est expliqué à l’aide d’un graphe non orienté.
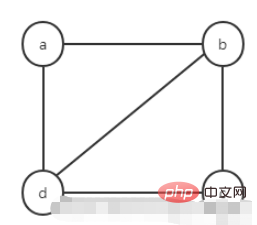
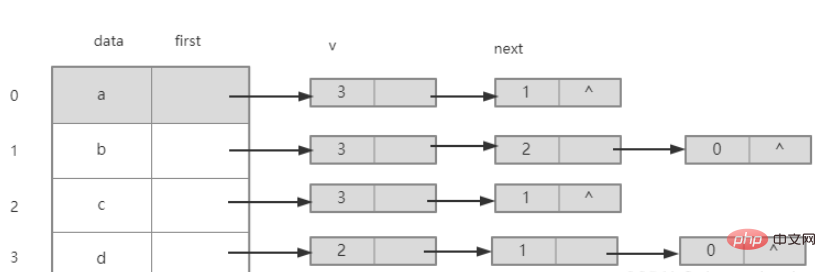
Les points adjacents du nœud b sont les nœuds a, c et d. Les index de stockage de leurs points adjacents sont 0, 2 et 3. Ils sont placés dans la liste chaînée derrière le nœud b selon la méthode d'insertion de tête ( ordre inverse).
Les points adjacents du nœud c sont les nœuds b et d, et les index de stockage de leurs points adjacents sont 1 et 3. Ils sont placés dans la liste chaînée derrière le nœud c selon la méthode d'interpolation de tête (ordre inverse).
Les points adjacents du nœud d sont les nœuds a, b et c. Les index de stockage de leurs points adjacents sont 0, 1 et 2. Ils sont placés dans la liste chaînée derrière le nœud d selon la méthode d'insertion de tête ( ordre inverse).
4. Les caractéristiques de la liste de contiguïté du graphe non orienté
Le degré d'un nœud est le nombre de nœuds dans la liste à chaînage unique derrière le nœud.
2. Structure de données de la liste de contiguïté
 2. Le point adjacent
2. Le point adjacent
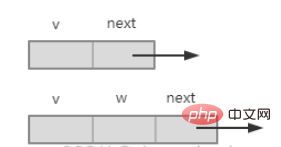 3. Étapes de l'algorithme
3. Étapes de l'algorithme
2 Entrez tour à tour les informations du nœud, stockez-les dans le champ de données du tableau de nœuds Vex[] et laissez le premier champ Vex[] vide.
3 Saisissez tour à tour les deux nœuds attachés à chaque bord. S'il s'agit d'un réseau, vous devez également saisir le poids du bord.
S'il s'agit d'un graphe non orienté, entrez a b, interrogez les nœuds a, b, stockez les indices i, j dans le tableau de nœuds Vex[], créez un nouveau point adjacent s, soit s.v = j;s.next=null ; Insérez ensuite le nœud s avant le premier point adjacent du i-ème nœud (méthode d'interpolation de tête). Dans un graphe non orienté, il y a une arête du nœud a au nœud b, et il y a une arête du nœud b au nœud a, donc un nouveau point de contiguïté s2 doit être créé, soit s2.v = i;s2.next= null; puis let Le nœud s2 est inséré avant le premier point adjacent du j-ème nœud (méthode d'interpolation de tête).
S'il s'agit d'un graphe non orienté, entrez a b, interrogez les nœuds a, b, stockez les indices i, j dans le tableau de nœuds Vex[], créez un nouveau point adjacent s, soit s.v = j;s.next=null ; Insérez ensuite le nœud s avant le premier point adjacent du i-ème nœud (méthode d'interpolation de tête).
S'il s'agit d'un réseau non orienté ou d'un réseau orienté, il est traité de la même manière qu'un graphe non orienté ou un graphe orienté, sauf que les nœuds voisins ont un domaine de poids supplémentaire.
4. Mise en œuvre
package graph;
import java.util.Scanner;
public class CreateALGraph {
static final int MaxVnum = 100; // 顶点数最大值
public static void main(String[] args) {
ALGraph G = new ALGraph();
for (int i = 0; i < G.Vex.length; i++) {
G.Vex[i] = new VexNode();
}
CreateALGraph(G); // 创建有向图邻接表
printg(G); // 输出邻接表
}
static int locatevex(ALGraph G, char x) {
for (int i = 0; i < G.vexnum; i++) // 查找顶点信息的下标
if (x == G.Vex[i].data)
return i;
return -1; // 没找到
}
// 插入一条边
static void insertedge(ALGraph G, int i, int j) {
AdjNode s = new AdjNode();
s.v = j;
s.next = G.Vex[i].first;
G.Vex[i].first = s;
}
// 输出邻接表
static void printg(ALGraph G) {
System.out.println("----------邻接表如下:----------");
for (int i = 0; i < G.vexnum; i++) {
AdjNode t = G.Vex[i].first;
System.out.print(G.Vex[i].data + ": ");
while (t != null) {
System.out.print("[" + t.v + "]\t");
t = t.next;
}
System.out.println();
}
}
// 创建有向图邻接表
static void CreateALGraph(ALGraph G) {
int i, j;
char u, v;
System.out.println("请输入顶点数和边数:");
Scanner scanner = new Scanner(System.in);
G.vexnum = scanner.nextInt();
G.edgenum = scanner.nextInt();
System.out.println("请输入顶点信息:");
for (i = 0; i < G.vexnum; i++)//输入顶点信息,存入顶点信息数组
G.Vex[i].data = scanner.next().charAt(0);
for (i = 0; i < G.vexnum; i++)
G.Vex[i].first = null;
System.out.println("请依次输入每条边的两个顶点u,v");
while (G.edgenum-- > 0) {
u = scanner.next().charAt(0);
v = scanner.next().charAt(0);
i = locatevex(G, u); // 查找顶点 u 的存储下标
j = locatevex(G, v); // 查找顶点 v 的存储下标
if (i != -1 && j != -1)
insertedge(G, i, j);
else {
System.out.println("输入顶点信息错!请重新输入!");
G.edgenum++; // 本次输入不算
}
}
}
}
// 定义邻接点类型
class AdjNode {
int v; // 邻接点下标
AdjNode next; // 指向下一个邻接点
}
// 定义顶点类型
class VexNode {
char data; // VexType为顶点的数据类型,根据需要定义
AdjNode first; // 指向第一个邻接点
}
// 定义邻接表类型
class ALGraph {
VexNode Vex[] = new VexNode[CreateALGraph.MaxVnum];
int vexnum; // 顶点数
int edgenum; // 边数
}Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!