
Le problème de la Tour de Hanoï est un problème classique. La tour de Hanoï, également connue sous le nom de tour de Hanoï, tire son origine d'une ancienne légende indienne. Lorsque Brahma a créé le monde, il a construit trois piliers de diamant. Sur un pilier, 64 disques d'or ont été empilés par ordre de taille, de bas en haut. Brahma a ordonné au brahmane de réorganiser les disques sur un autre pilier par ordre de taille à partir du bas. Il est également stipulé qu'à aucun moment, le disque ne peut être agrandi sur le petit disque, et qu'un seul disque peut être déplacé entre les trois piliers à la fois. Demandez comment fonctionner?
Ma propre compréhension est la suivante : continuez à réduire la taille de vos propres problèmes jusqu'à ce qu'ils soient réduits au point où ils ne peuvent plus être réduits. (La condition finale de la récursion est atteinte) Commencez ensuite à résoudre les petits problèmes. Après avoir résolu les petits problèmes un par un, le gros problème sera résolu (la récursion est de retour)
3. Le processus est le suivant :
4. La clé de la récursivité est :
(2) S'appeler constamment pour réduire la taille du problème et se rapprocher de la condition finale de la récursion.
Problème de la Tour de Hanoï
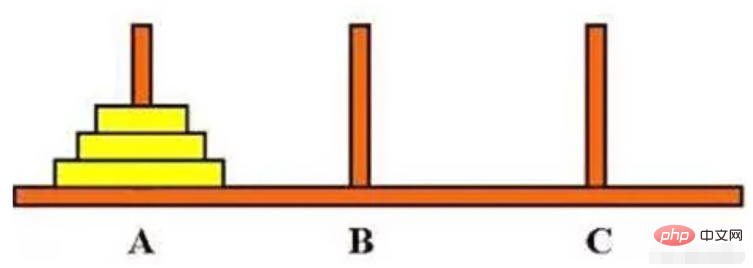 2. Processus récursif d'analyse des problèmes :
2. Processus récursif d'analyse des problèmes :
(2) Déplacez la plaque inférieure de A à C
(3 ) Déplacez les n-1 plaques supérieures de B à C à l'aide de A
La condition finale de la récursion :
L'échelle du problème devient lorsque le nombre de plaques est 0, car lorsque le nombre de plaques est 0 Pas besoin bouger! ! !
3. Code (Python)
# coding:utf-8
"""
n为初始时A柱上的盘子数
a为起始盘子所在的柱子
b为中转柱子
c为目的地柱子
"""
def hanoi(n, a, b, c):
if n > 0:
hanoi(n-1, a, c, b)
print("盘子从%s移动到%s" % (a, c))
hanoi(n-1, b, a, c)
hanoi(3, "A", "B", "C")Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!