Comment créer un tas de structures de données Java

Propriétés du tas

Le tas est logiquement un arbre binaire complet, et le tas est physiquement stocké dans un tableau.

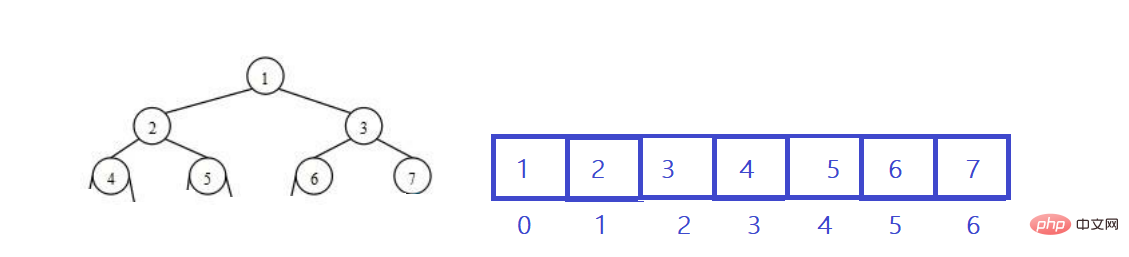
Résumé : Un arbre binaire complet est stocké dans un tableau à l'aide d'un parcours par ordre de niveau. L'utilisation principale de cette méthode est la représentation en tas.

Et si l'indice du parent est connu,

alors : indice enfant gauche (gauche) = 2 * parent + 1 ;

enfant droit (droite) indice = 2 * parent + 2 ;

Étant donné l'indice de l'enfant (sans distinguer gauche et droite), alors :

Parent (parent) indice = (enfant - 1) / 2;

Classification des tas

Grand tas : le nœud racine est plus grand que l'enfant gauche et droit nœuds Un arbre binaire complet (le nœud parent est plus grand que son nœud enfant) est appelé un gros tas, ou un gros tas racine, ou un tas maximum.

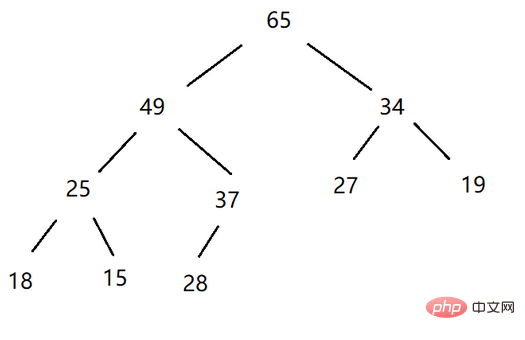
Petit tas : un arbre binaire complet dans lequel le nœud racine est plus petit que les nœuds enfants gauche et droit est appelé un petit tas (le nœud parent est plus petit que ses nœuds enfants), ou un petit tas racine, ou un tas minimum.

Ajustement vers le bas du tas

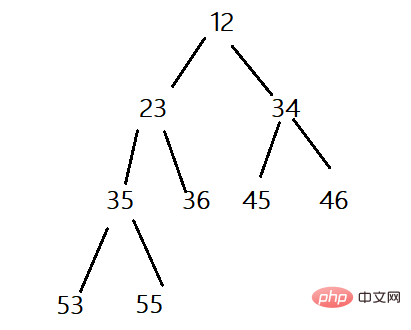
Il existe maintenant un tableau, qui est logiquement un arbre binaire complet, nous pouvons l'ajuster en un petit tas ou un grand tas grâce à l'algorithme d'ajustement vers le bas en partant du nœud racine. L'algorithme d'ajustement vers le bas a un principe : les sous-arbres gauche et droit doivent constituer un tas avant de pouvoir être ajustés.

Prenons un petit tas comme exemple :

1 Tout d'abord, laissez les nœuds enfants gauche et droit comparer et prendre la valeur minimale.

2. Comparez le plus petit nœud enfant avec le nœud parent. Si le nœud enfant

3. Le cycle continue. Si l'indice du nœud enfant est hors limites, cela signifie qu'il a atteint la fin et qu'il est terminé.

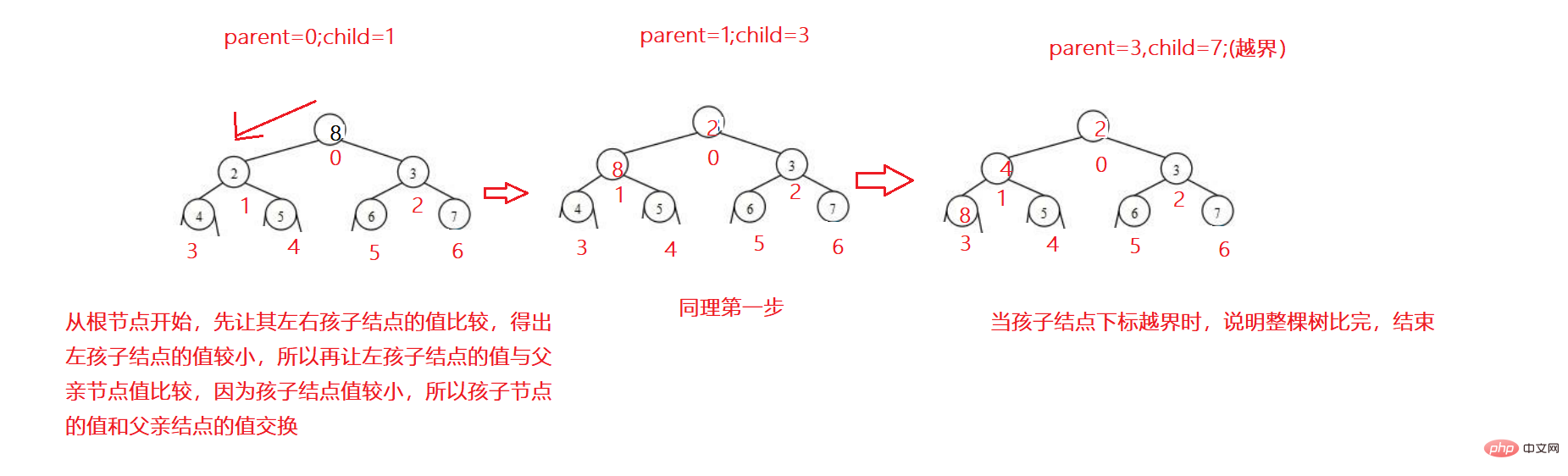
Exemple de code :

 //parent: 每棵树的根节点
 //len: 每棵树的调整的结束位置
public void shiftDown(int parent,int len){
        int child=parent*2+1; //因为堆是完全二叉树，没有左孩子就一定没有右孩子，所以最起码是有左孩子的，至少有1个孩子
        while(child<len){
            if(child+1<len && elem[child]<elem[child+1]){
                child++;//两孩子结点比较取较小值
            }
            if(elem[child]<elem[parent]){
                int tmp=elem[parent];
                elem[parent]=elem[child];
                elem[child]=tmp;
                parent=child;
                child=parent*2+1;
            }else{
                break;
            }
        }
    }

Construire un tas

Étant donné un tableau, ce tableau peut logiquement être considéré comme un arbre binaire complet, mais ce n'est pas encore un tas (les sous-arbres gauche et droit ne sont pas tous deux grands ou small) Heap), nous utilisons maintenant l'algorithme pour le construire en un tas (grand ou petit tas). Ce qu'il faut faire? Ici, nous commençons l'ajustement à partir du premier sous-arbre du dernier nœud non-feuille, et l'ajustons jusqu'à l'arbre du nœud racine, puis nous pouvons l'ajuster en une pile. Nous utiliserons ici l’ajustement à la baisse que nous venons d’écrire.

public void creatHeap(int[] arr){
        for(int i=0;i<arr.length;i++){
            elem[i]=arr[i];
            useSize++;
        }
        for(int parent=(useSize-1-1)/2;parent>=0;parent--){//数组下标从0开始
            shiftDown(parent,useSize);
        }
    }

La complexité spatiale de la construction d'un tas est O(N), car le tas est un arbre binaire complet, et un arbre binaire complet est également un arbre binaire complet (dans le pire des cas) pour. prouve-le.

Le tas doit être ajusté vers le haut

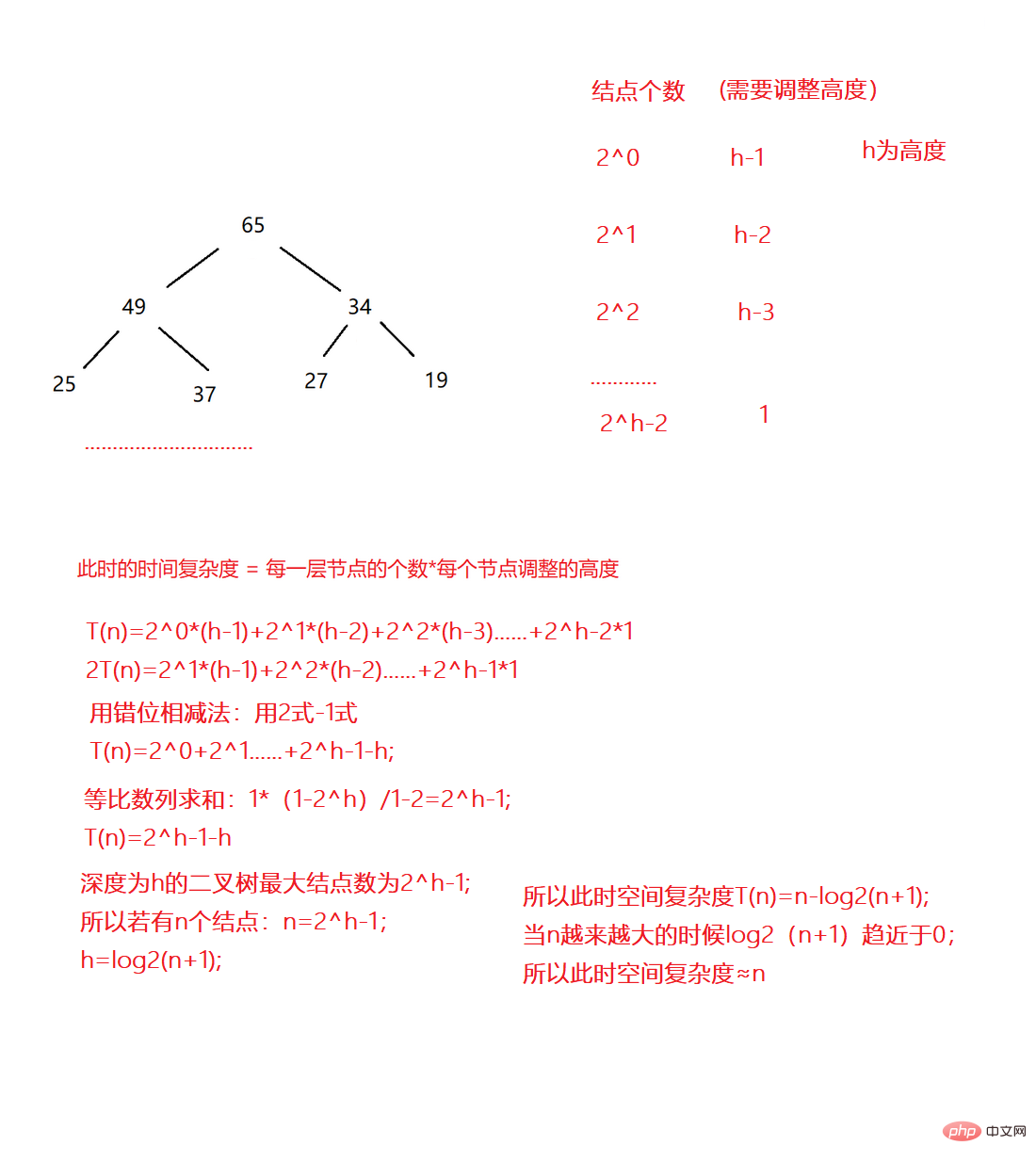
Maintenant, il y a un tas, nous devons insérer des données à la fin du tas, puis l'ajuster pour qu'il conserve toujours la structure du tas, c'est un ajustement vers le haut .

Prenons un grand tas comme exemple :

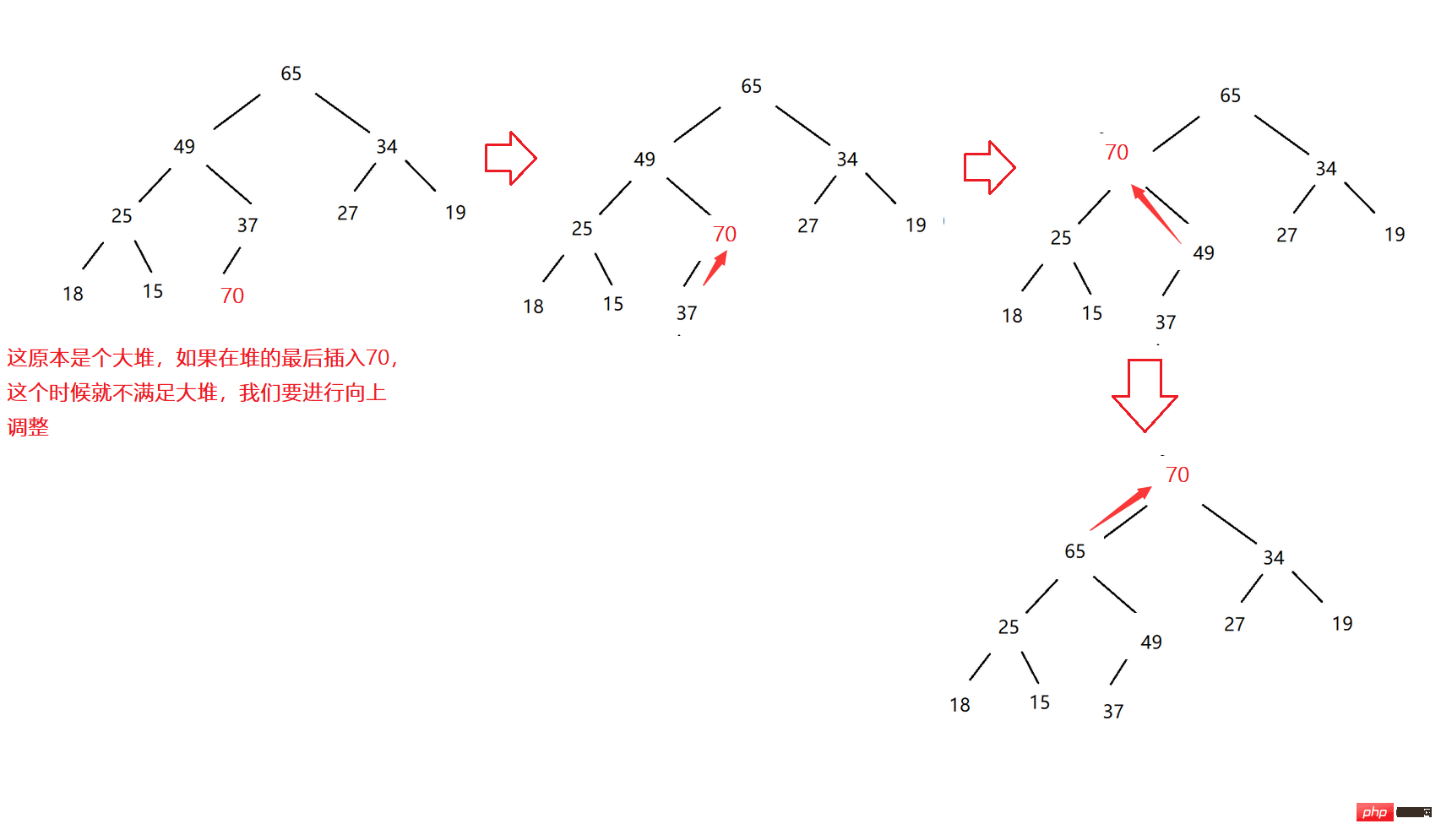
Exemple de code :

public void shiftup(int child){
        int parent=(child-1)/2;
        while(child>0){
            if(elem[child]>elem[parent]){
                int tmp=elem[parent];
                elem[parent]=elem[child];
                elem[child]=tmp;
                child=parent;
                parent=(child-1)/2;
            }else{
                break;
            }
        }
    }

Opérations courantes du tas

Mise en file d'attente

Pour ajouter un élément au tas, c'est-à-dire l'ajouter à la dernière position, et puis ajustez-le vers le haut.

public boolean isFull(){
        return elem.length==useSize;
    }
public void offer(int val){
        if(isFull()){
            elem= Arrays.copyOf(elem,2*elem.length);//扩容
        }
        elem[useSize++]=val;
        shiftup(useSize-1);
    }

Dequeue

Pour supprimer l'élément du tas, échangez l'élément supérieur du tas avec le dernier élément, puis diminuez la taille de l'ensemble du tableau d'un, et enfin ajustez-le vers le bas pour supprimer l'élément supérieur de la pile .

public boolean isEmpty(){
        return useSize==0;
    }
public int poll(){
        if(isEmpty()){
            throw new RuntimeException("优先级队列为空");
        }
        int tmp=elem[0];
        elem[0]=elem[useSize-1];
        elem[useSize-1]=tmp;
        useSize--;
        shiftDown(0,useSize);
        return tmp;
    }

Obtenez l'élément chef d'équipe

public int peek() {
        if (isEmpty()) {
            throw new RuntimeException("优先级队列为空");
        }
        return elem[0];
    }

Question TopK

Donnez-vous 6 données, trouvez les 3 plus grandes données. Comment utilisons-nous le tas à ce moment-là ?

Idées de résolution de problèmes :

1. Si vous souhaitez trouver les K premiers éléments les plus grands, vous devez créer un petit tas de racines.

2. Si vous souhaitez trouver les K premiers éléments les plus petits, vous devez construire un grand tas de racines.

3. Le Kème plus grand élément. Construisez un petit tas, et l'élément supérieur du tas est le Kième plus grand élément.

4. Le Kème plus petit élément. Construisez un gros tas, et l’élément supérieur du tas est le Kième plus grand élément.

Exemple

Par exemple : recherchez les n premières données les plus grandes

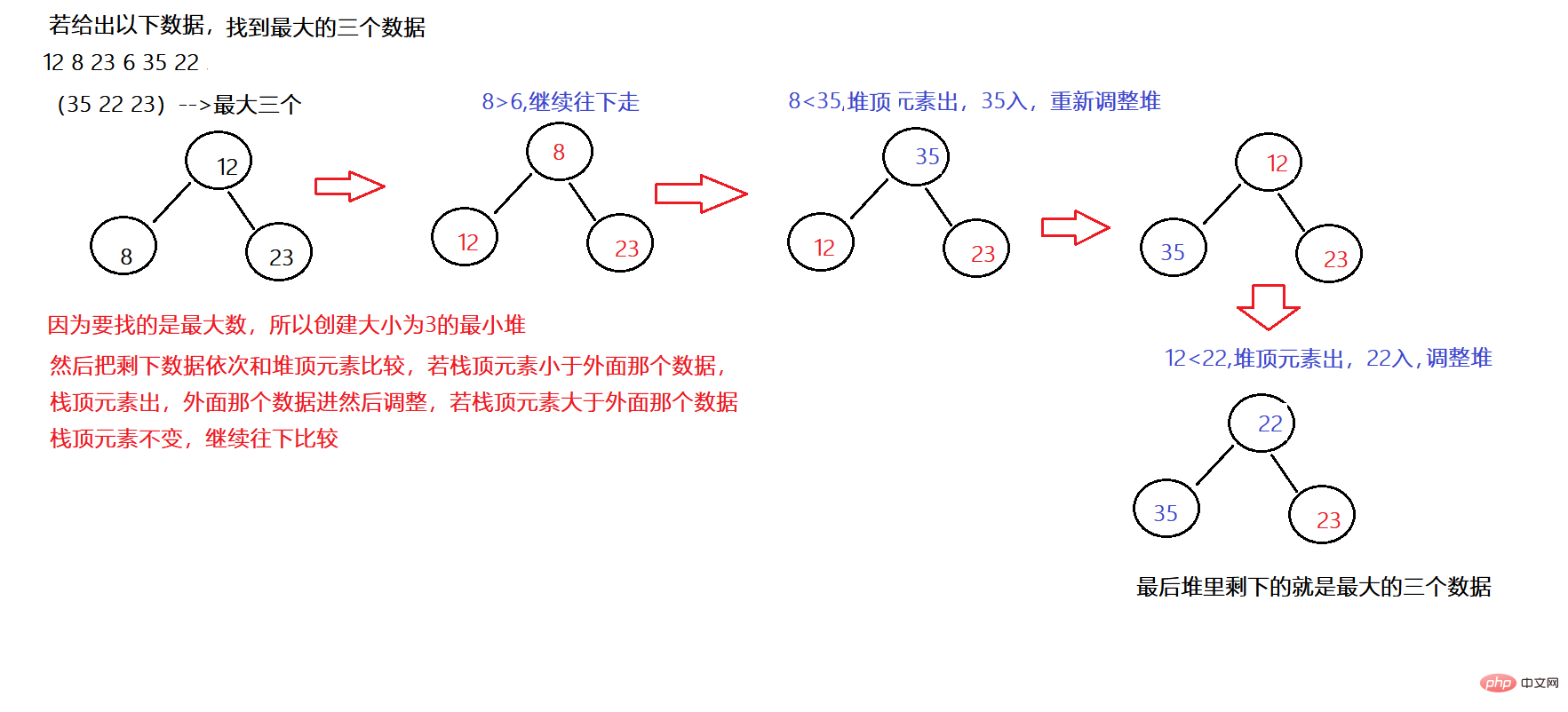
Exemple de code :

 public static int[] topK(int[] array,int k){
        //创建一个大小为K的小根堆
        PriorityQueue<Integer> minHeap=new PriorityQueue<>(k, new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1-o2;
            }
        });
        //遍历数组中元素，将前k个元素放入队列中
        for(int i=0;i<array.length;i++){
            if(minHeap.size()<k){
                minHeap.offer(array[i]);
            }else{
                //从k+1个元素开始，分别和堆顶元素比较
                int top=minHeap.peek();
                if(array[i]>top){
                    //先弹出后存入
                    minHeap.poll();
                    minHeap.offer(array[i]);
                }
            }
        }
        //将堆中元素放入数组中
        int[] tmp=new int[k];
        for(int i=0;i< tmp.length;i++){
            int top=minHeap.poll();
            tmp[i]=top;
        }
        return tmp;
    }
    public static void main(String[] args) {
        int[] array={12,8,23,6,35,22};
        int[] tmp=topK(array,3);
        System.out.println(Arrays.toString(tmp));
    }

Résultat :

Tri de tableau

De plus, si vous souhaitez trier un tableau du plus petit au plus grand, Faut-il utiliser de gros tas de racines ou des petits tas de racines ?

---->Dagendui

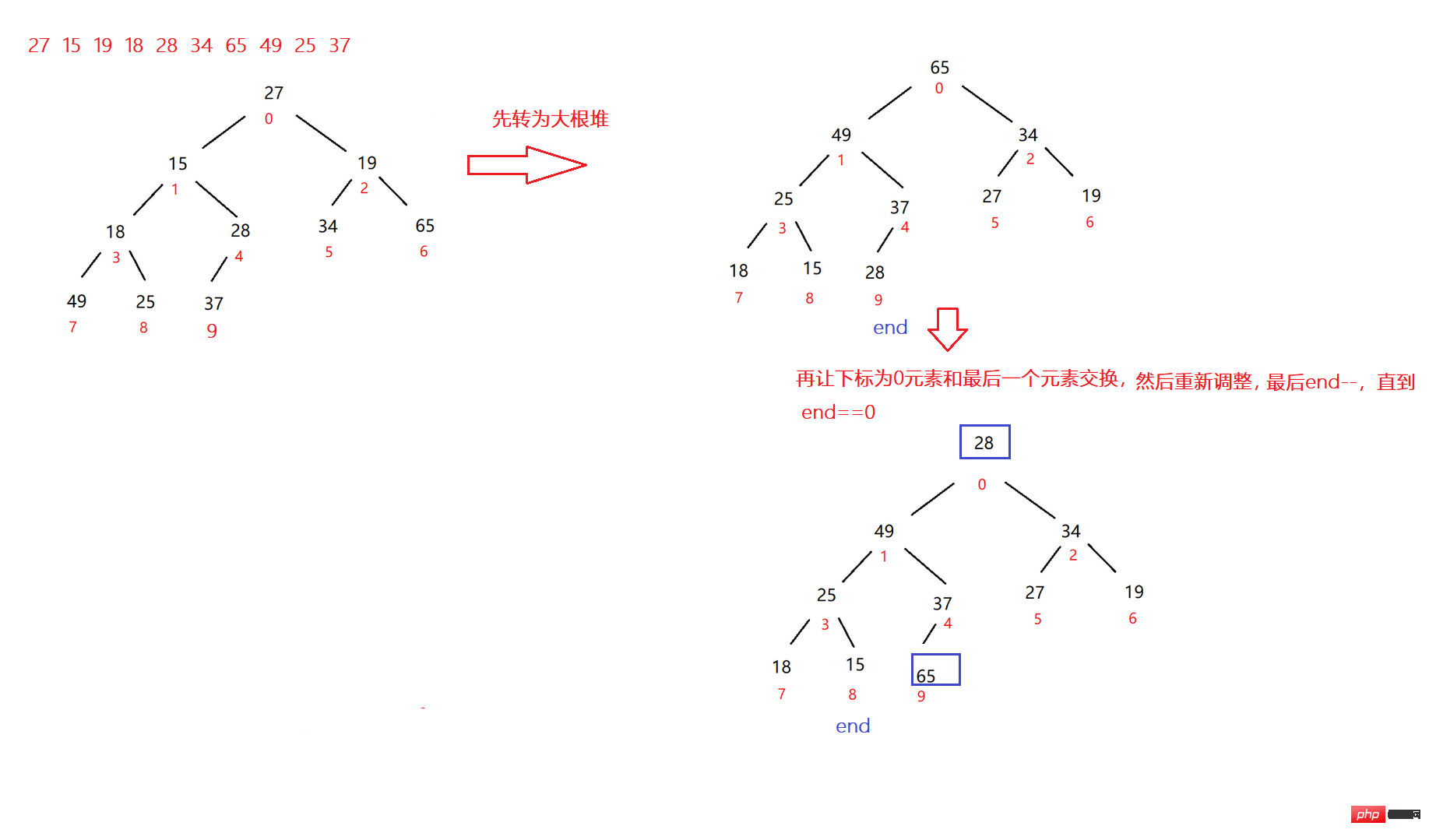
Exemple de code :

  public void heapSort(){
        int end=useSize-1;
        while(end>0){
            int tmp=elem[0];
            elem[0]=elem[end];
            elem[end]=tmp;
            shiftDown(0,end);//假设这里向下调整为大根堆
            end--;
        }
    }

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!