Un problème quantique qui nécessitait la résolution de 100 000 équations a été compressé par l'IA en seulement quatre sans sacrifier la précision.

Les électrons en interaction présentent une variété de phénomènes uniques à différentes énergies et températures. Si nous modifions leur environnement, ils auront de nouveaux comportements collectifs, tels que la rotation, les fluctuations d'appariement, etc. Cependant, lorsqu'il s'agit d'électrons, il existe encore de nombreuses difficultés. dans ces phénomènes. De nombreux chercheurs utilisent le Renormalization Group (RG) pour résoudre ce problème.

Dans le contexte des données de grande dimension, l'émergence de la technologie d'apprentissage automatique (ML) et des méthodes basées sur les données a suscité un grand intérêt parmi les chercheurs en physique quantique. Jusqu'à présent, les idées du ML ont été utilisées dans l'interaction de l'électronique. systèmes .

Dans cet article, des physiciens de l'Université de Bologne et d'autres institutions utilisent l'intelligence artificielle pour compresser un problème quantique qui a jusqu'à présent nécessité 100 000 équations en une petite tâche de seulement 4 équations, qui sont toutes complétées sans sacrifier la précision, la recherche a été récemment publiée dans Physical Review Letters.

Adresse papier : https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.136402

Domenico Di Sante, premier auteur de l'étude et professeur adjoint à la Université de Bologne, a déclaré : Nous avons couplé cet énorme projet et avons ensuite utilisé l'apprentissage automatique pour le condenser en tâches qui peuvent être comptées sur un seul doigt.

Cette étude porte sur la question de savoir comment les électrons se comportent lorsqu'ils se déplacent à travers un réseau en forme de grille. Selon l’expérience existante, lorsque deux électrons occupent le même réseau, ils interagissent. Ce phénomène, connu sous le nom de modèle Hubbard, est une configuration idéalisée de certains matériaux qui permet aux scientifiques de comprendre comment le comportement des électrons crée des phases de la matière, telles que la supraconductivité, dans lesquelles les électrons circulent à travers le matériau sans résistance. Le modèle peut également servir de terrain d’essai pour de nouvelles méthodes avant qu’elles ne soient appliquées à des systèmes quantiques plus complexes.

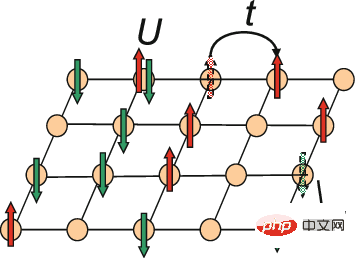
Schéma schématique du modèle bidimensionnel de Hubbard

Le modèle Hubbard semble simple, mais même l'utilisation de méthodes informatiques de pointe pour traiter un petit nombre d'électrons nécessite une puissance de calcul puissante. En effet, lorsque les électrons interagissent, ils s’entremêlent mécaniquement : même si les électrons sont éloignés l’un de l’autre dans le réseau, les deux électrons ne peuvent pas être traités indépendamment, les physiciens doivent donc les traiter tous simultanément, plutôt que de travailler avec un seul. électron à la fois. Plus il y a d’électrons, plus il y aura d’intrication mécanique quantique et la difficulté de calcul augmentera de façon exponentielle.

Une méthode courante pour étudier les systèmes quantiques est le groupe de renormalisation. En tant qu'appareil mathématique, les physiciens l'utilisent pour observer le comportement d'un système, comme le modèle Hubbard. Malheureusement, un groupe de renormalisation enregistre tous les couplages possibles entre électrons, qui peuvent contenir des milliers, des centaines de milliers, voire des millions d'équations indépendantes qui doivent être résolues. De plus, les équations sont complexes : chaque équation représente une paire d’électrons en interaction.

L'équipe Di Sante voulait savoir si elle pouvait utiliser un outil d'apprentissage automatique appelé réseau neuronal pour rendre les groupes de renormalisation plus gérables.

Dans le cas des réseaux de neurones, les chercheurs utilisent d'abord des procédures d'apprentissage automatique pour établir des connexions avec le groupe de renormalisation en taille réelle ; puis le réseau de neurones ajuste la force de ces connexions jusqu'à ce qu'il trouve un petit ensemble d'équations qui génèrent le même ensemble d'équations que l'original, la même solution pour de très grands groupes de renormalisation. Nous nous retrouvons avec quatre équations, et même s'il n'y en a que quatre, le résultat du programme capture la physique du modèle de Hubbard.

Di Sante a déclaré : "Un réseau de neurones est essentiellement une machine qui peut découvrir des modèles cachés, et ce résultat a dépassé nos attentes."

La formation des programmes d'apprentissage automatique nécessite beaucoup de puissance de calcul, ils ont donc dépensé cela. plusieurs semaines à réaliser. La bonne nouvelle est que maintenant que leur programme est opérationnel, quelques ajustements peuvent résoudre d’autres problèmes sans avoir à repartir de zéro.

En parlant des orientations futures de la recherche, Di Sante a déclaré qu'il est nécessaire de vérifier l'efficacité de la nouvelle méthode sur des systèmes quantiques plus complexes. En outre, Di Sante affirme qu'il existe de grandes possibilités d'utilisation de la technique dans d'autres domaines concernant les groupes de renormalisation, tels que la cosmologie et les neurosciences.

Présentation de l'article

Nous effectuons une réduction de dimensionnalité basée sur les données sur une fonction à quatre sommets dépendant de l'échelle qui décrit les caractéristiques de flux du groupe de renormalisation fonctionnelle (fRG) du modèle bidimensionnel tt' Hubbard largement étudié sur des cristaux carrés. Ils démontrent qu’une architecture d’apprentissage en profondeur basée sur un solveur d’équation différentielle régulière neuronale (NODE) ​​dans un espace latent de faible dimension peut apprendre efficacement la dynamique fRG décrivant divers états supraconducteurs magnétiques et à ondes D du modèle Hubbard.

Les chercheurs ont en outre proposé une analyse de décomposition des modes dynamiques, qui peut confirmer que quelques modes sont effectivement suffisants pour capturer la dynamique du fRG. L'étude démontre la possibilité d'utiliser l'intelligence artificielle pour extraire des représentations compactes de fonctions pertinentes à quatre sommets électroniques, ce qui constitue l'objectif le plus important pour mettre en œuvre avec succès des méthodes de pointe de la théorie quantique des champs et résoudre des problèmes impliquant plusieurs électrons. L'objet de base de

fRG est la fonction de sommet V(k_1, k_2, k_3), qui doit en principe être calculée et stockée comme une fonction composée de trois variables d'impulsion continues. En étudiant des modèles théoriques spécifiques, le modèle bidimensionnel de Hubbard semble pertinent pour les cuprates et un large éventail de conducteurs organiques. Nous montrons que les représentations de dimension inférieure peuvent capturer le flux fRG de fonctions de sommet de grande dimension.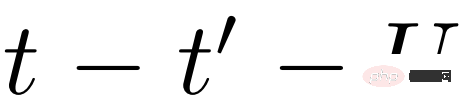

L'état fondamental fRG du modèle Hubbard. L'hamiltonien microscopique considéré par le chercheur est représenté par la formule suivante (1). Les propriétés à 2 particules du modèle

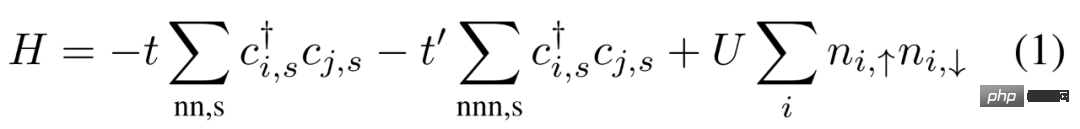
Hubbard sont étudiées à travers un schéma fRG à une boucle de flux de température, où le flux RG de 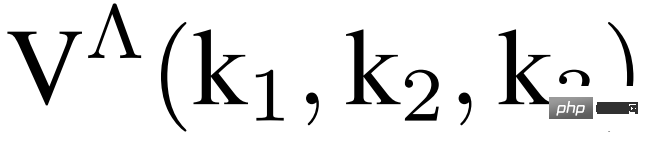est représenté dans l'équation suivante (2).

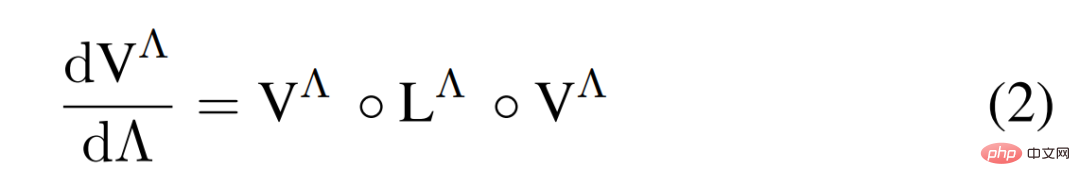
La figure 1 a) ci-dessous est une représentation graphique de l'équation de flux fRG à un anneau de la fonction de sommet à 2 particules V^Λ.

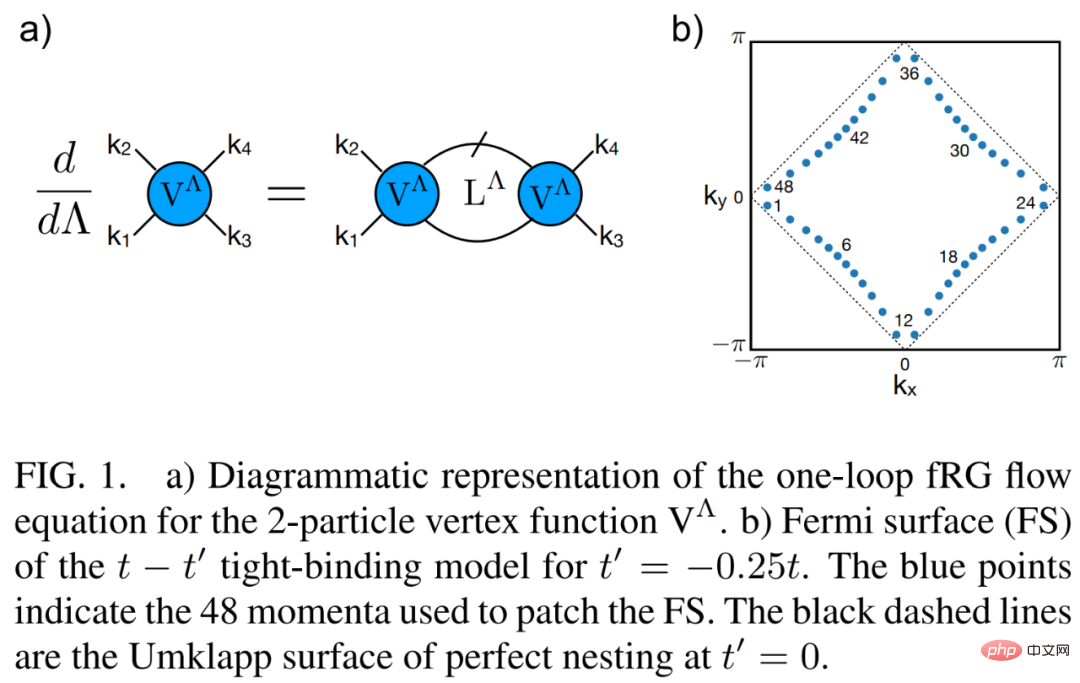
Ensuite, regardons le deep learning fRG. Comme le montre la figure 2 b) ci-dessous, en examinant le couplage 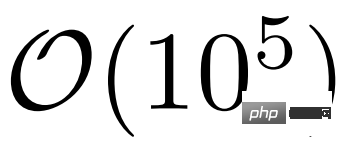de la fonction de sommet à 2 particules avant que le flux fRG ne tende vers un couplage fort et la décomposition approximative en un seul anneau, les chercheurs ont réalisé que beaucoup d'entre eux restent dans le état de bord ou devenir Non pertinent.

Les chercheurs mettent en œuvre un schéma flexible de réduction de dimensionnalité basé sur l'architecture paramétrée NODE adaptée aux problèmes actuels de haute dimension. Cette méthode est présentée dans la figure 2 a) ci-dessous, en se concentrant sur les réseaux de neurones profonds.

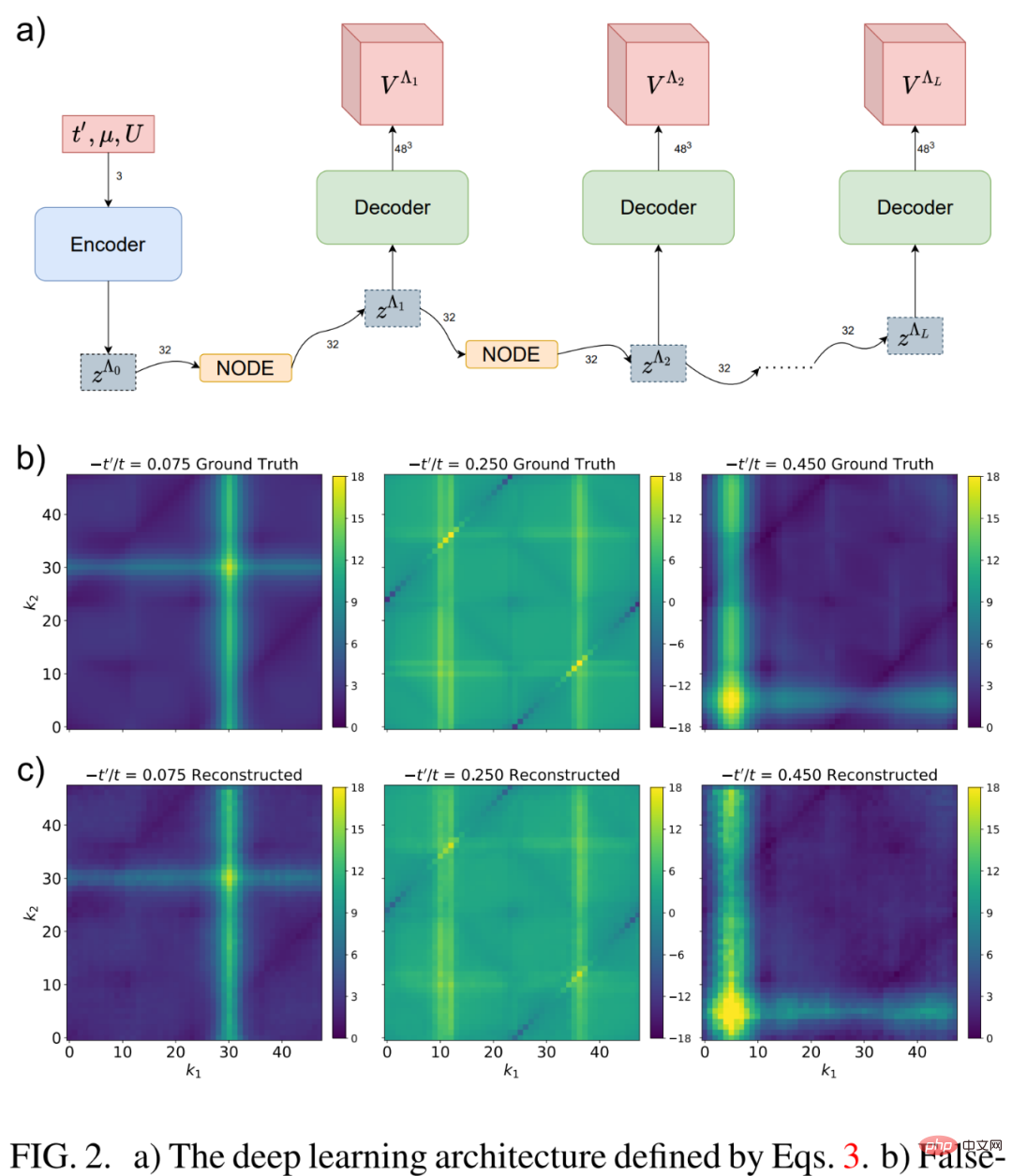
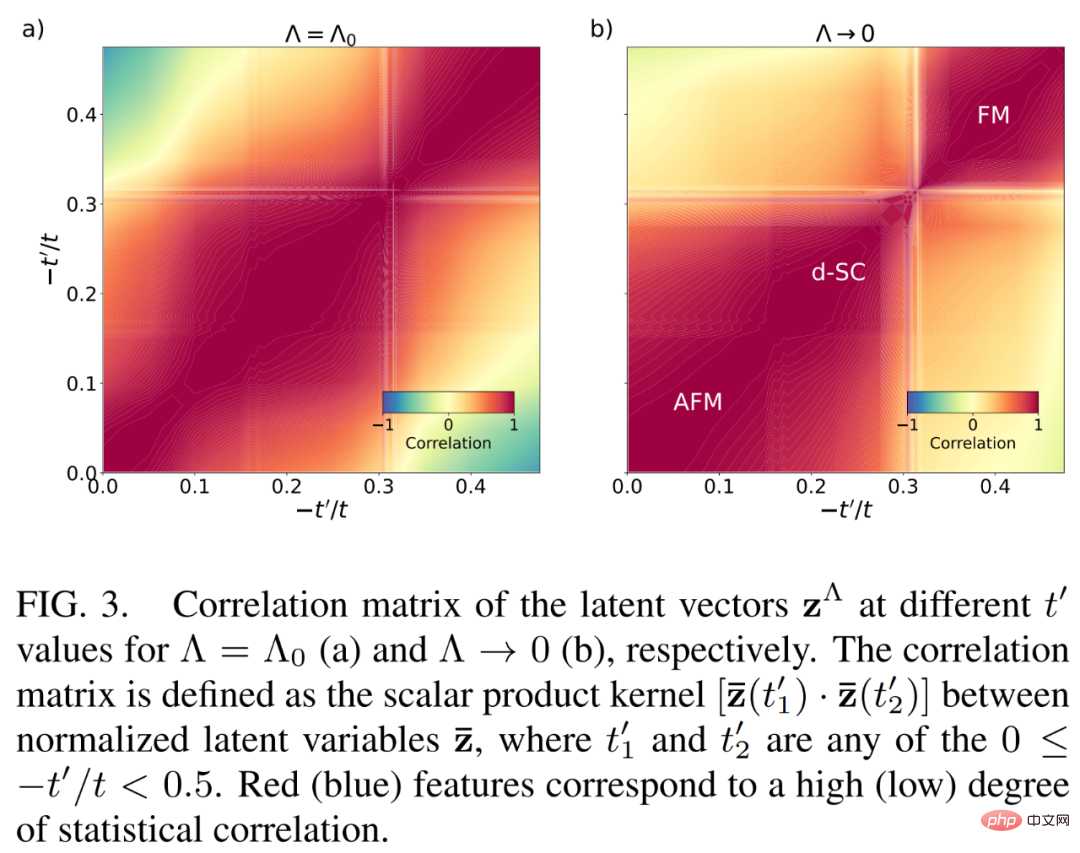
La figure 3 ci-dessous montre trois représentations d'espace latent z statistiquement hautement corrélées en tant que caractéristiques apprises du réseau neuronal NODE au cours de la dynamique fRG de l'espace latent.

Veuillez vous référer au document original pour plus de détails.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!