
La complexité informatique est une mesure des ressources de calcul (temps et espace) consommées par un algorithme spécifique lors de son exécution.
La complexité informatique est divisée en deux catégories :
La complexité temporelle n'est pas une mesure des performances d'un algorithme ou d'un morceau de code. Le temps nécessaire pour s'exécuter sur une machine ou une condition. La complexité temporelle fait généralement référence à la complexité temporelle, qui est une fonction qui décrit qualitativement le temps d'exécution de l'algorithme et nous permet de comparer différents algorithmes sans les exécuter. Par exemple, un algorithme avec O(n) fonctionnera toujours mieux que O(n²) car son taux de croissance est inférieur à O(n²).
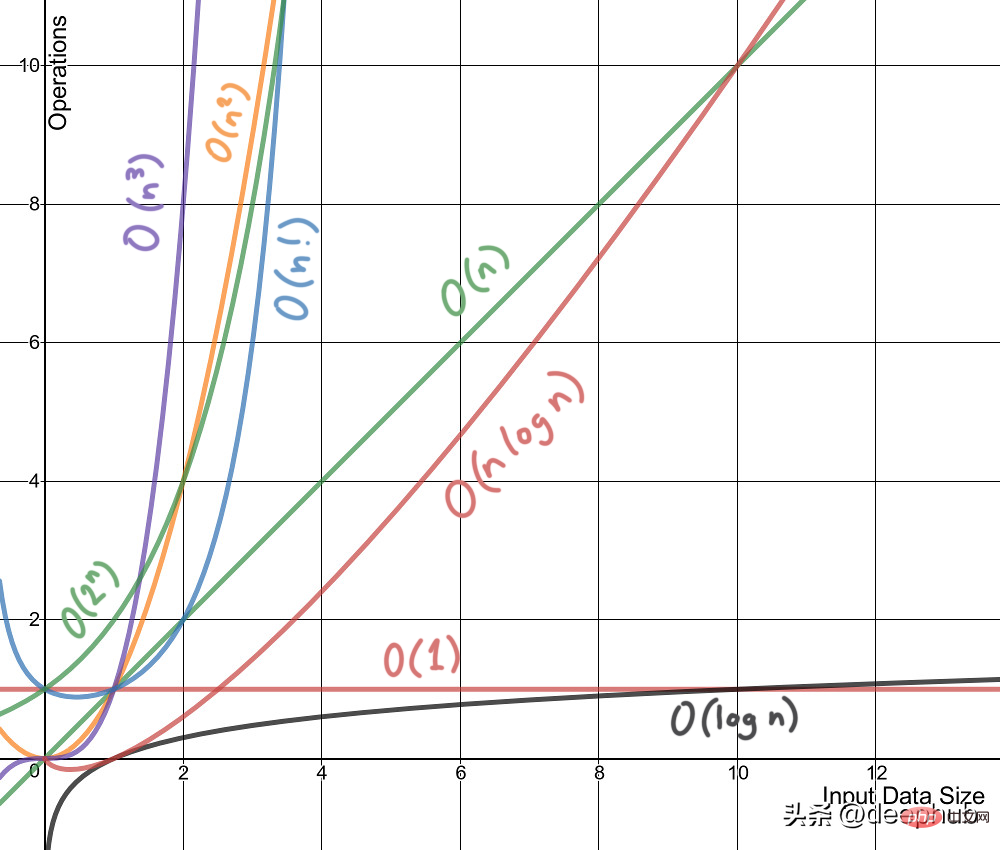
Tout comme la complexité temporelle est une fonction, la complexité spatiale l'est aussi. Conceptuellement, c'est la même chose que la complexité temporelle, il suffit de remplacer le temps par l'espace. Wikipédia définit la complexité spatiale comme :
La complexité spatiale d'un algorithme ou d'un programme informatique est la quantité d'espace de stockage requise pour résoudre une instance d'un problème informatique en fonction du nombre de fonctionnalités en entrée.
Ci-dessous, nous avons compilé la complexité informatique de certains algorithmes d'apprentissage automatique courants.
#🎜🎜 #Complexité de l'espace-temps d'exécution : O(n*f)
kd-tree :8, K-means clustering :
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Algorithme de remplacement de page
Algorithme de remplacement de page
 Comment obtenir la longueur d'un tableau en js
Comment obtenir la longueur d'un tableau en js
 Comment résoudre le problème de l'échec de l'installation de vs2008
Comment résoudre le problème de l'échec de l'installation de vs2008
 Comment verrouiller l'écran sur oppo11
Comment verrouiller l'écran sur oppo11
 Comment résoudre l'erreur 1
Comment résoudre l'erreur 1
 commandes communes iscsiadm
commandes communes iscsiadm
 Quels sont les serveurs exemptés d'enregistrement ?
Quels sont les serveurs exemptés d'enregistrement ?
 Comment vérifier les liens morts d'un site Web
Comment vérifier les liens morts d'un site Web