 Périphériques technologiques
Périphériques technologiques
 IA
IA
 L'apprentissage automatique peut-il vraiment produire des décisions intelligentes ?
L'apprentissage automatique peut-il vraiment produire des décisions intelligentes ?
L'apprentissage automatique peut-il vraiment produire des décisions intelligentes ?
Après trois ans, nous avons achevé en 2022 Judea Pearl, lauréate du Turing Award, professeur d'informatique à l'UCLA, académicien de la National Academy of Sciences, et connu comme le « Père des réseaux bayésiens » Le chef-d'œuvre « Causalité : Modèles » , Raisonnement et Inférence".
La première édition originale de ce livre a été écrite en 2000. Il a été le pionnier de nouvelles idées et méthodes d'analyse causale et d'inférence. Il a été largement salué dès sa publication et a promu la science des données, l'intelligence artificielle, l'apprentissage automatique et la causalité. Les nouvelles révolutions dans des domaines tels que l’analyse ont eu un grand impact sur le monde universitaire.
Plus tard, la deuxième édition a été révisée en 2009. Le contenu a été considérablement modifié en fonction des nouveaux développements de la recherche causale à cette époque. La version originale anglaise du livre que nous traduisons actuellement a été publiée en 2009, il y a donc plus de dix ans.
La publication de la version chinoise de ce livre aidera les universitaires, étudiants et praticiens chinois dans divers domaines à comprendre et à maîtriser le contenu lié aux modèles causals, au raisonnement et à l'inférence. Surtout à l'ère actuelle où les statistiques et l'apprentissage automatique sont populaires, comment réaliser la transformation de « l'ajustement des données » à la « compréhension des données » ? Comment passer de l’hypothèse actuellement dominante selon laquelle « toute connaissance vient des données elles-mêmes » à un tout nouveau paradigme d’apprentissage automatique au cours de la prochaine décennie ? Cela déclenchera-t-il une « deuxième révolution de l’intelligence artificielle » ?
Tout comme le prix Turing a été décerné à Pearl, son travail a été évalué comme « une contribution fondamentale au domaine de l'intelligence artificielle ». Il a proposé des algorithmes de raisonnement probabiliste et causal, qui ont complètement changé l'orientation de l'intelligence artificielle basée à l'origine sur des règles. et la logique." Nous espérons que ce paradigme apportera de nouvelles orientations techniques et donnera un élan à l'apprentissage automatique, et qu'il jouera finalement un rôle dans les applications pratiques.
正Comme l'a dit Pearl, « l'ajustement des données domine actuellement fermement les domaines actuels des statistiques et de l'apprentissage automatique et constitue le principal paradigme de recherche pour la plupart des chercheurs en apprentissage automatique aujourd'hui, en particulier ceux engagés dans "les chercheurs en isme, en apprentissage profond et en technologie de réseau neuronal. » Ce paradigme centré sur « l’ajustement des données » a obtenu un succès remarquable dans des domaines d’application tels que la vision par ordinateur, la reconnaissance vocale et la conduite autonome. Cependant, de nombreux chercheurs dans le domaine de la science des données ont également réalisé que, dans la pratique actuelle, l’apprentissage automatique ne peut pas produire le type de compréhension requis pour une prise de décision intelligente. Ces questions incluent : la robustesse, la transférabilité, l’interprétabilité, etc. Regardons un exemple ci-dessous.
1. Les statistiques sont-elles fiables ?
Ces dernières années, de nombreux acteurs des auto-médias se prennent pour des statisticiens. Parce que "l'ajustement des données" et "toute connaissance vient des données elles-mêmes" fournissent une base statistique pour de nombreuses décisions importantes. Cependant, nous devons être prudents lors de cette analyse. Après tout, les choses ne sont pas toujours ce qu’elles paraissent à première vue ! Une affaire étroitement liée à nos vies. Il y a dix ans, le prix des logements dans le centre-ville était de 8 000 yuans/mètre carré, pour un total de 10 millions de mètres carrés vendus ; dans la zone de haute technologie, il était de 4 000 yuans/mètre carré, pour un total de 1 million de mètres carrés. mètres vendus ; dans l'ensemble, le prix moyen des logements dans la ville était de 7 636 yuans/mètre carré. Aujourd'hui, le prix dans le centre-ville est de 10 000 yuans/mètre carré, mais comme l'offre de terrains dans le centre-ville est moindre, seuls 2 millions de mètres carrés ont été vendus ; la zone de haute technologie coûte 6 000 yuans/mètre carré, mais parce que il y a plus de terrains nouvellement aménagés, 20 millions de mètres carrés ont été vendus ; dans l'ensemble, le prix moyen des logements dans la ville est maintenant de 6 363 yuans/mètre carré. Par conséquent, si l’on considère les différents domaines, les prix de l’immobilier ont augmenté individuellement, mais si l’on considère l’ensemble, des doutes subsistent : pourquoi les prix de l’immobilier ont-ils baissé maintenant ?
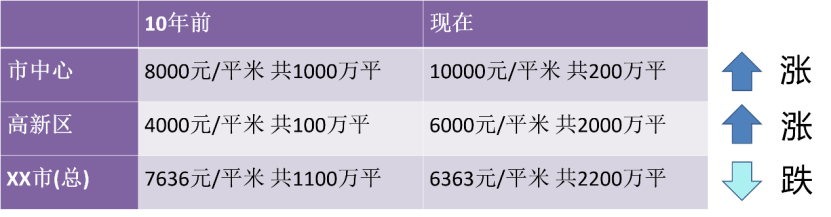
Figure 1 La tendance des prix de l'immobilier est divisée en différentes régions et est contraire à la conclusion générale
Nous savons que ce phénomène s'appelle le paradoxe de Simpson. Ces cas montrent clairement comment nous pouvons obtenir des modèles et des conclusions complètement erronés à partir de données statistiques lorsque nous ne disposons pas de suffisamment de variables observées. Dans le cas de cette pandémie, nous obtenons généralement des statistiques à l’échelle nationale. Si nous regroupions par région, ville ou comté, nous pourrions arriver à des conclusions très différentes. Partout au pays, nous pouvons observer une baisse du nombre de cas de COVID-19, même si certaines régions connaissent une augmentation des cas (ce qui pourrait signaler le début de la prochaine vague). Cela peut également se produire s’il existe des groupes très différents, comme par exemple des zones avec des populations très différentes. Dans les données nationales, les augmentations de cas dans les zones moins densément peuplées peuvent être éclipsées par les baisses dans les zones plus densément peuplées.
Des problèmes statistiques similaires basés sur « l'ajustement des données » abondent. Prenons les deux exemples intéressants suivants.
Si nous collectons chaque année des données sur le nombre de films joués par Nicolas Cage et le nombre de noyades aux États-Unis, nous constaterons que ces deux variables sont fortement corrélées et que l'ajustement des données est extrêmement élevé .
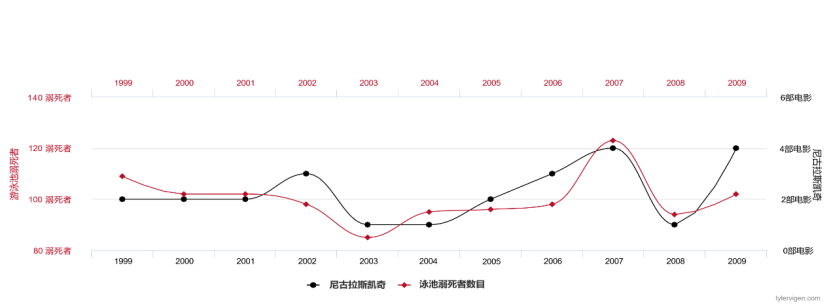
Figure 2 Le nombre de films dans lesquels Nicolas Cage apparaît chaque année et le nombre de personnes qui se noient aux États-Unis États#🎜 🎜#
Si nous collectons des données sur les ventes de lait par habitant et le nombre de lauréats du prix Nobel dans chaque pays, nous constaterons que ces deux variables sont fortement corrélées.
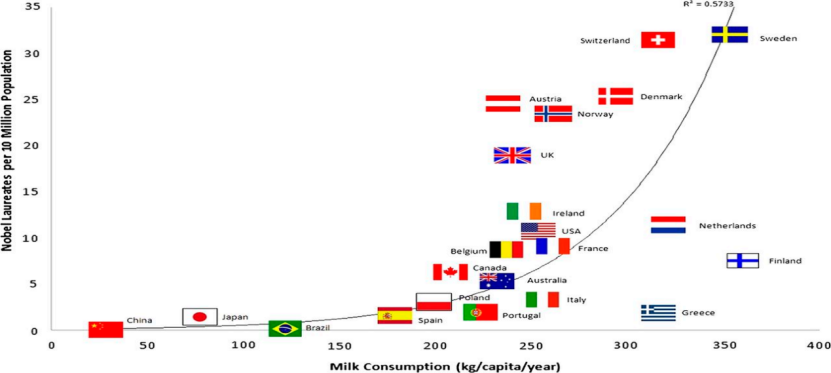
Figure 3 Consommation de lait par habitant et nombre de prix Nobel#🎜🎜 #
D'après notre bon sens d'êtres humains, ce sont des pseudo-corrélations voire des paradoxes. Mais du point de vue des mathématiques et de la théorie des probabilités, les cas présentant de fausses corrélations ou paradoxes ne posent pas de problème, tant d’un point de vue statistique que informatique. Quiconque ayant une certaine base causale sait que cela se produit parce qu’il existe des variables dites cachées, des facteurs confondants inobservés, cachés dans les données.
Perl a donné un paradigme de solution dans "La théorie de cause à effet", a analysé et dérivé les problèmes ci-dessus en détail et a souligné le lien entre la cause et l'effet et les statistiques. La différence essentielle est que l'analyse causale et l'inférence sont toujours basées sur le contexte des statistiques. Pearl a proposé le modèle de calcul de base des opérations d'intervention (opérateurs), incluant le principe de la porte dérobée et des formules de calcul spécifiques. Il s'agit actuellement de la description la plus mathématique de la causalité. "La causalité et les concepts associés (tels que la randomisation, la confusion, l'intervention, etc.) ne sont pas des concepts statistiques." Il s'agit d'un principe de base qui traverse la pensée de l'analyse causale de Pearl, que Pearl appelle le premier principe [2].
Ainsi, les méthodes actuelles d'apprentissage automatique basées sur les données, en particulier les algorithmes qui s'appuient fortement sur des méthodes statistiques, sont très susceptibles d'apprendre la moitié des modèles. , des résultats trompeurs ou contraires. En effet, ces modèles ont tendance à apprendre en fonction de la distribution des données observées plutôt que du mécanisme par lequel les données sont générées.
2. Trois problèmes que le machine learning doit résoudre de toute urgence
Robustesse :Avec La popularité des méthodes d'apprentissage profond, de la recherche en vision par ordinateur, du traitement du langage naturel et de la reconnaissance vocale a largement fait appel aux structures de réseau neuronal profond de pointe. Mais il reste un problème à long terme : dans le monde réel, la distribution des données que nous collectons est généralement rarement complète et peut être incompatible avec la distribution dans le monde réel. Dans les applications de vision par ordinateur, la distribution des données des ensembles d'apprentissage et des ensembles de tests peut être affectée par des facteurs tels que la différence de pixels, la qualité de la compression ou le déplacement, la rotation ou l'angle de la caméra. Ces variables sont en réalité des questions d’« intervention » dans le concept de cause à effet. À partir de là, des algorithmes simples ont été proposés pour simuler des interventions afin de tester spécifiquement la capacité de généralisation des modèles de classification et de reconnaissance, tels que le décalage spatial, le flou, les changements de luminosité ou de contraste, le contrôle et la rotation de l'arrière-plan et l'acquisition dans plusieurs environnements d'images, etc. Jusqu’à présent, bien que nous ayons réalisé certains progrès en termes de robustesse en utilisant des méthodes telles que l’augmentation des données, la pré-formation et l’apprentissage auto-supervisé, il n’existe pas de consensus clair sur la manière de résoudre ces problèmes. Il a été avancé que ces corrections pourraient ne pas être suffisantes et que généraliser au-delà de l'hypothèse indépendante et identiquement distribuée nécessite d'apprendre non seulement les associations statistiques entre les variables, mais également les modèles causals sous-jacents qui clarifient les mécanismes par lesquels les données ont été générées et permettent la simulation en intervenant. concepts Modifications de la distribution.
Transférabilité : La compréhension des objets par les bébés est basée sur le suivi d'objets qui se comportent de manière cohérente au fil du temps. Cette approche permet aux bébés d'apprendre rapidement de nouvelles tâches à mesure qu'ils en apprennent davantage. et la compréhension intuitive des objets peut être réutilisée. De même, être capable de résoudre efficacement des tâches du monde réel nécessite de réutiliser les connaissances et les compétences acquises dans de nouveaux scénarios. La recherche a prouvé que les systèmes d’apprentissage automatique qui apprennent les connaissances environnementales sont plus efficaces et plus polyvalents. Si nous modélisons le monde réel, de nombreux modules présentent un comportement similaire dans différentes tâches et environnements. Ainsi, face à un nouvel environnement ou à une nouvelle tâche, les humains ou les machines n’auront peut-être besoin que d’ajuster quelques modules dans leur représentation interne. Lors de l'apprentissage d'un modèle causal, moins d'échantillons sont nécessaires pour s'adapter à de nouveaux environnements ou tâches, car la plupart des connaissances (c'est-à-dire les modules) peuvent être réutilisées sans formation supplémentaire.
Interprétabilité : L'interprétabilité est un concept subtil qui ne peut être entièrement décrit en utilisant uniquement le langage de la logique booléenne ou des probabilités statistiques. Il nécessite des concepts intermédiaires, voire contrefactuels. La définition de la manipulabilité dans la causalité se concentre sur le fait que les probabilités conditionnelles (« Voir les gens ouvrir leur parapluie indique qu'il pleut ») ne peuvent pas prédire de manière fiable le résultat d'une intervention active (« Ranger ses parapluies n'empêche pas qu'il pleuve »). La causalité est considérée comme une partie intégrante de la chaîne de raisonnement, qui peut fournir des prédictions pour des situations très éloignées de la distribution observée, et peut même fournir des conclusions pour des scénarios purement hypothétiques. En ce sens, découvrir des relations causales signifie obtenir des connaissances fiables qui ne sont pas limitées par la distribution des données observées et les tâches de formation, fournissant ainsi une spécification sans ambiguïté pour un apprentissage interprétable.
3. Trois niveaux de modélisation de l'apprentissage causal
Plus précisément, les modèles d'apprentissage automatique basés sur des modèles statistiques ne peuvent modéliser que des corrélations. et les relations de corrélation changent souvent avec les changements dans la distribution des données ; tandis que les modèles causals sont basés sur une modélisation des relations causales, qui capture l'essence de la génération de données et reflète la relation entre les mécanismes de génération de données. Ces relations sont plus robustes. Dans la théorie de la décision, par exemple, la distinction entre causalité et statistiques est plus claire. Il existe deux types de problèmes dans la théorie de la décision. L’un consiste à connaître l’environnement actuel, à planifier une intervention et à prédire le résultat. L’autre type consiste à connaître l’environnement et les résultats actuels et à en déduire les causes. Le premier est appelé problème consécutif, et le second est appelé problème d’enlèvement [3].
Capacité prédictive dans des conditions indépendantes et identiquement distribuées
Les modèles statistiques ne sont que des descriptions superficielles du monde réel observé car ils se concentrent uniquement sur les relations connexes . Pour les échantillons et les étiquettes, nous pouvons utiliser des estimations pour répondre à des questions telles que : « Quelle est la probabilité qu'il y ait un chien sur cette photo particulière ? » « Compte tenu de certains symptômes, quelle est la probabilité d'insuffisance cardiaque ? ». Il est possible de répondre à ces questions en observant suffisamment de données i.i.d. Bien que les algorithmes d’apprentissage automatique puissent bien faire ces choses, des prédictions précises ne suffisent pas pour notre prise de décision, et l’apprentissage causal fournit un complément utile. Comme pour l'exemple précédent, la fréquence de Nicolas Cage dans les films est positivement corrélée au taux de mortalité par noyade aux États-Unis. Nous pouvons en effet former un modèle d'apprentissage statistique pour prédire le taux de mortalité par noyade aux États-Unis en fonction de la fréquence des noyades. Nicolas Cage joue dans des films, mais évidemment il n'y a pas de relation causale directe entre les deux. Les modèles statistiques ne sont précis que lorsqu'ils sont distribués de manière indépendante et identique. Si nous intervenons pour modifier la distribution des données, cela entraînera des erreurs dans le modèle d'apprentissage statistique.
Pouvoir prédictif sous changement de distribution/intervention
Nous discutons plus en détail du problème de l'intervention, qui est plus difficile car l'intervention (opération) nous sort de l'hypothèse d'une distribution indépendante et identique dans l'apprentissage statistique. Pour reprendre l'exemple de Nicolas Cage, « L'augmentation du nombre de films de Nicolas Cage cette année augmentera-t-elle le taux de noyade aux États-Unis est-elle une question d'intervention ? De toute évidence, l’intervention humaine entraînera une modification de la distribution des données et les conditions de survie de l’apprentissage statistique seront brisées, ce qui entraînera un échec. D’un autre côté, si nous pouvons apprendre un modèle prédictif en présence d’une intervention, cela nous permettra potentiellement d’obtenir un modèle plus robuste aux changements de distribution dans des contextes réels. En fait, ce qu'on appelle l'intervention n'a rien de nouveau ici. Beaucoup de choses elles-mêmes changent avec le temps, comme les préférences d'intérêt des gens, ou il y a une inadéquation dans la distribution de l'ensemble de formation du modèle et de l'ensemble de test lui-même. Comme nous l'avons mentionné précédemment, la robustesse des réseaux de neurones fait l'objet de plus en plus d'attention et est devenue un sujet de recherche étroitement lié à l'inférence causale. La prédiction en cas de changement de distribution ne peut pas se limiter à atteindre une grande précision sur l'ensemble de test. Si nous espérons utiliser des algorithmes d'apprentissage automatique dans des applications pratiques, nous devons alors croire que les résultats de prédiction du modèle changeront également lorsque les conditions environnementales changeront. Précis. Les catégories de changements de distribution dans les applications pratiques peuvent être diverses. Un modèle n'obtient de bons résultats que sur certains ensembles de tests ne signifie pas que nous pouvons faire confiance à ce modèle dans n'importe quelle situation. Ces ensembles de tests peuvent simplement s'adapter à la distribution de l'échantillon. . Pour pouvoir faire confiance aux modèles prédictifs dans autant de situations que possible, nous devons utiliser des modèles capables de répondre aux questions d’intervention, du moins pas uniquement en utilisant des modèles d’apprentissage statistique.
La capacité de répondre à des questions contrefactuelles
Les questions contrefactuelles impliquent de raisonner sur les raisons pour lesquelles les choses se sont produites, d'imaginer les conséquences de l'exécution de différentes actions, et à partir de là, vous pouvez décider quelles actions entreprendre pour obtenir les résultats souhaités. Répondre à des questions contrefactuelles est plus difficile qu’une intervention, mais cela constitue également un défi crucial pour l’IA. Si une question d'intervention est « Qu'arriverait-il au risque d'insuffisance cardiaque d'un patient si nous commencions à faire de l'exercice régulièrement maintenant ? », la question contrefactuelle correspondante est « Et si ce patient qui souffrait déjà d'insuffisance cardiaque commençait à faire de l'exercice il y a un an ? , aura-t-il toujours une insuffisance cardiaque ? » De toute évidence, répondre à de telles questions contrefactuelles est très important pour l'apprentissage par renforcement. Ils peuvent réfléchir à leurs propres décisions, formuler des hypothèses contrefactuelles, puis les vérifier par la pratique, tout comme notre science. La recherche est la même.
4. Application de l'apprentissage causal
Enfin, voyons comment appliquer l'apprentissage causal dans divers domaines. Le prix Nobel d'économie 2021 a été décerné à Joshua D. Angrist et Guido W. Imbens pour leurs « contributions méthodologiques à l'analyse des relations causales ». Ils étudient l’application de l’inférence causale en économie empirique du travail. Le comité de sélection du prix Nobel d'économie estime que « les expériences naturelles (expériences randomisées ou contrôlées) peuvent aider à répondre à des questions importantes », mais comment « utiliser les données d'observation pour répondre aux relations causales » est plus difficile. Une question importante en économie est celle de la causalité. Par exemple, comment les immigrants affectent-ils les perspectives du marché du travail des locaux ? Les études supérieures peuvent-elles augmenter les revenus ? Quel impact le salaire minimum a-t-il sur les perspectives d’emploi des travailleurs qualifiés ? Il est difficile de répondre à ces questions car nous ne disposons pas des bons moyens d’interpréter les contrefactuels.
Depuis les années 1970, les statisticiens ont inventé un cadre de calcul de « contrefactuels » pour révéler l’effet causal entre deux variables. Sur cette base, les économistes ont développé des méthodes telles que la régression de discontinuité, la différence de différences et le score de propension, et les ont largement appliquées dans la recherche causale sur diverses questions de politique économique. Des textes religieux du VIe siècle à l’apprentissage automatique causal en 2021, en passant par le traitement causal du langage naturel, nous pouvons utiliser l’apprentissage automatique, les statistiques et l’économétrie pour modéliser les effets causals. L'analyse en économie et autres sciences sociales tourne principalement autour de l'estimation des effets causals, c'est-à-dire l'effet d'intervention d'une variable caractéristique sur la variable de résultat. En fait, dans la plupart des cas, ce qui nous intéresse est ce qu'on appelle l'effet d'intervention. L'effet de l'intervention fait référence à l'impact causal d'une intervention ou d'un traitement sur la variable de résultat. Par exemple, en économie, l’un des effets d’intervention les plus analysés est l’impact causal des subventions accordées aux entreprises sur leurs revenus. À cette fin, Rubin a proposé le cadre de résultats potentiels.
Bien que les économistes et autres spécialistes des sciences sociales soient plus capables d’estimer avec précision les effets causals que de prédire, ils s’intéressent également aux avantages prédictifs des méthodes d’apprentissage automatique. Par exemple, des capacités de prédiction d'échantillons précises ou la capacité de gérer un grand nombre de fonctionnalités. Mais comme nous l’avons vu, les modèles classiques d’apprentissage automatique ne sont pas conçus pour estimer les effets causals, et l’utilisation de méthodes prédictives prêtes à l’emploi issues de l’apprentissage automatique peut conduire à des estimations biaisées des effets causals. Ensuite, nous devons améliorer les techniques d’apprentissage automatique existantes pour tirer parti de l’apprentissage automatique afin d’estimer de manière continue et efficace les effets causals, ce qui a conduit à la naissance de l’apprentissage automatique causal !
Actuellement, l'apprentissage automatique causal peut être grossièrement divisé en deux directions de recherche selon le type d'effets causals à estimer. Une orientation importante consiste à améliorer les méthodes d’apprentissage automatique pour obtenir des estimations impartiales et cohérentes des effets moyens des interventions. Les modèles de ce domaine de recherche tentent de répondre aux questions suivantes : Quelle est la réponse moyenne d'un client à une campagne marketing ? Quel est l’impact moyen d’un changement de prix sur les ventes ? En outre, un autre axe de développement dans la recherche sur l’apprentissage automatique causal consiste à améliorer les méthodes d’apprentissage automatique pour révéler la spécificité des effets de l’intervention, c’est-à-dire identifier des sous-populations d’individus ayant des effets d’intervention supérieurs ou inférieurs à la moyenne. Ce type de modèle vise à répondre à la question suivante : Quels clients répondent le plus aux campagnes marketing ? Comment l’impact des changements de prix sur les ventes varie-t-il en fonction de l’âge du client ?
En plus de ces exemples vivants, nous pouvons également sentir qu'une raison plus profonde pour laquelle l'apprentissage automatique causal suscite l'intérêt des data scientists est la capacité de généralisation du modèle. Les modèles d’apprentissage automatique qui décrivent les relations causales entre les données peuvent être généralisés à de nouveaux environnements, mais cela reste aujourd’hui l’un des plus grands défis de l’apprentissage automatique.
Perl analyse ces problèmes à un niveau plus profond et estime que si les machines ne peuvent pas raisonner de manière causale, nous n'atteindrons jamais une véritable intelligence artificielle au niveau humain, car la causalité est un mécanisme clé permettant à nous, humains, de traiter et de comprendre le monde complexe qui nous entoure. . Pearl écrit dans la préface de la version chinoise de « On Causality » qu'« au cours de la prochaine décennie, ce cadre sera combiné avec les systèmes d'apprentissage automatique existants, déclenchant potentiellement une « seconde révolution causale ». lecteurs à participer activement à cette révolution à venir.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Bytedance Cutting lance le super abonnement SVIP : 499 yuans pour un abonnement annuel continu, offrant une variété de fonctions d'IA
Jun 28, 2024 am 03:51 AM
Bytedance Cutting lance le super abonnement SVIP : 499 yuans pour un abonnement annuel continu, offrant une variété de fonctions d'IA
Jun 28, 2024 am 03:51 AM
Ce site a rapporté le 27 juin que Jianying est un logiciel de montage vidéo développé par FaceMeng Technology, une filiale de ByteDance. Il s'appuie sur la plateforme Douyin et produit essentiellement du contenu vidéo court pour les utilisateurs de la plateforme. Il est compatible avec iOS, Android et. Windows, MacOS et autres systèmes d'exploitation. Jianying a officiellement annoncé la mise à niveau de son système d'adhésion et a lancé un nouveau SVIP, qui comprend une variété de technologies noires d'IA, telles que la traduction intelligente, la mise en évidence intelligente, l'emballage intelligent, la synthèse humaine numérique, etc. En termes de prix, les frais mensuels pour le clipping SVIP sont de 79 yuans, les frais annuels sont de 599 yuans (attention sur ce site : équivalent à 49,9 yuans par mois), l'abonnement mensuel continu est de 59 yuans par mois et l'abonnement annuel continu est de 59 yuans par mois. est de 499 yuans par an (équivalent à 41,6 yuans par mois) . En outre, le responsable de Cut a également déclaré que afin d'améliorer l'expérience utilisateur, ceux qui se sont abonnés au VIP d'origine
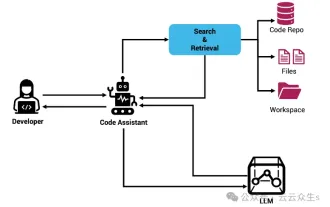 Assistant de codage d'IA augmenté par le contexte utilisant Rag et Sem-Rag
Jun 10, 2024 am 11:08 AM
Assistant de codage d'IA augmenté par le contexte utilisant Rag et Sem-Rag
Jun 10, 2024 am 11:08 AM
Améliorez la productivité, l’efficacité et la précision des développeurs en intégrant une génération et une mémoire sémantique améliorées par la récupération dans les assistants de codage IA. Traduit de EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, auteur JanakiramMSV. Bien que les assistants de programmation d'IA de base soient naturellement utiles, ils ne parviennent souvent pas à fournir les suggestions de code les plus pertinentes et les plus correctes, car ils s'appuient sur une compréhension générale du langage logiciel et des modèles d'écriture de logiciels les plus courants. Le code généré par ces assistants de codage est adapté à la résolution des problèmes qu’ils sont chargés de résoudre, mais n’est souvent pas conforme aux normes, conventions et styles de codage des équipes individuelles. Cela aboutit souvent à des suggestions qui doivent être modifiées ou affinées pour que le code soit accepté dans l'application.
 Sept questions d'entretien technique Cool GenAI et LLM
Jun 07, 2024 am 10:06 AM
Sept questions d'entretien technique Cool GenAI et LLM
Jun 07, 2024 am 10:06 AM
Pour en savoir plus sur l'AIGC, veuillez visiter : 51CTOAI.x Community https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou est différent de la banque de questions traditionnelle que l'on peut voir partout sur Internet. nécessite de sortir des sentiers battus. Les grands modèles linguistiques (LLM) sont de plus en plus importants dans les domaines de la science des données, de l'intelligence artificielle générative (GenAI) et de l'intelligence artificielle. Ces algorithmes complexes améliorent les compétences humaines et stimulent l’efficacité et l’innovation dans de nombreux secteurs, devenant ainsi la clé permettant aux entreprises de rester compétitives. LLM a un large éventail d'applications. Il peut être utilisé dans des domaines tels que le traitement du langage naturel, la génération de texte, la reconnaissance vocale et les systèmes de recommandation. En apprenant de grandes quantités de données, LLM est capable de générer du texte
 Le réglage fin peut-il vraiment permettre au LLM d'apprendre de nouvelles choses : l'introduction de nouvelles connaissances peut amener le modèle à produire davantage d'hallucinations
Jun 11, 2024 pm 03:57 PM
Le réglage fin peut-il vraiment permettre au LLM d'apprendre de nouvelles choses : l'introduction de nouvelles connaissances peut amener le modèle à produire davantage d'hallucinations
Jun 11, 2024 pm 03:57 PM
Les grands modèles linguistiques (LLM) sont formés sur d'énormes bases de données textuelles, où ils acquièrent de grandes quantités de connaissances du monde réel. Ces connaissances sont intégrées à leurs paramètres et peuvent ensuite être utilisées en cas de besoin. La connaissance de ces modèles est « réifiée » en fin de formation. À la fin de la pré-formation, le modèle arrête effectivement d’apprendre. Alignez ou affinez le modèle pour apprendre à exploiter ces connaissances et répondre plus naturellement aux questions des utilisateurs. Mais parfois, la connaissance du modèle ne suffit pas, et bien que le modèle puisse accéder à du contenu externe via RAG, il est considéré comme bénéfique de l'adapter à de nouveaux domaines grâce à un réglage fin. Ce réglage fin est effectué à l'aide de la contribution d'annotateurs humains ou d'autres créations LLM, où le modèle rencontre des connaissances supplémentaires du monde réel et les intègre.
 Afin de fournir un nouveau système de référence et d'évaluation de questions-réponses scientifiques et complexes pour les grands modèles, l'UNSW, Argonne, l'Université de Chicago et d'autres institutions ont lancé conjointement le cadre SciQAG.
Jul 25, 2024 am 06:42 AM
Afin de fournir un nouveau système de référence et d'évaluation de questions-réponses scientifiques et complexes pour les grands modèles, l'UNSW, Argonne, l'Université de Chicago et d'autres institutions ont lancé conjointement le cadre SciQAG.
Jul 25, 2024 am 06:42 AM
L'ensemble de données ScienceAI Question Answering (QA) joue un rôle essentiel dans la promotion de la recherche sur le traitement du langage naturel (NLP). Des ensembles de données d'assurance qualité de haute qualité peuvent non seulement être utilisés pour affiner les modèles, mais également évaluer efficacement les capacités des grands modèles linguistiques (LLM), en particulier la capacité à comprendre et à raisonner sur les connaissances scientifiques. Bien qu’il existe actuellement de nombreux ensembles de données scientifiques d’assurance qualité couvrant la médecine, la chimie, la biologie et d’autres domaines, ces ensembles de données présentent encore certaines lacunes. Premièrement, le formulaire de données est relativement simple, et la plupart sont des questions à choix multiples. Elles sont faciles à évaluer, mais limitent la plage de sélection des réponses du modèle et ne peuvent pas tester pleinement la capacité du modèle à répondre aux questions scientifiques. En revanche, les questions et réponses ouvertes
 Cinq écoles d'apprentissage automatique que vous ne connaissez pas
Jun 05, 2024 pm 08:51 PM
Cinq écoles d'apprentissage automatique que vous ne connaissez pas
Jun 05, 2024 pm 08:51 PM
L'apprentissage automatique est une branche importante de l'intelligence artificielle qui donne aux ordinateurs la possibilité d'apprendre à partir de données et d'améliorer leurs capacités sans être explicitement programmés. L'apprentissage automatique a un large éventail d'applications dans divers domaines, de la reconnaissance d'images et du traitement du langage naturel aux systèmes de recommandation et à la détection des fraudes, et il change notre façon de vivre. Il existe de nombreuses méthodes et théories différentes dans le domaine de l'apprentissage automatique, parmi lesquelles les cinq méthodes les plus influentes sont appelées les « Cinq écoles d'apprentissage automatique ». Les cinq grandes écoles sont l’école symbolique, l’école connexionniste, l’école évolutionniste, l’école bayésienne et l’école analogique. 1. Le symbolisme, également connu sous le nom de symbolisme, met l'accent sur l'utilisation de symboles pour le raisonnement logique et l'expression des connaissances. Cette école de pensée estime que l'apprentissage est un processus de déduction inversée, à travers les connaissances existantes.
 Les performances de SOTA, la méthode d'IA de prédiction d'affinité protéine-ligand multimodale de Xiamen, combinent pour la première fois des informations sur la surface moléculaire
Jul 17, 2024 pm 06:37 PM
Les performances de SOTA, la méthode d'IA de prédiction d'affinité protéine-ligand multimodale de Xiamen, combinent pour la première fois des informations sur la surface moléculaire
Jul 17, 2024 pm 06:37 PM
Editeur | KX Dans le domaine de la recherche et du développement de médicaments, il est crucial de prédire avec précision et efficacité l'affinité de liaison des protéines et des ligands pour le criblage et l'optimisation des médicaments. Cependant, les études actuelles ne prennent pas en compte le rôle important des informations sur la surface moléculaire dans les interactions protéine-ligand. Sur cette base, des chercheurs de l'Université de Xiamen ont proposé un nouveau cadre d'extraction de caractéristiques multimodales (MFE), qui combine pour la première fois des informations sur la surface des protéines, la structure et la séquence 3D, et utilise un mécanisme d'attention croisée pour comparer différentes modalités. alignement. Les résultats expérimentaux démontrent que cette méthode atteint des performances de pointe dans la prédiction des affinités de liaison protéine-ligand. De plus, les études d’ablation démontrent l’efficacité et la nécessité des informations sur la surface des protéines et de l’alignement des caractéristiques multimodales dans ce cadre. Les recherches connexes commencent par "S
 Préparant des marchés tels que l'IA, GlobalFoundries acquiert la technologie du nitrure de gallium de Tagore Technology et les équipes associées
Jul 15, 2024 pm 12:21 PM
Préparant des marchés tels que l'IA, GlobalFoundries acquiert la technologie du nitrure de gallium de Tagore Technology et les équipes associées
Jul 15, 2024 pm 12:21 PM
Selon les informations de ce site Web du 5 juillet, GlobalFoundries a publié un communiqué de presse le 1er juillet de cette année, annonçant l'acquisition de la technologie de nitrure de gallium (GaN) et du portefeuille de propriété intellectuelle de Tagore Technology, dans l'espoir d'élargir sa part de marché dans l'automobile et Internet. des objets et des domaines d'application des centres de données d'intelligence artificielle pour explorer une efficacité plus élevée et de meilleures performances. Alors que des technologies telles que l’intelligence artificielle générative (GenerativeAI) continuent de se développer dans le monde numérique, le nitrure de gallium (GaN) est devenu une solution clé pour une gestion durable et efficace de l’énergie, notamment dans les centres de données. Ce site Web citait l'annonce officielle selon laquelle, lors de cette acquisition, l'équipe d'ingénierie de Tagore Technology rejoindrait GF pour développer davantage la technologie du nitrure de gallium. g





