Analyse de code d'exemple d'algorithme de recherche et de tri Python-Tutoriel Python-php.cn

Recherche

Recherche binaire

Recherche binaire est un algorithme de recherche permettant de trouver un élément spécifique dans un tableau ordonné. Le processus de recherche commence à partir de l'élément du milieu du tableau, et si l'élément du milieu s'avère être l'élément à trouver, le processus de recherche se termine si un élément spécifique est supérieur ou inférieur à l'élément du milieu, la recherche est effectuée dans ; la moitié du tableau qui est supérieure ou inférieure à l'élément du milieu, et tout comme au début, démarrez la comparaison à partir de l'élément du milieu. Si le tableau est vide à une certaine étape, cela signifie qu'il est introuvable. Cet algorithme de recherche réduit la plage de recherche de moitié à chaque comparaison.

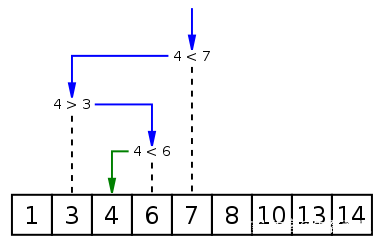
Analyse de code dexemple dalgorithme de recherche et de tri Python

# 返回 x 在 arr 中的索引，如果不存在返回 -1
def binarySearch (arr, l, r, x):
    # 基本判断
    if r >= l:
        mid = int(l + (r - l)/2)
        # 元素整好的中间位置
        if arr[mid] == x:
            return mid
        # 元素小于中间位置的元素，只需要再比较左边的元素
        elif arr[mid] > x:
            return binarySearch(arr, l, mid-1, x)
        # 元素大于中间位置的元素，只需要再比较右边的元素
        else:
            return binarySearch(arr, mid+1, r, x)
    else:
        # 不存在
        return -1
 
# 测试数组
arr = [ 2, 3, 4, 10, 40]
x = int(input(&#39;请输入元素：&#39;))
# 函数调用
result = binarySearch(arr, 0, len(arr)-1, x)
 
if result != -1:
    print("元素在数组中的索引为 %d" % result)
else:
    print("元素不在数组中")

Copier après la connexion

Résultat de l'exécution :

Veuillez saisir l'élément : 4
L'index de l'élément dans le tableau est 2

Veuillez saisir l'élément : 5
L'élément n'est pas dans le tableau

Recherche linéaire

Recherche linéaire : fait référence à la vérification de chaque élément du tableau dans un certain ordre jusqu'à ce que la valeur spécifique que vous recherchez soit trouvée.

def search(arr, n, x):
    for i in range (0, n):
        if (arr[i] == x):
            return i
    return -1
 
# 在数组 arr 中查找字符 D
arr = [ &#39;A&#39;, &#39;B&#39;, &#39;C&#39;, &#39;D&#39;, &#39;E&#39; ]
x = input("请输入要查找的元素：")
n = len(arr)
result = search(arr, n, x)
if(result == -1):
    print("元素不在数组中")
else:
    print("元素在数组中的索引为", result)

Copier après la connexion

Résultats d'exécution :

Veuillez saisir l'élément que vous recherchez : A
L'index de l'élément dans le tableau est 0

Veuillez saisir l'élément que vous recherchez : a
L'élément est pas dans le tableau

Tri

Tri par insertion

Tri par insertion : C'est un algorithme de tri simple et intuitif. Il fonctionne en construisant une séquence ordonnée pour les données non triées, il parcourt la séquence triée d'avant en arrière, trouve la position correspondante et l'insère.

Analyse de code dexemple dalgorithme de recherche et de tri Python

def insertionSort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i-1
        while j >= 0 and key < arr[j]:
                arr[j+1] = arr[j]
                j -= 1
        arr[j+1] = key
 
arr = [12, 11, 13, 5, 6, 7, 9, 9, 17]
insertionSort(arr)
print("排序后的数组:")
print(arr)

Copier après la connexion

Résultat d'exécution :

tableau trié :
[5, 6, 7, 9, 9, 11, 12, 13, 17]

Bien sûr, cela peut aussi être écrit comme ceci, ce qui est plus concis

list1 = [12, 11, 13, 5, 6, 7, 9, 9, 17]
for i in range(len(list1)-1, 0, -1):
    for j in range(0, i):
        if list1[i] < list1[j]:
            list1[i], list1[j] = list1[j], list1[i]
print(list1)

Copier après la connexion

Tri rapide

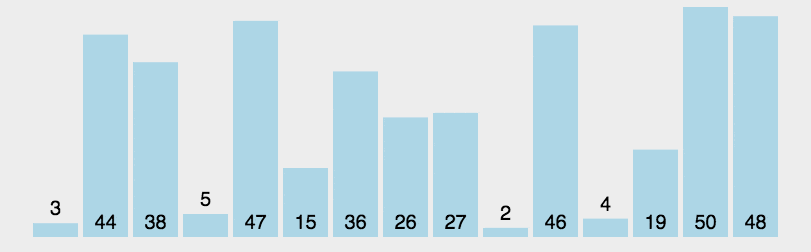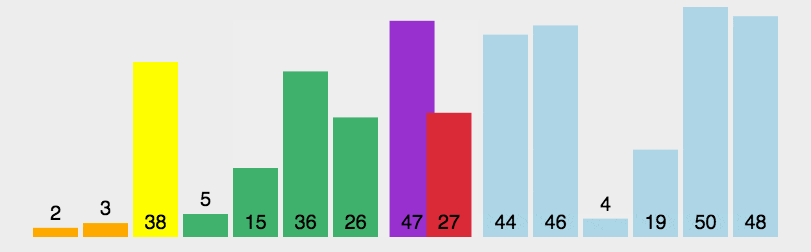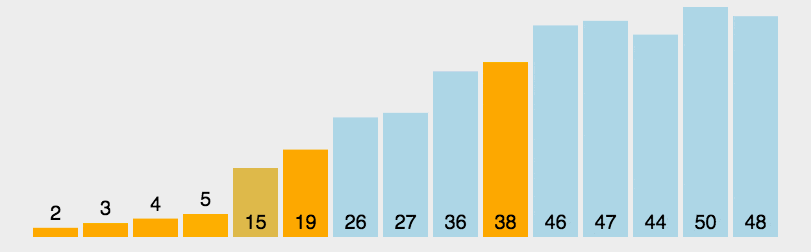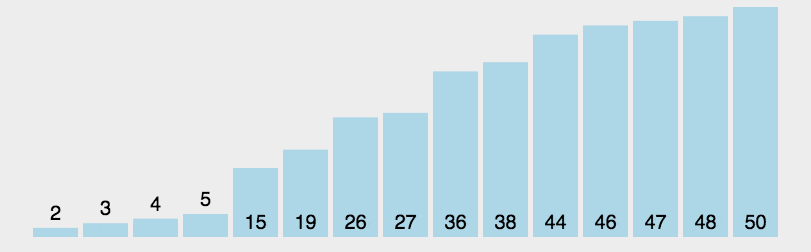
Tri rapide ;Utilisez la stratégie diviser pour régner pour diviser une séquence (liste) en deux sous-séquences, une plus petite et une plus grande, puis trier les deux sous-séquences de manière récursive.

Les étapes sont les suivantes :

Choisissez la valeur pivot : Sélectionnez un élément de la séquence, appelé "pivot" (pivot)
Split : Réorganisez la séquence pour que tout les valeurs sont inférieures à la valeur pivot. Les petits éléments sont placés devant le pivot, et tous les éléments plus grands que la valeur pivot sont placés derrière le pivot (les nombres égaux à la valeur pivot peuvent aller de chaque côté). Une fois cette division terminée, le tri de la valeur de référence est terminé ;
Trier récursivement les sous-séquences : Trier récursivement les sous-séquences d'éléments plus petites que la valeur de référence et les sous-séquences d'éléments supérieures à la valeur de référence.

La condition de jugement pour récurer vers le bas est que la taille de la séquence est zéro ou un. À ce moment, la séquence est évidemment en ordre.

Il existe plusieurs méthodes spécifiques de sélection de la valeur de référence. Cette méthode de sélection a un impact déterminant sur les performances temporelles du tri.

Analyse de code dexemple dalgorithme de recherche et de tri Python

def partition(arr, low, high):
    i = (low-1)         # 最小元素索引
    pivot = arr[high]
 
    for j in range(low, high):
        # 当前元素小于或等于 pivot
        if arr[j] <= pivot:
            i = i+1
            arr[i], arr[j] = arr[j], arr[i]
 
    arr[i+1], arr[high] = arr[high], arr[i+1]
    return (i+1)
 
# arr[] --> 排序数组
# low  --> 起始索引
# high  --> 结束索引
 
# 快速排序函数
def quickSort(arr, low, high):
    if low < high:
        pi = partition(arr, low, high)
        quickSort(arr, low, pi-1)
        quickSort(arr, pi+1, high)
    return arr
 
arr = [10, 7, 8, 9, 1, 5]
n = len(arr)
 
print("排序后的数组:")
print(quickSort(arr, 0, n-1))

Copier après la connexion

Résultats en cours:

Analyse de code dexemple dalgorithme de recherche et de tri Python

Red Sorted Tableau: [1, 5, 7, 8, 9, 10] . Voici comment cela fonctionne.

Trouvez d'abord le plus petit (grand) élément de la séquence non triée et stockez-le au début de la séquence triée. Ensuite, continuez à trouver le plus petit (grand) élément parmi les éléments non triés restants et placez-le à la fin de la séquence triée. séquence. Et ainsi de suite jusqu'à ce que tous les éléments soient triés.

A = [64, 25, 12, 22, 11]
for i in range(len(A)): 
    min_idx = i
    for j in range(i+1, len(A)):
        if A[min_idx] > A[j]:
            min_idx = j
 
    A[i], A[min_idx] = A[min_idx], A[i]
 
print("排序后的数组：")
print(A)

Copier après la connexion

Résultat d'exécution :

tableau trié :

[11, 12, 22, 25, 64]

Analyse de code dexemple dalgorithme de recherche et de tri Python

Tri à bulles

Tri à bulles :

Également un outil simple et intuitif algorithme de tri. Il parcourt à plusieurs reprises la séquence à trier, en comparant deux éléments à la fois et en les échangeant s'ils sont dans le mauvais ordre. Le travail de visite du tableau est répété jusqu'à ce qu'aucun échange ne soit plus nécessaire, ce qui signifie que le tableau a été trié. Le nom de cet algorithme vient du fait que les éléments plus petits « flotteront » lentement vers le haut du tableau grâce à l’échange.

def bubbleSort(arr):
    n = len(arr)
    # 遍历所有数组元素
    for i in range(n):
        # Last i elements are already in place
        for j in range(0, n-i-1):
 
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]
    return arr
 
arr = [64, 34, 25, 12, 22, 11, 90]
 
print("排序后的数组:")
print(bubbleSort(arr))

Copier après la connexion

🎜🎜Résultat de l'exécution : 🎜 🎜🎜🎜tableau trié :🎜[11, 12, 22, 25, 34, 64, 90]🎜

归并排序

归并排序（Merge sort，或mergesort）：，是创建在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

分治法:

分割：递归地把当前序列平均分割成两半。
集成：在保持元素顺序的同时将上一步得到的子序列集成到一起（归并）。

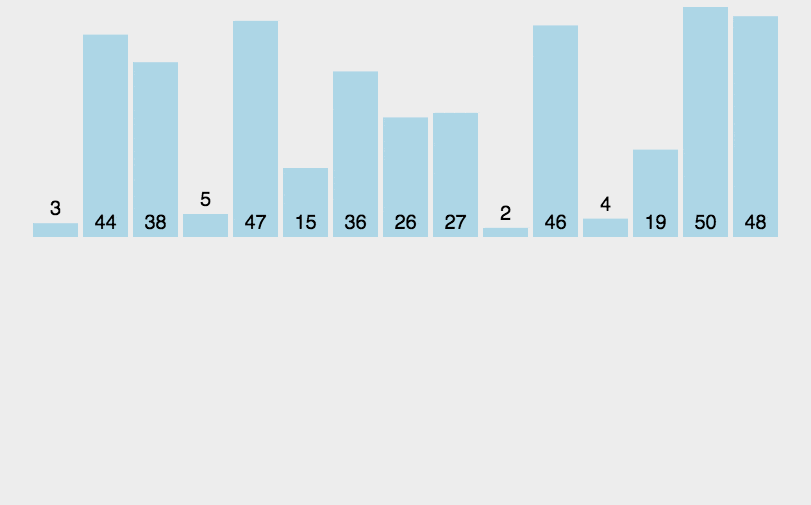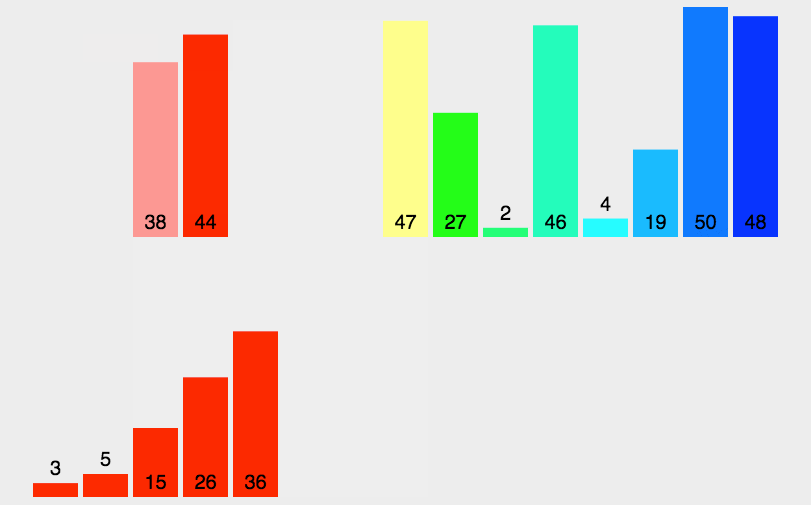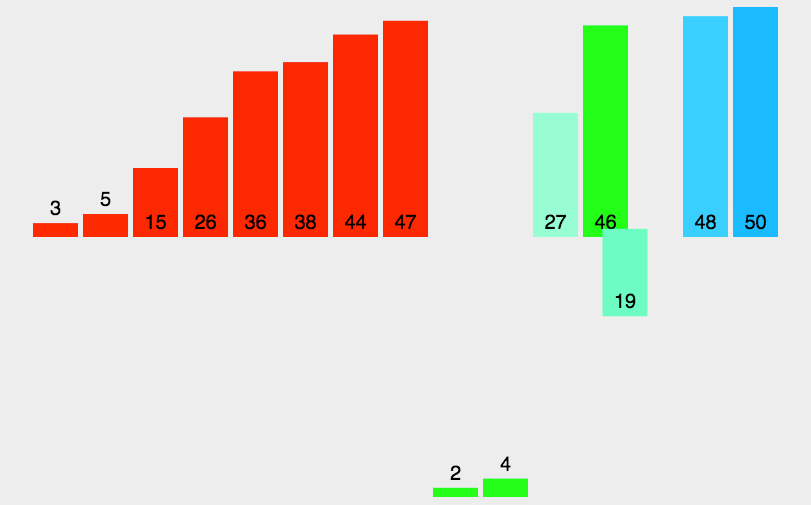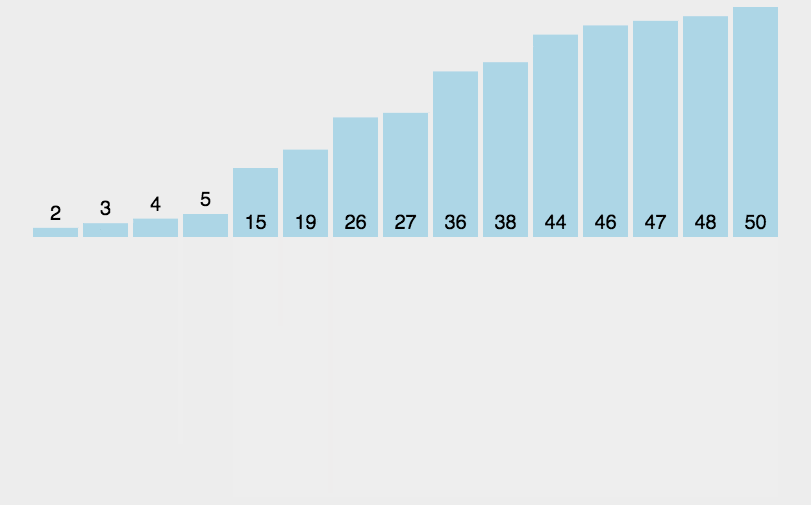
Analyse de code dexemple dalgorithme de recherche et de tri Python

def merge(arr, l, m, r):
    n1 = m - l + 1
    n2 = r - m
 
    # 创建临时数组
    L = [0] * (n1)
    R = [0] * (n2)
 
    # 拷贝数据到临时数组 arrays L[] 和 R[]
    for i in range(0, n1):
        L[i] = arr[l + i]
 
    for j in range(0, n2):
        R[j] = arr[m + 1 + j]
 
    # 归并临时数组到 arr[l..r]
    i = 0     # 初始化第一个子数组的索引
    j = 0     # 初始化第二个子数组的索引
    k = l     # 初始归并子数组的索引
 
    while i < n1 and j < n2:
        if L[i] <= R[j]:
            arr[k] = L[i]
            i += 1
        else:
            arr[k] = R[j]
            j += 1
        k += 1
 
    # 拷贝 L[] 的保留元素
    while i < n1:
        arr[k] = L[i]
        i += 1
        k += 1
 
    # 拷贝 R[] 的保留元素
    while j < n2:
        arr[k] = R[j]
        j += 1
        k += 1
 
def mergeSort(arr, l, r):
    if l < r:
        m = int((l+(r-1))/2)
        mergeSort(arr, l, m)
        mergeSort(arr, m+1, r)
        merge(arr, l, m, r)
    return arr
 
print ("给定的数组")
arr = [12, 11, 13, 5, 6, 7, 13]
print(arr)
n = len(arr)
mergeSort(arr, 0, n-1)
print("排序后的数组")
print(arr)

Copier après la connexion

运行结果：

给定的数组
[12, 11, 13, 5, 6, 7, 13]
排序后的数组
[5, 6, 7, 11, 12, 13, 13]

堆排序

堆排序（Heapsort）：是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。

Analyse de code dexemple dalgorithme de recherche et de tri Python

def heapify(arr, n, i):
    largest = i
    l = 2 * i + 1     # left = 2*i + 1
    r = 2 * i + 2     # right = 2*i + 2
    if l < n and arr[i] < arr[l]:
        largest = l
    if r < n and arr[largest] < arr[r]:
        largest = r
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]  # 交换
def heapSort(arr):
    n = len(arr)
    # Build a maxheap.
    for i in range(n, -1, -1):
        heapify(arr, n, i)
    # 一个个交换元素
    for i in range(n-1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]   # 交换
        heapify(arr, i, 0)
    return arr
arr = [12, 11, 13, 5, 6, 7, 13, 18]
heapSort(arr)
print("排序后的数组")
print(heapSort(arr))

Copier après la connexion

运行结果：

排序后的数组
[5, 6, 7, 12, 11, 13, 13, 18]

计数排序

计数排序：的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

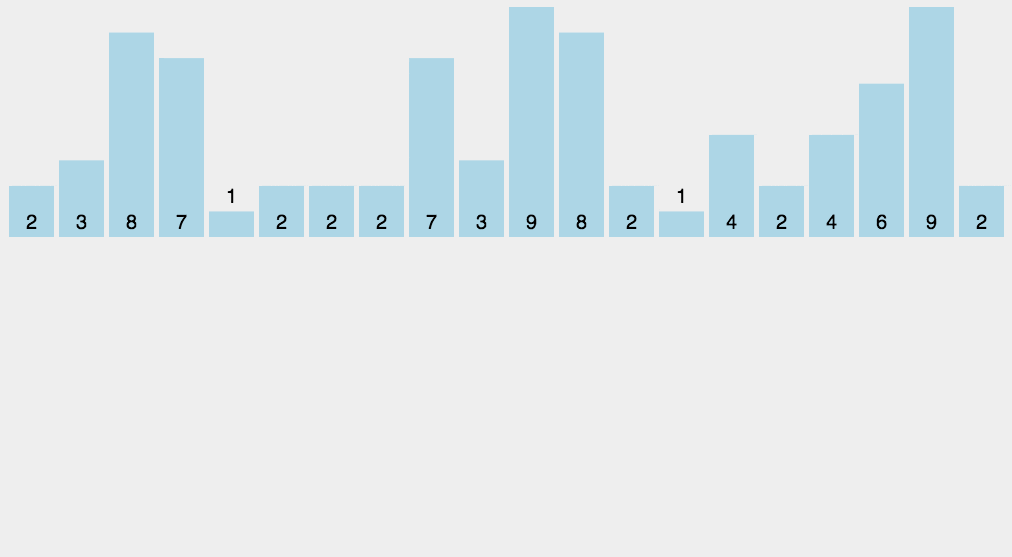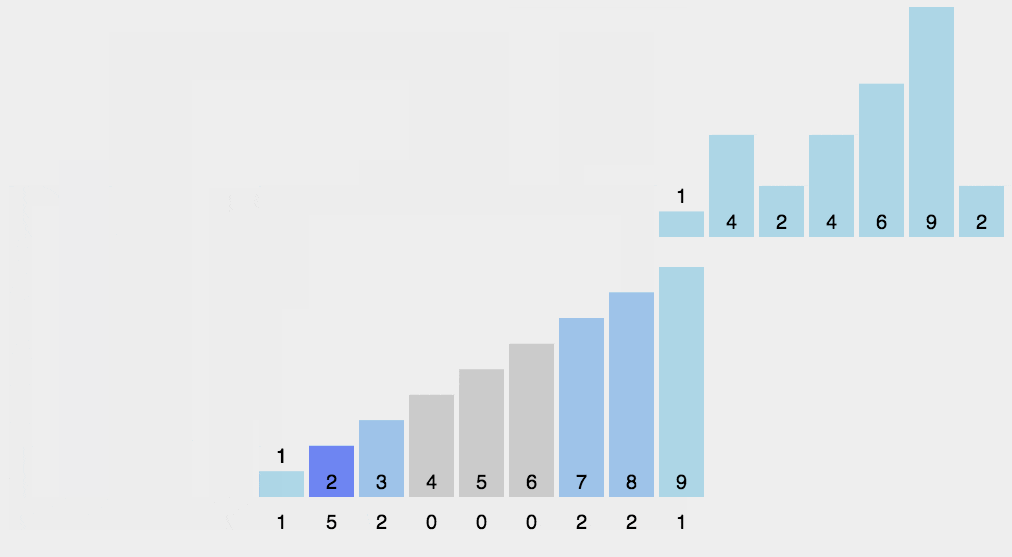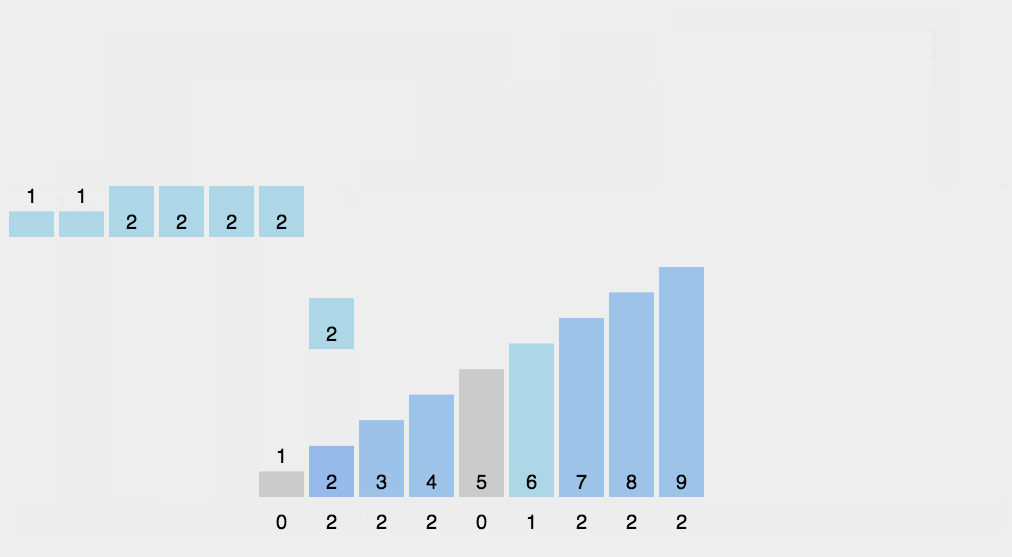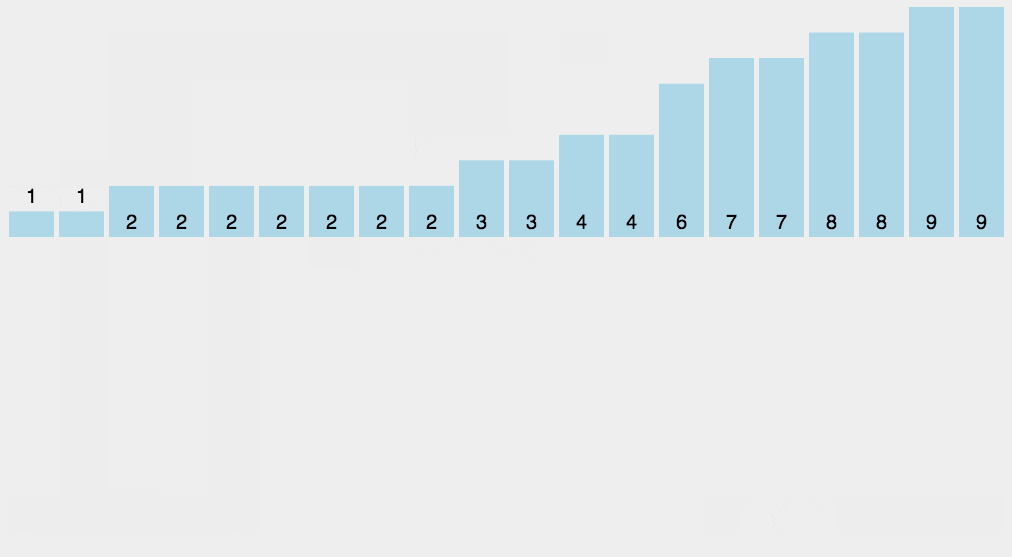
Analyse de code dexemple dalgorithme de recherche et de tri Python

def countSort(arr):
    output = [0 for i in range(256)]
    count = [0 for i in range(256)]
    ans = ["" for _ in arr]
    for i in arr:
        count[ord(i)] += 1
    for i in range(256):
        count[i] += count[i-1] 
    for i in range(len(arr)):
        output[count[ord(arr[i])]-1] = arr[i]
        count[ord(arr[i])] -= 1
    for i in range(len(arr)):
        ans[i] = output[i]
    return ans
arr = "wwwnowcodercom"
ans = countSort(arr)
print("字符数组排序 %s" %("".join(ans)))

Copier après la connexion

运行结果：

字符数组排序 ccdemnooorwwww

希尔排序

希尔排序：也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。

希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行依次直接插入排序。

Analyse de code dexemple dalgorithme de recherche et de tri Python

def shellSort(arr):
    n = len(arr)
    gap = int(n/2)
 
    while gap > 0:
        for i in range(gap, n):
            temp = arr[i]
            j = i
            while j >= gap and arr[j-gap] > temp:
                arr[j] = arr[j-gap]
                j -= gap
            arr[j] = temp
        gap = int(gap/2)
    return arr
 
arr = [12, 34, 54, 2, 3, 2, 5]
 
print("排序前:")
print(arr)
print("排序后:")
print(shellSort(arr))

Copier après la connexion

运行结果：

排序前:
[12, 34, 54, 2, 3, 2, 5]
排序后:
[2, 2, 3, 5, 12, 34, 54]

拓扑排序

对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边(u,v)∈E(G)，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。拓扑排序是一种将集合上的偏序转换为全序的操作。

在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序（英语：Topological sorting）：

每个顶点出现且只出现一次；若A在序列中排在B的前面，则在图中不存在从B到A的路径。

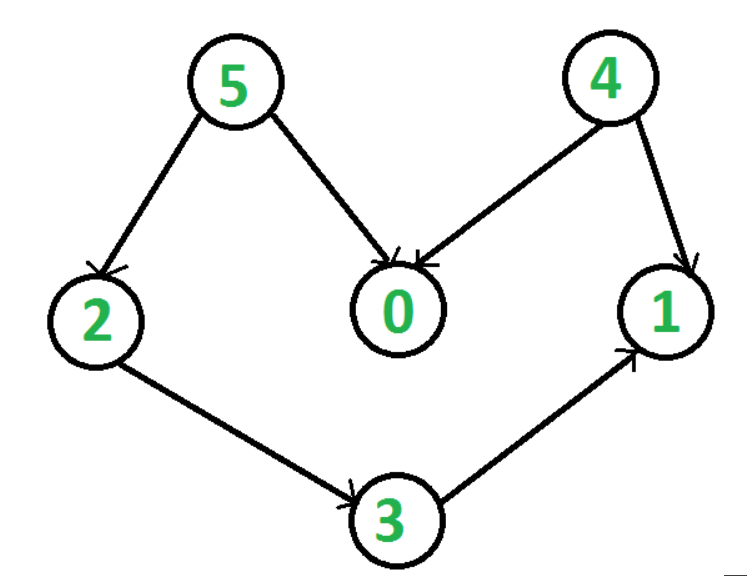
Analyse de code dexemple dalgorithme de recherche et de tri Python

from collections import defaultdict
class Graph:
    def __init__(self, vertices):
        self.graph = defaultdict(list)
        self.V = vertices
    def addEdge(self, u, v):
        self.graph[u].append(v)
    def topologicalSortUtil(self, v, visited, stack):
 
        visited[v] = True
 
        for i in self.graph[v]:
            if visited[i] == False:
                self.topologicalSortUtil(i, visited, stack)
        stack.insert(0,v)
    def topologicalSort(self):
        visited = [False]*self.V
        stack = []
        for i in range(self.V):
            if visited[i] == False:
                self.topologicalSortUtil(i, visited, stack)
        print(stack)
g= Graph(6)
g.addEdge(5, 2)
g.addEdge(5, 0)
g.addEdge(4, 0)
g.addEdge(4, 1)
g.addEdge(2, 3)
g.addEdge(3, 1)
print("拓扑排序结果：")
g.topologicalSort()

Copier après la connexion

运行结果：