Comment implémenter le tri par sélection de l'algorithme de tri Python

1. Introduction

L'algorithme de tri primaire fait référence à plusieurs algorithmes de tri basiques et faciles à comprendre. Il existe trois algorithmes de tri principaux : le tri par insertion, le tri par sélection et le tri par bulles. Bien que leur efficacité soit inférieure à celle des algorithmes de tri avancés, après avoir compris l'algorithme de tri principal, il sera beaucoup plus facile d'apprendre l'algorithme de tri avancé relativement complexe.

2. Description

Le tri par sélection consiste à sélectionner à chaque fois la plus petite ou la plus grande donnée d'un tableau non ordonné et à la placer du tableau non ordonné à la fin du tableau ordonné, pour obtenir l'effet de tri.

La complexité temporelle moyenne du tri par sélection est O(n2), et la complexité temporelle dans le meilleur des cas et la complexité temporelle dans le pire des cas sont toutes deux O(n2). De plus, il s'agit d'un algorithme de tri instable. Le processus de tri par sélection est facile à comprendre. En prenant l'algorithme de tri ascendant comme exemple, nous parcourons d'abord le tableau non trié et trouvons le plus petit élément, comme le montre la figure 2-4. Ensuite, supprimez le plus petit élément du tableau non trié et ajoutez-le à la fin du tableau trié.

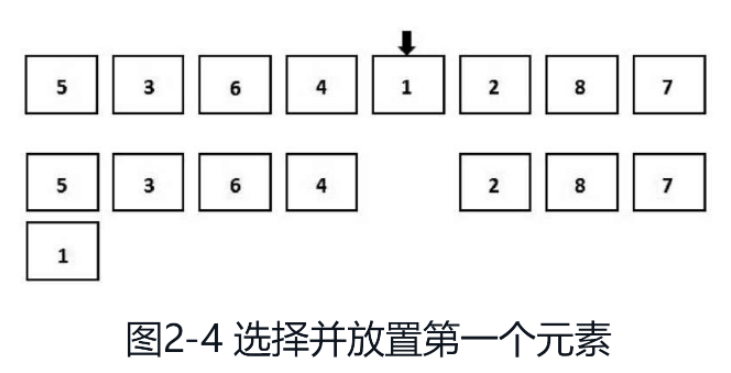
Parce que le plus petit élément est 1, 1 est ajouté à la fin du tableau ordonné qui est encore vide.

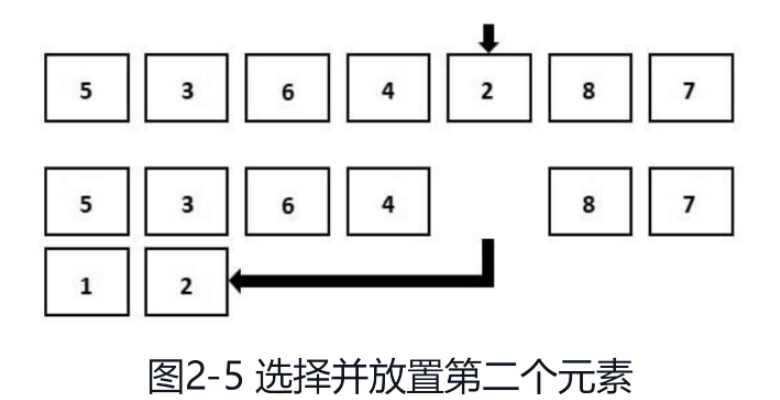
Comme le montre la figure 2-5, nous continuons à parcourir les éléments restants. Cette fois, le plus petit élément est 2. Nous l'ajoutons à la fin du tableau trié. Cette opération est correcte car les éléments du tableau trié doivent être plus petits que les éléments du tableau non trié.

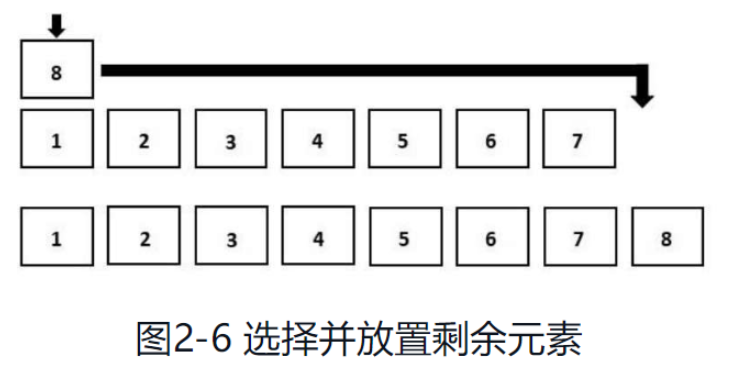
Comme le montre la figure 2-6, répétez les étapes ci-dessus lorsqu'il ne reste qu'un seul élément dans le tableau non trié, ajoutez-le au trié. array À la fin du tableau, le tri de l'ensemble du tableau est terminé.

3. Implémentation du code

Sélectionnez le code de tri :

nums = [5,3,6,4,1,2,8,7]
res = []　　　#用于存储已排序元素的数组
while len(nums): #当未排序数组内还有元素时，重复执行选择最小数的代码
 minInd = 0 #初始化存储最小数下标的变量，默认为第一个数
 for i in range(1, len(nums)):
  if(nums[i] < nums[minInd]): #更新最小数的下标
    minInd = i
 temp = nums[minInd]
 nums.pop(minInd) #把最小数从未排序数组中删除
 res.append(temp) #把最小数插入到已排序数组的末尾
print(res)

Exécutez le programme et sortez les résultats Pour :

[1,2,3,4,5,6,7,8]

Dans le programme, i dans la première boucle for représente la première position du tableau non trié, c'est-à-dire la première position après le tableau ordonné. Ensuite, utilisez une boucle for pour trouver l'indice de la valeur minimale dans le tableau non trié. Initialement, l'index minimum minInd se voit attribuer l'index du premier élément du tableau non trié. Lorsqu'un élément plus petit que le minimum actuel est rencontré, mettez simplement à jour l'index et parcourez l'ensemble du tableau. Après avoir échangé la valeur minimale trouvée avec le premier élément du tableau non trié, la valeur minimale est placée à la fin du tableau ordonné.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!