 développement back-end
développement back-end
 Tutoriel Python
Tutoriel Python
 Stratégies de trading et analyse de portefeuille avec Python
Stratégies de trading et analyse de portefeuille avec Python
Stratégies de trading et analyse de portefeuille avec Python
Nous mesurerons les performances des stratégies de trading dans cet article. Et développera une stratégie de trading dynamique simple qui utilisera quatre classes d'actifs : obligations, actions et immobilier. Ces classes d’actifs ont de faibles corrélations, ce qui en fait d’excellentes options d’équilibrage des risques.

Momentum Trading Strategy
Cette stratégie est basée sur le momentum car les traders et les investisseurs sont depuis longtemps conscients du momentum. L'impact peut être visible sur un large éventail de marchés et de périodes. Nous appelons donc cela une stratégie dynamique. Le suivi de tendance ou l'élan des séries chronologiques (TSM) est un autre nom pour l'utilisation de ces stratégies sur un seul instrument. Nous allons créer une stratégie de dynamique de base et la tester sur TCS pour voir comment elle fonctionne.
Analyse de stratégie TSM
Tout d'abord, nous allons importer quelques bibliothèques
import numpy as np import pandas as pd import matplotlib.pyplot as plt import yfinance as yf import ffn %matplotlib inline
Nous construisons la fonction de stratégie de dynamique de base TSMStrategy. La fonction renverra les performances attendues via le retour logarithmique de la série chronologique, la période d'intérêt et une variable booléenne indiquant si la vente à découvert est autorisée.
def TSMStrategy(returns, period=1, shorts=False):
if shorts:
position = returns.rolling(period).mean().map(
lambda x: -1 if x <= 0 else 1)
else:
position = returns.rolling(period).mean().map(
lambda x: 0 if x <= 0 else 1)
performance = position.shift(1) * returns
return performance
ticker = 'TCS'
yftcs = yf.Ticker(ticker)
data = yftcs.history(start='2005-01-01', end='2021-12-31')
returns = np.log(data['Close'] / data['Close'].shift(1)).dropna()
performance = TSMStrategy(returns, period=1, shorts=False).dropna()
years = (performance.index.max() - performance.index.min()).days / 365
perf_cum = np.exp(performance.cumsum())
tot = perf_cum[-1] - 1
ann = perf_cum[-1] ** (1 / years) - 1
vol = performance.std() * np.sqrt(252)
rfr = 0.02
sharpe = (ann - rfr) / vol
print(f"1-day TSM Strategy yields:" +
f"nt{tot*100:.2f}% total returns" +
f"nt{ann*100:.2f}% annual returns" +
f"nt{sharpe:.2f} Sharpe Ratio")
tcs_ret = np.exp(returns.cumsum())
b_tot = tcs_ret[-1] - 1
b_ann = tcs_ret[-1] ** (1 / years) - 1
b_vol = returns.std() * np.sqrt(252)
b_sharpe = (b_ann - rfr) / b_vol
print(f"Baseline Buy-and-Hold Strategy yields:" +
f"nt{b_tot*100:.2f}% total returns" +
f"nt{b_ann*100:.2f}% annual returns" +
f"nt{b_sharpe:.2f} Sharpe Ratio")Le résultat de la fonction est le suivant :
1-day TSM Strategy yields: -45.15% total returns -7.10% annual returns -0.17 Sharpe Ratio Baseline Buy-and-Hold Strategy yields: -70.15% total returns -13.78% annual returns -0.22 Sharpe Ratio
En termes de rendements annualisés raisonnables, la stratégie TSM sur 1 jour est meilleure que la stratégie d'achat et de conservation. Étant donné qu’une analyse rétrospective sur un jour peut contenir de nombreuses fausses tendances, nous avons essayé différentes périodes pour voir comment elles se comparent. Ici, le modèle sera exécuté en boucle pendant 3, 5, 15, 30 et 90 jours.
import matplotlib.gridspec as gridspec
periods = [3, 5, 15, 30, 90]
fig = plt.figure(figsize=(12, 10))
gs = fig.add_gridspec(4, 4)
ax0 = fig.add_subplot(gs[:2, :4])
ax1 = fig.add_subplot(gs[2:, :2])
ax2 = fig.add_subplot(gs[2:, 2:])
ax0.plot((np.exp(returns.cumsum()) - 1) * 100, label=ticker, linestyle='-')
perf_dict = {'tot_ret': {'buy_and_hold': (np.exp(returns.sum()) - 1)}}
perf_dict['ann_ret'] = {'buy_and_hold': b_ann}
perf_dict['sharpe'] = {'buy_and_hold': b_sharpe}
for p in periods:
log_perf = TSMStrategy(returns, period=p, shorts=False)
perf = np.exp(log_perf.cumsum())
perf_dict['tot_ret'][p] = (perf[-1] - 1)
ann = (perf[-1] ** (1/years) - 1)
perf_dict['ann_ret'][p] = ann
vol = log_perf.std() * np.sqrt(252)
perf_dict['sharpe'][p] = (ann - rfr) / vol
ax0.plot((perf - 1) * 100, label=f'{p}-Day Mean')
ax0.set_ylabel('Returns (%)')
ax0.set_xlabel('Date')
ax0.set_title('Cumulative Returns')
ax0.grid()
ax0.legend()
_ = [ax1.bar(i, v * 100) for i, v in enumerate(perf_dict['ann_ret'].values())]
ax1.set_xticks([i for i, k in enumerate(perf_dict['ann_ret'])])
ax1.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['ann_ret'].keys()],
rotation=45)
ax1.grid()
ax1.set_ylabel('Returns (%)')
ax1.set_xlabel('Strategy')
ax1.set_title('Annual Returns')
_ = [ax2.bar(i, v) for i, v in enumerate(perf_dict['sharpe'].values())]
ax2.set_xticks([i for i, k in enumerate(perf_dict['sharpe'])])
ax2.set_xticklabels([f'{k}-Day Mean'
if type(k) is int else ticker for
k in perf_dict['sharpe'].keys()],
rotation=45)
ax2.grid()
ax2.set_ylabel('Sharpe Ratio')
ax2.set_xlabel('Strategy')
ax2.set_title('Sharpe Ratio')
plt.tight_layout()
plt.show()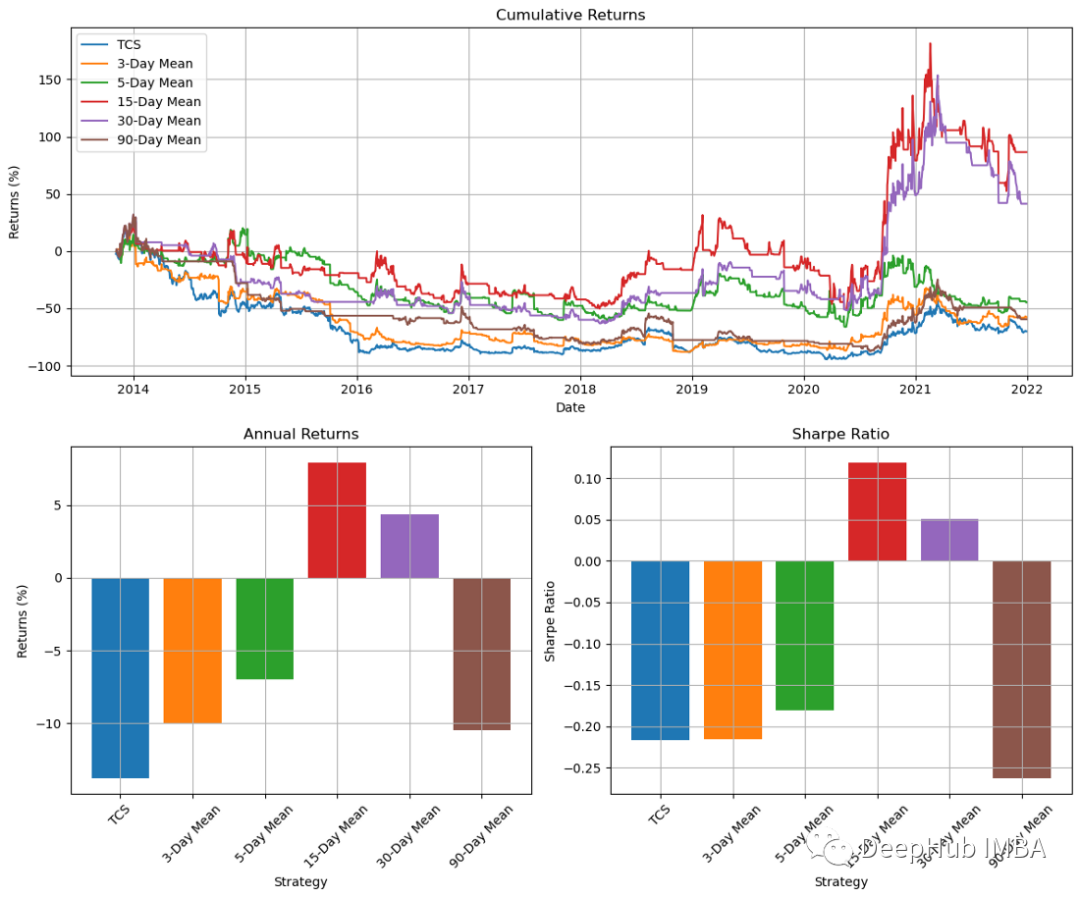
En regardant les résultats sur le graphique, nous pouvons voir que l'indicateur de momentum sur 15 jours fournit les meilleurs résultats. Toutefois, les résultats pour les autres périodes sont mitigés. Cela montre que notre stratégie n’est pas fiable. Nous pouvons donc également quitter la transaction en utilisant un stop ou un stop suiveur près du sommet, plutôt que de le faire lorsque le graphique sur 15 jours est en baisse ou à plat.
PORTfolio Analysis
Jusqu'à présent, nous avons créé une stratégie de trading en Python. Ci-dessous, nous mesurerons et tracerons les caractéristiques communes du portefeuille pour faciliter notre observation et notre analyse.
PORTfolio Analysis
Tout d'abord, nous allons importer quelques bibliothèques importantes et observer l'exécution des données.
import pandas_datareader.data as web stocks = ['SPY','GLD','TLT','HYG'] data = web.DataReader(stocks,data_source='yahoo',start='01/01/2019')['Adj Close'] data.sort_index(ascending=True,inplace=True) perf = data.calc_stats() perf.plot()
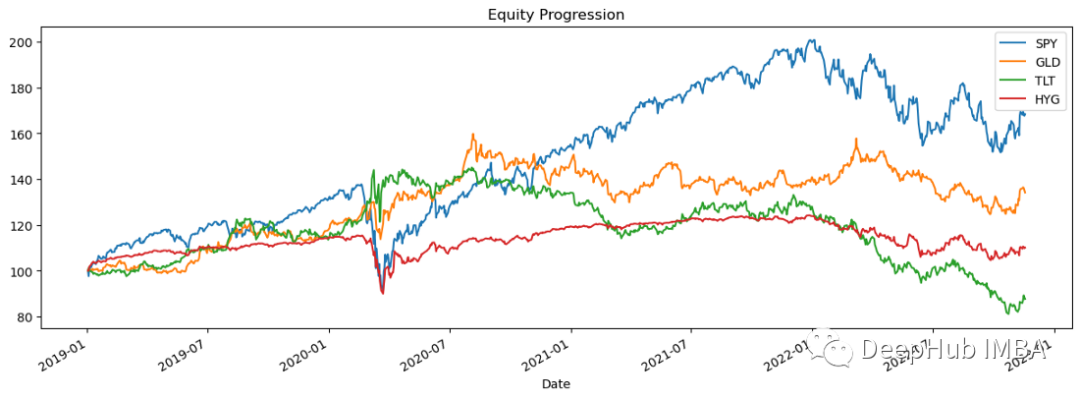
Log return
Le retour du journal est utilisé pour calculer le taux de croissance exponentielle. Au lieu de calculer le pourcentage de variation de prix pour chaque sous-période, nous calculons l'indice de croissance organique pour cette période. Créez d'abord un df qui contient le retour journal de chaque cours d'action dans les données, puis nous créons un histogramme pour chaque retour journal.
returns = data.to_log_returns().dropna() print(returns.head()) Symbols SPY GLD TLT HYG Date 2019-01-03 -0.024152 0.009025 0.011315 0.000494 2019-01-04 0.032947 -0.008119 -0.011642 0.016644 2019-01-07 0.007854 0.003453 -0.002953 0.009663 2019-01-08 0.009351 -0.002712 -0.002631 0.006470 2019-01-09 0.004663 0.006398 -0.001566 0.001193
L'histogramme est le suivant :
ax = returns.hist(figsize=(20, 10),bins=30)
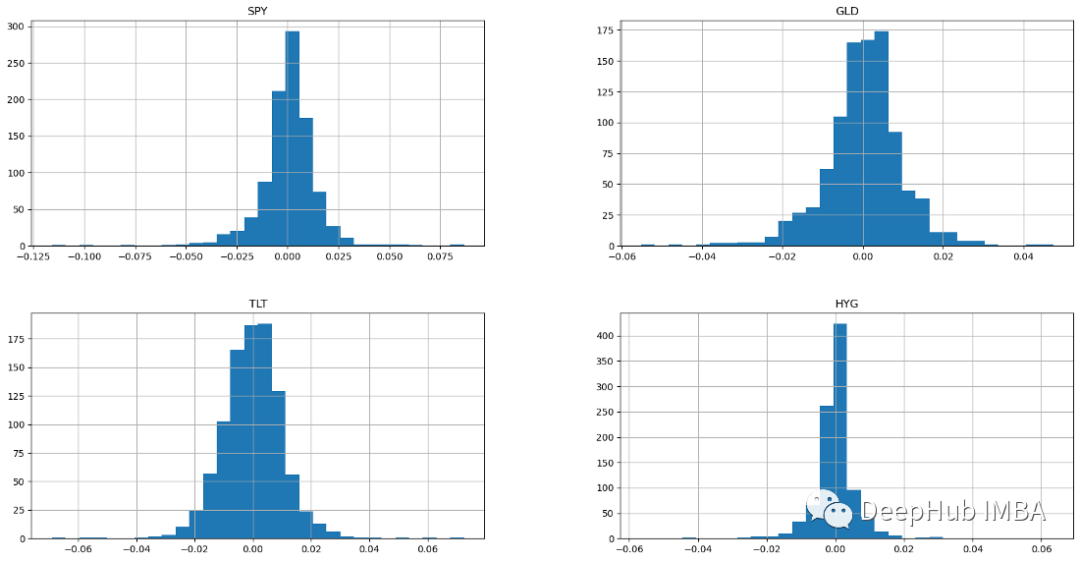
Histogramme montrant la distribution normale pour les quatre classes d'actifs. Un échantillon avec une distribution normale a une moyenne arithmétique et une distribution égale au-dessus et au-dessous de la moyenne (la distribution normale également connue sous le nom de distribution gaussienne est symétrique). Si les rendements sont normalement distribués, plus de 99 % des rendements devraient se situer dans une fourchette de trois écarts types par rapport à la moyenne. Ces caractéristiques de distribution normale en forme de cloche permettent aux analystes et aux investisseurs de faire de meilleures déductions statistiques sur les rendements et les risques attendus d'une action. Les actions avec une courbe en cloche sont généralement des valeurs sûres avec une volatilité faible et prévisible.
Taux de retracement maximum DRAWDOWN
DRAWDOWN fait référence à la valeur tombant à un niveau relativement bas. Il s’agit d’un facteur de risque important à prendre en compte par les investisseurs. Dessinons une représentation visuelle de la stratégie décroissante.
ffn.to_drawdown_series(data).plot(figsize=(15,10))
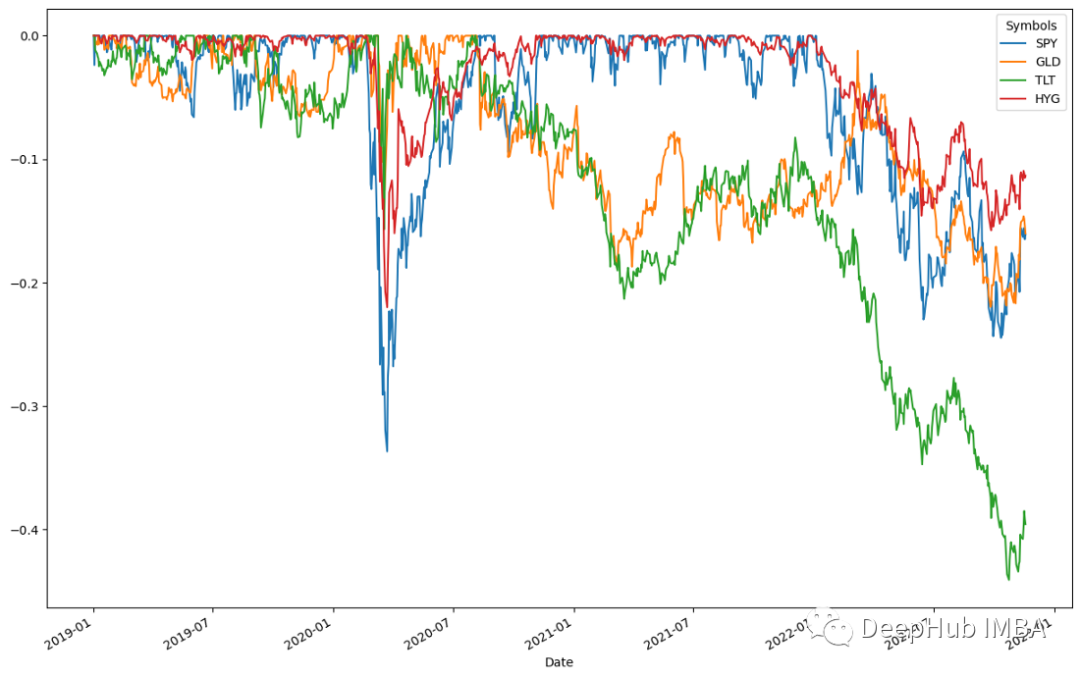
Les quatre actifs ont diminué au premier semestre 2020, SPY ayant enregistré la plus forte baisse de 0,5 %. Puis, au premier semestre 2020, tous les actifs se sont immédiatement redressés. Cela indique un taux élevé de récupération des actifs. Ces actifs ont culminé vers juillet 2020. Suivant cette tendance, toutes les classes d’actifs ont connu de légères baisses une fois la reprise attelée. Selon les résultats, le TLT connaîtra la plus forte baisse de 0,5 % au second semestre 2022 avant de se redresser début 2023.
MARKOWITZ Optimisation moyenne-variance
En 1952, Markowitz (MARKOWITZ) a proposé la théorie du portefeuille moyenne-variance, également connue sous le nom de théorie moderne du portefeuille. Les investisseurs peuvent utiliser ces concepts pour construire un portefeuille qui maximise les rendements attendus en fonction d'un niveau de risque donné. Grâce à la méthode de Markowitz, nous pouvons générer un « portefeuille optimal ».
returns.calc_mean_var_weights().as_format('.2%')
#结果
SPY 46.60%
GLD 53.40%
TLT 0.00%
HYG 0.00%
dtype: objectStatistiques de corrélation
La corrélation est une méthode statistique utilisée pour mesurer la relation entre les titres. Ces informations sont mieux visualisées à l’aide de cartes thermiques. Les Heatmaps nous permettent de voir les corrélations entre les titres.
returns.plot_corr_heatmap()
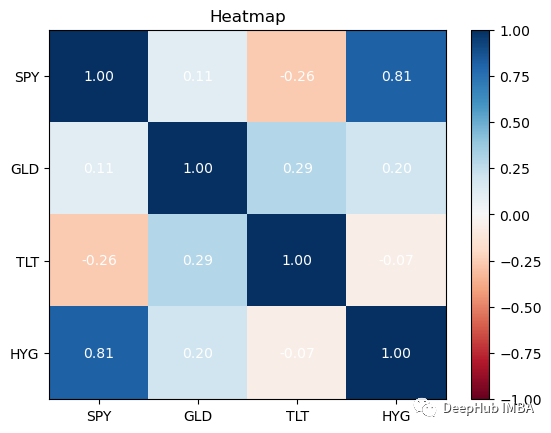
最好在你的投资组合中拥有相关性较低的资产。除了SPY与HYG,这四个资产类别的相关性都很低,这对我们的投资组合是不利的:因为如果拥有高度相关的不同资产组,即使你将风险分散在它们之间,从投资组合构建的角度来看,收益也会很少。
总结
通过分析和绘制的所有数据进行资产配置,可以建立一个投资组合,极大地改变基础投资的风险特征。还有很多我没有提到的,但可以帮助我们确定交易策略价值的起点。我们将在后续文章中添加更多的技术性能指标。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 PHP et Python: exemples de code et comparaison
Apr 15, 2025 am 12:07 AM
PHP et Python: exemples de code et comparaison
Apr 15, 2025 am 12:07 AM
PHP et Python ont leurs propres avantages et inconvénients, et le choix dépend des besoins du projet et des préférences personnelles. 1.Php convient au développement rapide et à la maintenance des applications Web à grande échelle. 2. Python domine le domaine de la science des données et de l'apprentissage automatique.
 Python vs JavaScript: communauté, bibliothèques et ressources
Apr 15, 2025 am 12:16 AM
Python vs JavaScript: communauté, bibliothèques et ressources
Apr 15, 2025 am 12:16 AM
Python et JavaScript ont leurs propres avantages et inconvénients en termes de communauté, de bibliothèques et de ressources. 1) La communauté Python est amicale et adaptée aux débutants, mais les ressources de développement frontal ne sont pas aussi riches que JavaScript. 2) Python est puissant dans les bibliothèques de science des données et d'apprentissage automatique, tandis que JavaScript est meilleur dans les bibliothèques et les cadres de développement frontaux. 3) Les deux ont des ressources d'apprentissage riches, mais Python convient pour commencer par des documents officiels, tandis que JavaScript est meilleur avec MDNWEBDOCS. Le choix doit être basé sur les besoins du projet et les intérêts personnels.
 Explication détaillée du principe docker
Apr 14, 2025 pm 11:57 PM
Explication détaillée du principe docker
Apr 14, 2025 pm 11:57 PM
Docker utilise les fonctionnalités du noyau Linux pour fournir un environnement de fonctionnement d'application efficace et isolé. Son principe de travail est le suivant: 1. Le miroir est utilisé comme modèle en lecture seule, qui contient tout ce dont vous avez besoin pour exécuter l'application; 2. Le Système de fichiers Union (UnionFS) empile plusieurs systèmes de fichiers, ne stockant que les différences, l'économie d'espace et l'accélération; 3. Le démon gère les miroirs et les conteneurs, et le client les utilise pour l'interaction; 4. Les espaces de noms et les CGROUP implémentent l'isolement des conteneurs et les limitations de ressources; 5. Modes de réseau multiples prennent en charge l'interconnexion du conteneur. Ce n'est qu'en comprenant ces concepts principaux que vous pouvez mieux utiliser Docker.
 Comment exécuter des programmes dans Terminal Vscode
Apr 15, 2025 pm 06:42 PM
Comment exécuter des programmes dans Terminal Vscode
Apr 15, 2025 pm 06:42 PM
Dans VS Code, vous pouvez exécuter le programme dans le terminal via les étapes suivantes: Préparez le code et ouvrez le terminal intégré pour vous assurer que le répertoire de code est cohérent avec le répertoire de travail du terminal. Sélectionnez la commande Run en fonction du langage de programmation (tel que Python de Python your_file_name.py) pour vérifier s'il s'exécute avec succès et résoudre les erreurs. Utilisez le débogueur pour améliorer l'efficacité du débogage.
 Python: automatisation, script et gestion des tâches
Apr 16, 2025 am 12:14 AM
Python: automatisation, script et gestion des tâches
Apr 16, 2025 am 12:14 AM
Python excelle dans l'automatisation, les scripts et la gestion des tâches. 1) Automatisation: La sauvegarde du fichier est réalisée via des bibliothèques standard telles que le système d'exploitation et la fermeture. 2) Écriture de script: utilisez la bibliothèque PSUTIL pour surveiller les ressources système. 3) Gestion des tâches: utilisez la bibliothèque de planification pour planifier les tâches. La facilité d'utilisation de Python et la prise en charge de la bibliothèque riche en font l'outil préféré dans ces domaines.
 L'extension VScode est-elle malveillante?
Apr 15, 2025 pm 07:57 PM
L'extension VScode est-elle malveillante?
Apr 15, 2025 pm 07:57 PM
Les extensions de code vs posent des risques malveillants, tels que la cachette de code malveillant, l'exploitation des vulnérabilités et la masturbation comme des extensions légitimes. Les méthodes pour identifier les extensions malveillantes comprennent: la vérification des éditeurs, la lecture des commentaires, la vérification du code et l'installation avec prudence. Les mesures de sécurité comprennent également: la sensibilisation à la sécurité, les bonnes habitudes, les mises à jour régulières et les logiciels antivirus.
 Qu'est-ce que VScode pour quoi est VScode?
Apr 15, 2025 pm 06:45 PM
Qu'est-ce que VScode pour quoi est VScode?
Apr 15, 2025 pm 06:45 PM
VS Code est le code Visual Studio Nom complet, qui est un éditeur de code multiplateforme gratuit et open source et un environnement de développement développé par Microsoft. Il prend en charge un large éventail de langages de programmation et fournit une mise en surbrillance de syntaxe, une complétion automatique du code, des extraits de code et des invites intelligentes pour améliorer l'efficacité de développement. Grâce à un écosystème d'extension riche, les utilisateurs peuvent ajouter des extensions à des besoins et des langues spécifiques, tels que les débogueurs, les outils de mise en forme de code et les intégrations GIT. VS Code comprend également un débogueur intuitif qui aide à trouver et à résoudre rapidement les bogues dans votre code.
 Comment installer nginx dans Centos
Apr 14, 2025 pm 08:06 PM
Comment installer nginx dans Centos
Apr 14, 2025 pm 08:06 PM
CENTOS L'installation de Nginx nécessite de suivre les étapes suivantes: Installation de dépendances telles que les outils de développement, le devet PCRE et l'OpenSSL. Téléchargez le package de code source Nginx, dézippez-le et compilez-le et installez-le, et spécifiez le chemin d'installation AS / USR / LOCAL / NGINX. Créez des utilisateurs et des groupes d'utilisateurs de Nginx et définissez les autorisations. Modifiez le fichier de configuration nginx.conf et configurez le port d'écoute et le nom de domaine / adresse IP. Démarrez le service Nginx. Les erreurs communes doivent être prêtées à prêter attention, telles que les problèmes de dépendance, les conflits de port et les erreurs de fichiers de configuration. L'optimisation des performances doit être ajustée en fonction de la situation spécifique, comme l'activation du cache et l'ajustement du nombre de processus de travail.





