
Par exemple, 26 * 15, lorsque nous effectuons des opérations de multiplication, nous le calculons généralement comme ceci, multipliez d'abord 5 par 6 Pour obtenir 30, écrivez 0 et mettez 3 de côté. Puis multipliez 5 par 2 Obtenez <code>10 plus le 3 précédent écrit ci-dessous, obtenez 130 après le calcul 5 Puis calculez 1 ; et multipliez-le par 6 et 2 respectivement. Enregistrez le résultat 26 ci-dessous, puis mettez 130code> et <code>26 (avec désalignement) donnent 390. 26 * 15,在进行乘法操作时,我们一般这样算,先用5乘以6得到30,把0写下把3记在一边,再用5乘以2得到10再加上之前的3写在下面,得到130;计算完5再计算1分别乘以6和2把得到的结果26记在下面,然后把130和26相加(有错位)得到390。

看完了十进制的相乘,再来看下二进制的相乘,基本原理是一样的,也是以十字相乘法为例,计算 5 * 7。
5的二进制为101,7的二进制为111,来看下二进制的十字相乘法。
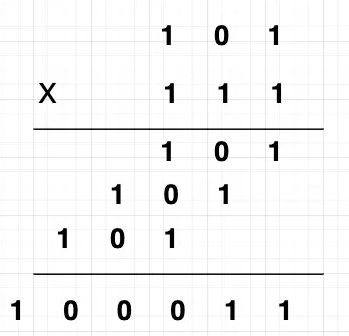
可以看到二进制为101和二进制111用传统的方式来计算,得到的结果为100011,而二进制100011对应的十进制为35。
所以说,在计算的过程中,十进制和二进制的计算方式是一样的,当然这里就不进行举例和证明了。
既然计算过程有了,那么怎么样用代码来实现呢?
我们再来看下上图中二进制的计算过程:
先用二进制111的最后一位1 乘上 101 得到 101。
再用二进制111的倒数第2位1 乘上 101 得到 101。
再用二进制111的倒数第3位1 乘上 101 得到 101。
得到的三个101进行二进制相加,得到 100011。
注意,第2步和第3步得到的结果101都往前挪了一位,相当于1010和10100,也就是最后相加的计算为:10100 + 1010 + 101 = 100011。
再来看得到最终相加的计算10100 + 1010 + 101 = 100011,也就是只要我们找到如何把数据转换为几位数的相加就可以了,因为之前已经实现了如何用位运算实现加法操作。
这三个数101、1010、10100的数量刚好与二进制111的个数相同,也就是二进制(上图下面那个乘数111)有几位就会产生几个数相加,如果是与11111相乘就会产生5个数相加。
再来看数据之前的关系:
第一次相乘结果:101 = 101 + 0
第二次相乘结果:1111 = 101
第三次相乘结果:100011 = 101
从这里我们可以看到,每计算一次,101只需要向左移一次再加上上一次的计算结果就可以了。
那么,怎么知道要左移多少次呢?从这里例子中看,111每次计算后,向右移动一次,101也跟着向左移动一次,直到111
 Binaire multiplication Après avoir lu la multiplication décimale, regardons la multiplication binaire. Le principe de base est le même. Nous prenons également la méthode de multiplication croisée comme exemple pour calculer
Binaire multiplication Après avoir lu la multiplication décimale, regardons la multiplication binaire. Le principe de base est le même. Nous prenons également la méthode de multiplication croisée comme exemple pour calculer 5 * 7. Le système binaire de 5 est 101, et le système binaire de 7 est 111. la loi de multiplication croisée binaire. 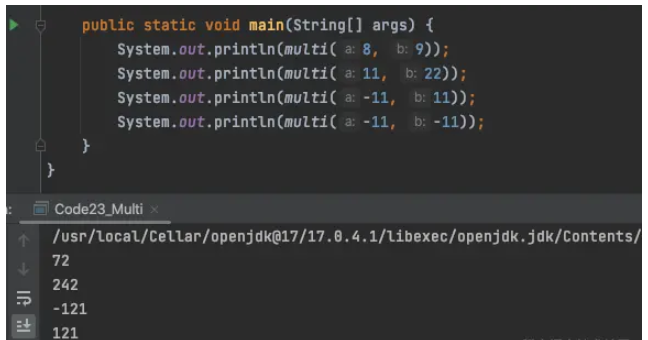

Vous peut voir Le 101 binaire et le 111 binaire sont calculés de la manière traditionnelle, et le résultat est 100011, tandis que le 100011 binaire > La notation décimale correspondante est 35.
Ainsi, dans le processus de calcul, les méthodes de calcul décimal et binaire sont les mêmes. Bien entendu, des exemples et des preuves ne seront pas donnés ici.
1 du binaire <code>111 Multipliez 101 pour obtenir 101. 🎜
1 du binaire 111 par 101 pour obtenir 101code>. 🎜1 du binaire 111 par 101 pour obtenir 101code>. 🎜101 obtenus sont ajoutés en binaire pour obtenir le 100011. 🎜101 obtenus aux étapes 2 et 3 ont été avancés d'un bit, équivalent. à 1010 et 10100, c'est-à-dire que le calcul d'addition final est : 10100 + 1010 + 101 = 100011. 🎜🎜Regardons le calcul de l'addition finale 10100 + 1010 + 101 = 100011, c'est-à-dire que tant que l'on trouve comment convertir les données en addition de plusieurs chiffres, cela suffit, car il a été implémenté auparavant. Comment implémenter une opération d'addition à l'aide d'opérations au niveau du bit. 🎜🎜Les nombres de ces trois nombres 101, 1010 et 10100 sont exactement les mêmes que le nombre du binaire 111 code> C'est-à-dire que le nombre de nombres binaires (le multiplicateur <code>111 en bas de l'image ci-dessus) produira plusieurs nombres une fois ajouté s'il est multiplié par 11111code>, il produira <code> 5les nombres sont additionnés. 🎜🎜Regardons la relation avant les données : 🎜101 = 101 + 0🎜1111 = 101 🎜
100011 = 101 🎜
101 n'a besoin que d'aller vers la gauche. Il suffit de le déplacer une fois et ajoutez le dernier résultat du calcul. 🎜🎜Alors, comment savoir combien de fois il faut décaler vers la gauche ? Dans l'exemple ici, 111 se déplace vers la droite une fois après chaque calcul, et 101 se déplace également une fois vers la gauche, jusqu'à ce qu'il ne reste plus que 111. le dernier chiffre, arrêtez de compter. 🎜🎜Implémentation du code🎜🎜Selon les idées ci-dessus, implémentons le code :🎜// 用位运算实现加法
public static int add(int a, int b) {
int sum = 0;
while (b != 0) {
sum = a ^ b;
b = (a & b) << 1;
a = sum;
}
return sum;
}
// 用位运算实现减法
public static int multi(int a, int b) {
int res = 0;
while (b != 0) {
if ((b & 1) != 0) {
res = add(res, a);
}
a <<= 1;
b >>>= 1;
}
return res;
}Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!