Comment appeler et implémenter la méthode des moindres carrés en Python

La méthode dite des moindres carrés linéaires peut être comprise comme une continuation de la résolution d'équations. La différence est que lorsque la quantité inconnue est bien inférieure au nombre d'équations, un problème insoluble sera obtenu. L'essence de la méthode des moindres carrés est d'attribuer des valeurs aux nombres inconnus tout en garantissant une erreur minimale.

La méthode des moindres carrés est un algorithme très classique, et nous avons été exposés à ce nom au lycée. C'est un algorithme extrêmement couramment utilisé. J'ai déjà écrit sur le principe des moindres carrés linéaires et l'ai implémenté en Python : les moindres carrés et son implémentation Python et comment appeler les moindres carrés non linéaires dans scipy : les moindres carrés non linéaires (contenu supplémentaire à la fin de l'article) ; et Méthode des moindres carrés pour les matrices clairsemées : méthode des moindres carrés des matrices clairsemées.

Ce qui suit décrit la méthode des moindres carrés linéaires implémentée dans numpy et scipy, et compare la vitesse des deux.

Implémentation numpy

La méthode des moindres carrés est implémentée dans numpy, c'est-à-dire que lstsq(a,b) est utilisé pour résoudre x similaire à a@x=b, où a est une matrice de M×N alors lorsque b; Si M lignes de vecteurs sont exactement équivalentes à la résolution d’un système d’équations linéaires. Pour un système d'équations comme Ax=b, si A est une simulation de rang complet, elle peut être exprimée par x=A^&moins;1b, sinon elle peut être exprimée par x=(A^TA) ^&moins;1A^Tb.

Lorsque b est une matrice de M×K, alors pour chaque colonne, un ensemble de x sera calculé.

Il existe 4 valeurs de retour, qui sont le x obtenu par ajustement, l'erreur d'ajustement, le rang de la matrice a et la forme à valeur unique de la matrice a.

import numpy as np
np.random.seed(42)
M = np.random.rand(4,4)
x = np.arange(4)
y = M@x
xhat = np.linalg.lstsq(M,y)
print(xhat[0])
#[0. 1. 2. 3.]

scipy package

scipy.linalg fournit également la fonction des moindres carrés, le nom de la fonction est également lstsq et sa liste de paramètres est

lstsq(a, b, cond=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)

où a, b est Ax=b, les deux fournissent des commutateurs remplaçables, en supposant qu'Etre vrai peut gagner du temps d'exécution. De plus, la fonction prend également en charge la vérification de la finitude, qui est une option proposée par de nombreuses fonctions de linalg. Sa valeur de retour est la même que la fonction des moindres carrés dans numpy.

cond est un paramètre à virgule flottante, indiquant le seuil de valeur singulière lorsque la valeur singulière est inférieure à cond, elle sera ignorée.

lapack_driver est une option de chaîne, indiquant quel moteur d'algorithme dans LAPACK est sélectionné, éventuellement 'gelsd', 'gelsy', 'gelss'.

import scipy.linalg as sl
xhat1 = sl.lstsq(M, y)
print(xhat1[0])
# [0. 1. 2. 3.]

Comparaison de vitesse

Enfin, faites une comparaison de vitesse entre les deux ensembles de fonctions des moindres carrés

from timeit import timeit
N = 100
A = np.random.rand(N,N)
b = np.arange(N)

timeit(lambda:np.linalg.lstsq(A, b), number=10)
# 0.015487500000745058
timeit(lambda:sl.lstsq(A, b), number=10)
# 0.011151800004881807

Cette fois, il n'y a pas un grand écart entre les deux Même si la dimension de la matrice est agrandie à 500, la. deux C'est aussi une demi-douzaine.

N = 500
A = np.random.rand(N,N)
b = np.arange(N)

timeit(lambda:np.linalg.lstsq(A, b), number=10)
0.389679799991427
timeit(lambda:sl.lstsq(A, b), number=10)
0.35642060000100173

Supplément

Python appelle la méthode des moindres carrés non linéaires

Introduction et constructeur

Dans scipy, le but de la méthode des moindres carrés non linéaires est de trouver un ensemble de fonctions qui minimisent la somme des carrés du fonction d'erreur, elle peut être exprimée comme la formule suivante

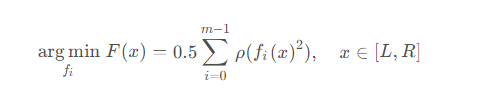
où ρ représente la fonction de perte, qui peut être comprise comme un prétraitement de f_i(x).

scipy.optimize encapsule la fonction des moindres carrés non linéaires least_squares, qui est définie comme

least_squares(fun, x0, jac, bounds, method, ftol, xtol, gtol, x_scale, f_scale, loss, jac_sparsity, max_nfev, verbose, args, kwargs)

Parmi eux, func et x0 sont des paramètres obligatoires, func est la fonction à résoudre et x0 est la valeur initiale de l'entrée de fonction là-bas. est non La valeur par défaut est un paramètre qui doit être saisi.

bound est l'intervalle de solution, la valeur par défaut est (−∞,∞). Lorsque verbose est 1, il y aura une sortie de fin. Lorsque verbose est 2, plus d'informations pendant l'opération seront imprimées. De plus, les paramètres suivants sont utilisés pour contrôler l'erreur, ce qui est relativement simple.

	Valeur par défaut	Remarques
ftol	10-8	Tolérance de fonction
xtol	1 0-8	Tolérance variable indépendante
gtol	10-8	Tolérance de gradient
x_scale	1.0	Échelle caractéristique de la variable
f_scale	1.0	Valeur marginale du résidu

loss为损失函数，就是上面公式中的ρ \rhoρ，默认为linear，可选值包括

迭代策略

上面的公式仅给出了算法的目的，但并未暴露其细节。关于如何找到最小值，则需要确定搜索最小值的方法，method为最小值搜索的方案，共有三种选项，默认为trf

• trf：即Trust Region Reflective，信赖域反射算法

• dogbox：信赖域狗腿算法

• lm：Levenberg-Marquardt算法

这三种方法都是信赖域方法的延申，信赖域的优化思想其实就是从单点的迭代变成了区间的迭代，由于本文的目的是介绍scipy中所封装好的非线性最小二乘函数，故而仅对其原理做简略的介绍。

其中r为置信半径，假设在这个邻域内，目标函数可以近似为线性或二次函数，则可通过二次模型得到区间中的极小值点s_k。然后以这个极小值点为中心，继续优化信赖域所对应的区间。

雅可比矩阵

在了解了信赖域方法之后，就会明白雅可比矩阵在数值求解时的重要作用，而如何计算雅可比矩阵，则是接下来需要考虑的问题。jac参数为计算雅可比矩阵的方法，主要提供了三种方案，分别是基于两点的2-point；基于三点的3-point；以及基于复数步长的cs。一般来说，三点的精度高于两点，但速度也慢一倍。

此外，可以输入自定义函数来计算雅可比矩阵。

测试

最后，测试一下非线性最小二乘法

import numpy as np
from scipy.optimize import least_squares

def test(xs):
    _sum = 0.0
    for i in range(len(xs)):
        _sum = _sum + (1-np.cos((xs[i]*i)/5)*(i+1))
    return _sum

x0 = np.random.rand(5)
ret = least_squares(test, x0)
msg = f"最小值" + ", ".join([f"{x:.4f}" for x in ret.x])
msg += f"\nf(x)={ret.fun[0]:.4f}"
print(msg)
'''
最小值0.9557, 0.5371, 1.5714, 1.6931, 5.2294
f(x)=0.0000
'''

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!