Comment implémenter un algorithme de tri Python de type fusion

Description de l'algorithme

Le premier algorithme de tri avancé de cette section est le tri par fusion. Le mot « fusion » signifie « fusionner ». Comme son nom l'indique, l'algorithme de tri par fusion est un algorithme qui divise d'abord la séquence en sous-séquences, trie les sous-séquences, puis fusionne les sous-séquences ordonnées en une séquence ordonnée complète. Il a en fait adopté l’idée de diviser pour mieux régner.

La complexité temporelle moyenne du tri par fusion est O(nlgn), la complexité temporelle dans le meilleur des cas est O(nlgn) et la complexité temporelle dans le pire des cas est également O(nlgn). Sa complexité spatiale est O(1). De plus, le tri par fusion est un algorithme de tri stable.

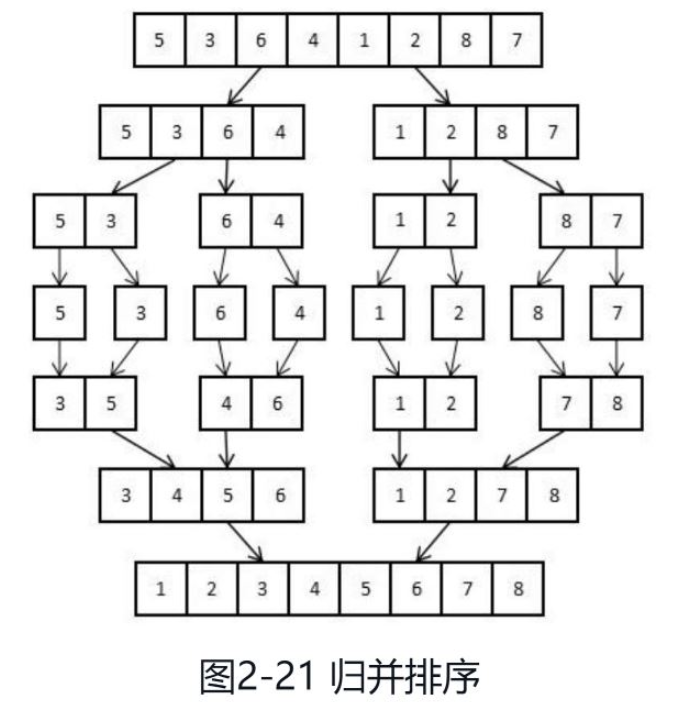
En prenant le tri ascendant comme exemple, le processus de l'algorithme de fusion est illustré à la figure 2-21.

Le tableau d'origine est un tableau non ordonné de 8 nombres. Après une opération, le tableau de 8 nombres est divisé en deux tableaux non ordonnés de 4 nombres. Chaque opération divise le tableau non ordonné en deux jusqu'à ce que tous les plus petits sous-tableaux ne contiennent qu'un seul élément. Lorsqu'il n'y a qu'un seul élément dans le tableau, le tableau doit être ordonné. Ensuite, le programme commence à fusionner tous les deux petits tableaux ordonnés en un grand tableau ordonné. Tout d'abord, fusionnez deux tableaux contenant un nombre dans un tableau contenant deux nombres, puis fusionnez deux tableaux contenant deux nombres dans un tableau contenant quatre nombres, et enfin fusionnez-les dans un tableau contenant huit nombres. Lorsque tous les tableaux ordonnés sont combinés, le tableau ordonné le plus long formé est trié.

Implémentation du code

Fusionner le code de tri :

  #归并排序
nums = [5,3,6,4,1,2,8,7]
def MergeSort(num):
  if(len(num)<=1):　　　　　　　　#递归边界条件
   return num　　　　　　　　　#到达边界时返回当前的子数组
  mid = int(len(num)/2)　　　　　 #求出数组的中位数
  llist,rlist = MergeSort(num[:mid]),MergeSort(num[mid:])#调用函数分别为左右数组排序
  result = []
  i,j = 0,0
  while i < len(llist) and j < len(rlist): #while循环用于合并两个有序数组
   if rlist[j]<llist[i]:
     result.append(rlist[j])
     j += 1
   else:
     result.append(llist[i])
     i += 1
  result += llist[i:]+rlist[j:]　 #把数组未添加的部分加到结果数组末尾
  return result　　　　　　　　　#返回已排序的数组
print(MergeSort(nums))

Exécutez le programme et le résultat de sortie est :

[1,2,3,4,5,6,7,8]

Dans la fonction MergeSort(), la première chose à faire est de juger les conditions aux limites. Lorsqu'un tableau contenant un seul élément est passé en paramètre de fonction, l'élément seul existe dans le tableau, le tableau a donc atteint sa taille minimale. Une fois que vous avez terminé la tâche de décomposition récursive du tableau, ramenez simplement le tableau décomposé au niveau de récursion précédent.

Si la longueur du tableau non trié est toujours supérieure à 1, utilisez la variable mid pour stocker l'indice central du tableau et divisez le tableau non trié en deux sous-tableaux à gauche et à droite. Ensuite, créez deux nouveaux tableaux pour stocker les sous-tableaux gauche et droit triés. L'idée de récursion est utilisée ici. Nous considérons la fonction MergeSort() uniquement comme une fonction qui trie une liste, bien qu'à l'intérieur de la fonction MergeSort(), la fonction elle-même puisse également être appelée pour trier deux sous-tableaux.

Ensuite, utilisez une boucle while pour fusionner les deux tableaux déjà triés. Puisque la taille relative des éléments dans les deux tableaux ne peut pas être déterminée, nous utilisons deux variables, i et j, pour marquer les positions des éléments en attente d'ajout dans le sous-tableau gauche et le sous-tableau droit respectivement. Lorsque la boucle while se termine, il peut rester certains éléments les plus grands à la fin d'un sous-tableau qui n'ont pas été ajoutés à la liste de résultats, donc l'instruction result+=llist[i:]+rlist[j:] vise à empêcher ces éléments d'être manqué. Une fois la fusion du tableau terminée, la fonction génère un tableau ordonné.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!