
En adoptant une stratégie de mise en cache, l'espace peut être converti en temps, améliorant ainsi les performances du système informatique. Le rôle de la mise en cache dans le code est d'optimiser la vitesse d'exécution du code, même si cela augmentera l'empreinte mémoire.
Dans le module functools intégré de Python, la fonction d'ordre supérieur cache() est fournie pour implémenter la mise en cache, qui est utilisée comme décorateur : @cache.
Dans le code source du cache, la description du cache est : Cache simple et illimité Parfois appelé « memoize ». Mise en cache légère et illimitée. Parfois appelé « mémorisation ».
def cache(user_function, /):
'Simple lightweight unbounded cache. Sometimes called "memoize".'
return lru_cache(maxsize=None)(user_function)cache() n'a qu'une seule ligne de code, appelant la fonction lru_cache() et passant un paramètre maxsize=None. lru_cache() est également une fonction du module functools. Vérifiez le code source de lru_cache(). La valeur par défaut de maxsize est 128, ce qui signifie que le maximum de données mises en cache est de 128. Si les données dépassent 128, elles seront supprimées en conséquence. aux données de l’algorithme LRU (Longest Unused). cache() définit maxsize sur None, puis la fonctionnalité LRU est désactivée et le nombre de caches peut augmenter à l'infini, c'est pourquoi on l'appelle "cache illimité".
lru_cache() utilise l'algorithme LRU (Least Récemment Utilisé), qui n'a pas été utilisé depuis longtemps. C'est pourquoi il y a trois lettres lru dans le nom de la fonction. Le mécanisme de l'algorithme le moins utilisé est que, en supposant qu'une donnée n'a pas été consultée au cours de la période récente, la possibilité qu'elle soit consultée dans le futur est également très faible. L'algorithme LRU choisit d'éliminer les données les moins récemment utilisées et de conserver celles qui le sont. sont des données fréquemment utilisées.
cache() est nouveau dans la version Python 3.9, lru_cache() est nouveau dans la version Python 3.2, cache() annule la limite du nombre de caches basée sur lru_cache() , en fait, c'est liés au progrès technologique et à l'amélioration substantielle des performances matérielles, cache() et lru_cache() ne sont que des versions différentes de la même fonction.
lru_cache() est essentiellement un décorateur qui fournit une fonction de cache pour la fonction. Il met en cache le groupe maxsize de paramètres entrants et renvoie directement le résultat précédent la prochaine fois que la fonction est appelée avec. les mêmes paramètres Utilisés pour enregistrer le temps d’appel des fonctions à forte surcharge ou à E/S élevées.
Les scénarios d'application de mise en cache sont très larges, comme la mise en cache de contenu Web statique, qui peut être ajouté directement à la fonction pour que les utilisateurs accèdent aux pages Web statiques. @cache decorator.
Dans certains codes récursifs, le même paramètre est transmis à plusieurs reprises pour exécuter le code de fonction. L'utilisation du cache peut éviter des calculs répétés et réduire la complexité temporelle du code.
Ensuite, j'utiliserai la séquence de Fibonacci comme exemple pour illustrer le rôle de @cache Si vous avez encore un peu de compréhension du contenu précédent, je pense que vous serez éclairé après avoir lu l'exemple.
La suite de Fibonacci fait référence à une suite de nombres : 1, 1, 2, 3, 5, 8, 13, 21, 34,..., à partir du troisième chiffre, chaque chiffre est la somme des deux premiers nombres. La plupart des débutants ont écrit du code pour la séquence de Fibonacci. Son implémentation n'est pas difficile en Python, le code est très concis. Comme suit :
def feibo(n):
# 第0个数和第1个数为1
a, b = 1, 1
for _ in range(n):
# 将b赋值给a,将a+b赋值给b,循环n次
a, b = b, a+b
return aBien sûr, il existe de nombreuses façons d'implémenter le code séquence de Fibonacci (au moins cinq ou six). Afin d'illustrer le scénario d'application de @cache, cet article utilise une méthode d'écriture récursive. Fibonacci Le code de la séquence d'actes. Comme suit :
def feibo_recur(n):
if n < 0:
return "n小于0无意义"
# n为0或1时返回1(前两个数为1)
if n == 0 or n == 1:
return 1
# 根据斐波那契数列的定义,其他情况递归返回前两个数之和
return feibo_recur(n-1) + feibo_recur(n-2)Lorsque le code récursif est exécuté, il récurrera jusqu'à feibo_recur(1) et feibo_recur(0), comme le montre la figure ci-dessous (en prenant le sixième nombre comme exemple ).
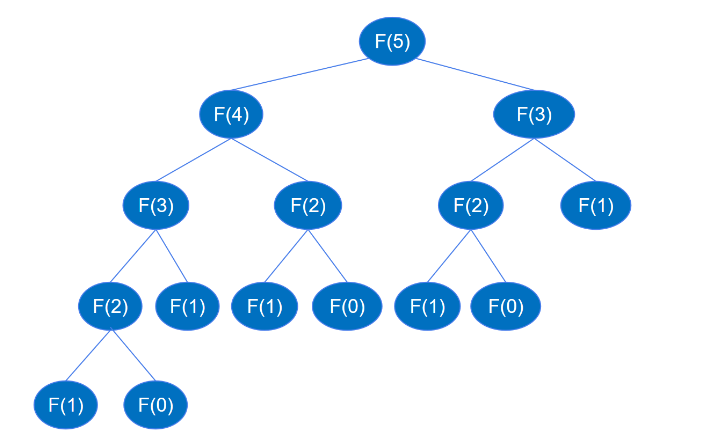
Lorsque vous trouvez F(5), vous devez d'abord trouver F(4) et F(3), et lorsque vous trouvez F(4), vous doit d'abord trouver F( 3) et F(2),... et ainsi de suite, le processus récursif est similaire au processus de parcours en profondeur d'abord d'un arbre binaire. On sait qu'un arbre binaire de hauteur k peut avoir jusqu'à 2k-1 nœuds. D'après le diagramme d'appel récursif ci-dessus, la hauteur de l'arbre binaire est n et les nœuds sont au plus 2n-1. des appels de fonction récursifs est au plus 2n-1 fois, donc la complexité temporelle de la récursivité est O(2^n).
Lorsque la complexité temporelle est O(2^n), le temps d'exécution change de manière très exagérée à mesure que n augmente. Testons-le en pratique.
import time
for i in [10, 20, 30, 40]:
start = time.time()
print(f'第{i}个斐波那契数:', feibo_recur(i))
end = time.time()
print(f'n={i} Cost Time: ', end - start)Sortie :
Comme le montre le temps d'exécution, lorsque n est très petit, la course est très rapide, à mesure que n augmente, le temps d'exécution augmente rapidement Surtout lorsque n. augmente progressivement jusqu'à 30 et 40, la durée de fonctionnement change de manière particulièrement évidente. Afin de voir plus clairement le modèle de changement d’heure, d’autres tests ont été effectués.Le 10ème numéro de Fibonacci : 89
n=10 Coût Temps : 0.0
Le 20ème numéro de Fibonacci : 10946
n=20 Temps de coût : 0.0015988349914550781
Le 30ème numéro de Fibonacci : 1346269
n=30 Temps de coût : 0.17051291465759277# 🎜🎜#40ème Fibonacci numéros : 165580141
n=40 Coût Temps : 20.90010976791382
for i in [41, 42, 43]:
start = time.time()
print(f'第{i}个斐波那契数:', feibo_recur(i))
end = time.time()
print(f'n={i} Cost Time: ', end - start)Le 41ème numéro de Fibonacci : 267914296n=41 Coût Temps : 33.77224683761597
42 Le premier nombre de Fibonacci : 433494437
n=42 Temps de coût : 55.86398696899414
Le 43ème numéro de Fibonacci : 701408733
n=43 Temps de coût : 92.55108690261841# 🎜🎜#
从上面的变化可以看到,时间是指数级增长的(大约按1.65的指数增长),这跟时间复杂度为 O(2^n) 相符。按照这个时间复杂度,假如要计算第50个斐波那契数列,差不多要等一个小时,非常不合理,也说明递归的实现方式运算量过大,存在明显的不足。如何解决这种不足,降低运算量呢?接下来看如何进行优化。
根据前面的分析,递归代码运算量大,是因为递归执行时会不断的计算 feibo_recur(n-1) 和 feibo_recur(n-2),如示例图中,要得到 feibo_recur(5) ,feibo_recur(1) 调用了5次。随着 n 的增大,调用次数呈指数级增长,导致出现大量的重复操作,浪费了许多时间。
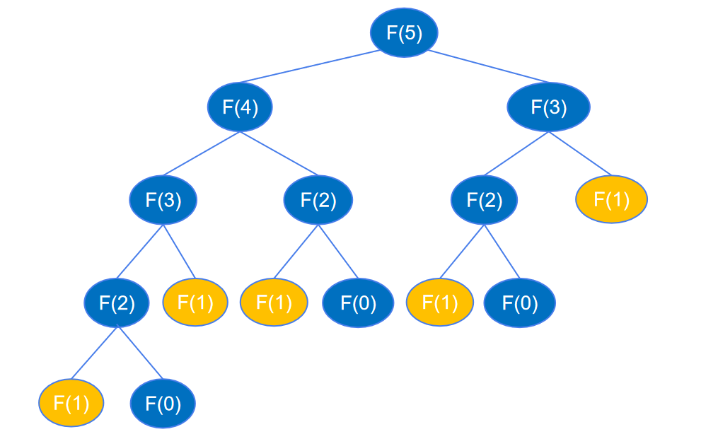
假如有一个地方将每个 n 的执行结果记录下来,当作“备忘录”,下次函数再接收到这个相同的参数时,直接从备忘录中获取结果,而不用去执行递归的过程,就可以避免这些重复调用。在 Python 中,可以创建一个字典或列表来当作“备忘录”使用。
temp = {} # 创建一个空字典,用来记录第i个斐波那契数列的值
def feibo_recur_temp(n):
if n < 0:
return "n小于0无意义"
# n为0或1时返回1(前两个数为1)
if n == 0 or n == 1:
return 1
if n in temp: # 如果temp字典中有n,则直接返回值,不调用递归代码
return temp[n]
else:
# 如果字典中还没有第n个斐波那契数,则递归计算并保存到字典中
temp[n] = feibo_recur_temp(n-1) + feibo_recur_temp(n-2)
return temp[n]上面的代码中,创建了一个空字典用于存放每个 n 的执行结果。每次调用函数,都先查看字典中是否有记录,如果有记录就直接返回,没有记录就递归执行并将结果记录到字典中,再从字典中返回结果。这里的递归其实都只执行了一次计算,并没有真正的递归,如第一次传入 n 等于 5,执行 feibo_recur_temp(5),会递归执行 n 等于 4, 3, 2, 1, 0 的情况,每个 n 计算过一次后 temp 中都有了记录,后面都是直接到 temp 中取数相加。每个 n 都是从temp中取 n-1 和 n-2 的值来相加,执行一次计算,所以时间复杂度是 O(n) 。
下面看一下代码的运行时间。
for i in [10, 20, 30, 40, 41, 42, 43]:
start = time.time()
print(f'第{i}个斐波那契数:', feibo_recur_temp(i))
end = time.time()
print(f'n={i} Cost Time: ', end - start)
print(temp)Output:
第10个斐波那契数: 89
n=10 Cost Time: 0.0
第20个斐波那契数: 10946
n=20 Cost Time: 0.0
第30个斐波那契数: 1346269
n=30 Cost Time: 0.0
第40个斐波那契数: 165580141
n=40 Cost Time: 0.0
第41个斐波那契数: 267914296
n=41 Cost Time: 0.0
第42个斐波那契数: 433494437
n=42 Cost Time: 0.0
第43个斐波那契数: 701408733
n=43 Cost Time: 0.0
{2: 2, 3: 3, 4: 5, 5: 8, 6: 13, 7: 21, 8: 34, 9: 55, 10: 89, 11: 144, 12: 233, 13: 377, 14: 610, 15: 987, 16: 1597, 17: 2584, 18: 4181, 19: 6765, 20: 10946, 21: 17711, 22: 28657, 23: 46368, 24: 75025, 25: 121393, 26: 196418, 27: 317811, 28: 514229, 29: 832040, 30: 1346269, 31: 2178309, 32: 3524578, 33: 5702887, 34: 9227465, 35: 14930352, 36: 24157817, 37: 39088169, 38: 63245986, 39: 102334155, 40: 165580141, 41: 267914296, 42: 433494437, 43: 701408733}
可以观察到,代码的运行时间已经减少到小数点后很多位了(时间过短,只显示了0.0)。然而,temp 字典存储了每个数字的斐波那契数,这需要使用额外的内存空间,以换取更高的时间效率。
上面的代码也可以用列表来当“备忘录”,代码如下。
temp = [1, 1]
def feibo_recur_temp(n):
if n < 0:
return "n小于0无意义"
if n == 0 or n == 1:
return 1
if n < len(temp):
return temp[n]
else:
# 第一次执行时,将结果保存到列表中,后续直接从列表中取
temp.append(feibo_recur_temp(n-1) + feibo_recur_temp(n-2))
return temp[n]现在,已经剖析了递归代码重复执行带来的时间复杂度问题,也给出了优化时间复杂度的方法,让我们将注意力转回到本文介绍的 @cache 装饰器。@cache 装饰器的作用是将函数的执行结果缓存,在下次以相同参数调用函数时直接返回上一次的结果,与上面的优化方式完全一致。
所以,只需要在递归函数上加 @cache 装饰器,递归的重复执行就可以解决,时间复杂度就能从 O(2^n) 降为 O(n) 。代码如下:
from functools import cache
@cache
def feibo_recur(n):
if n < 0:
return "n小于0无意义"
if n == 0 or n == 1:
return 1
return feibo_recur(n-1) + feibo_recur(n-2)使用 @cache 装饰器,可以让代码更简洁优雅,并且让你专注于处理业务逻辑,而不需要自己实现缓存。下面看一下实际的运行时间。
for i in [10, 20, 30, 40, 41, 42, 43]:
start = time.time()
print(f'第{i}个斐波那契数:', feibo_recur(i))
end = time.time()
print(f'n={i} Cost Time: ', end - start)Output:
第10个斐波那契数: 89
n=10 Cost Time: 0.0
第20个斐波那契数: 10946
n=20 Cost Time: 0.0
第30个斐波那契数: 1346269
n=30 Cost Time: 0.0
第40个斐波那契数: 165580141
n=40 Cost Time: 0.0
第41个斐波那契数: 267914296
n=41 Cost Time: 0.0
第42个斐波那契数: 433494437
n=42 Cost Time: 0.0
第43个斐波那契数: 701408733
n=43 Cost Time: 0.0
完美地解决了问题,所有运行时间都被精确到了小数点后数位(即使只显示 0.0),非常巧妙。若今后遇到类似情形,可以直接采用 @cache 实现缓存功能,通过“记忆化”处理。
@cache和@lru_cache(maxsize=None)可以用来寄存函数对已处理参数的结果,以便遇到相同参数可以直接给出答案。前者无限制存储数量,而后者通过设定maxsize限制存储数量的上限。
例:
@lru_cache(maxsize=None) # 等价于@cache
def test(a,b):
print('开始计算a+b的值...')
return a + b可以用来做某些递归、动态规划。比如斐波那契数列的各项值从小到大输出。其实类似用数组保存前项的结果,都需要额外的空间。不过用装饰器可以省略额外空间代码,减少了出错的风险。
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!