Quels sont le cadre de collecte et les algorithmes courants de la structure des données Java ?-javaDidacticiel-php.cn

1 Collection Framework

1.1 Collection Framework Concept

Java Collection FrameworkJava Collection Framework, également connu sous le nom de conteneur, il s'agit d'un ensemble d'interfaces et de ses classes d'implémentation définies dans le package java.util.

Sa principale performance est de placer plusieurs éléments dans une seule unité, qui est utilisée pour stocker, récupérer et gérer rapidement et facilement ces éléments, ce que nous appelons habituellement l'ajout, la suppression et la modification. .

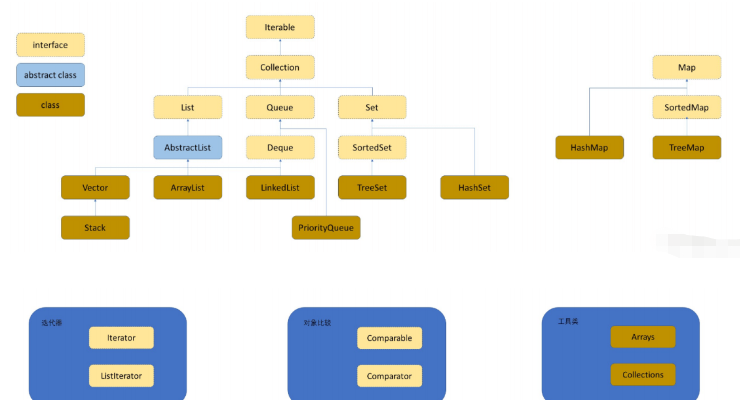
Aperçu des classes et des interfaces :

Quels sont le cadre de collecte et les algorithmes courants de la structure des données Java ?

1.2 Structures de données impliquées dans le conteneur

Collection : Oui Une interface qui contient certaines méthodes couramment utilisées par la plupart des conteneurs

List : C'est une interface qui standardise les méthodes à implémenter dans ArrayList et LinkedList

#🎜 🎜#ArrayList : implémente l'interface List, la couche inférieure est une liste de séquences de type dynamique
LinkedList : implémente l'interface List, la couche inférieure est doublement liée list

Stack : la couche inférieure est une pile et la pile est une table de séquence spéciale

Queue : la couche inférieure est une file d'attente , et la file d'attente est une table de séquence spéciale

#🎜 🎜#Deque : C'est une interface

Set : Set, c'est une interface, et le modèle K est placé à l'intérieur #🎜🎜 #

HashSet : La couche inférieure est le bucket Ha Hi, la complexité temporelle de la requête est O(1)

TreeSet : La couche inférieure est un arbre rouge-noir, la complexité temporelle de la requête est O(), à propos de la clé Séquentielle
Map : cartographie, qui stocke le paires clé-valeur du modèle K-V

HashMap : la couche inférieure est un seau de hachage et la complexité temporelle de la requête est O(1)

TreeMap : La couche inférieure est un arbre rouge-noir et la complexité du temps de requête est O(), à propos de la clé ordonnée
#🎜🎜 #2 Algorithme
2.1 Concept d'algorithme

Algorithme : C'est un calcul bien défini Un processus qui prend une valeur ou un ensemble de valeurs en entrée et produit une valeur ou un ensemble de valeurs en sortie. Un algorithme est une série d’étapes de calcul conçues pour transformer les données d’entrée en résultats de sortie.

2.2 Efficacité des algorithmes

L'analyse de l'efficacité des algorithmes est divisée en deux types : le premier est l'efficacité du temps et le second est l'efficacité de l'espace. L’efficacité temporelle est appelée complexité temporelle, tandis que l’efficacité spatiale est appelée complexité spatiale. La complexité temporelle mesure principalement la vitesse d'exécution d'un algorithme, tandis que la complexité spatiale mesure principalement l'espace supplémentaire requis par un algorithme. Au début du développement informatique, la capacité de stockage des ordinateurs était très faible. Nous nous soucions donc beaucoup de la complexité de l’espace. Avec le développement rapide de l’industrie informatique, la capacité de stockage des ordinateurs a atteint un niveau très élevé. Nous n’avons donc plus besoin de prêter une attention particulière à la complexité spatiale d’un algorithme.

3 Complexité temporelle

3.1 Concept de complexité temporelle

La complexité temporelle est une fonction mathématique en informatique qui représente le temps d'exécution d'un algorithme, qui décrit quantitativement l’efficacité temporelle de l’algorithme. Il est impossible en théorie de calculer le temps d’exécution d’un algorithme. Ce temps ne peut être connu qu’après l’exécution effective du programme sur l’ordinateur. Bien que chaque algorithme puisse être testé sur un ordinateur, cela est très fastidieux, il existe donc un moyen de l'analyser en fonction de la complexité temporelle. La complexité temporelle d'un algorithme est proportionnelle au temps nécessaire pour exécuter les instructions, et la complexité temporelle dépend du nombre d'exécutions des opérations de base de l'algorithme.

3.2 Représentation asymptotique de Big O

// 请计算一下func1基本操作执行了多少次？
void func1(int N){
	int count = 0;
	for (int i = 0; i < N ; i++) {
		for (int j = 0; j < N ; j++) {
			count++;
		}
	}
	for (int k = 0; k < 2 * N ; k++) {
		count++;
	} 
	int M = 10;
	while ((M--) > 0) {
		count++;
	} 
	System.out.println(count);
}

Copier après la connexion

Func1 Le nombre d'opérations de base effectuées : F(N)=N^2+2*N+10

# 🎜 🎜#

N = 10 F(N) = 130

# 🎜 🎜#
N = 1000 F(N) = 1002010
En fait, quand on calcule la complexité temporelle, on n'est pas forcément à calculons le nombre exact d'exécutions, mais seul le nombre approximatif d'exécutions est nécessaire, alors nous utilisons ici la représentation asymptotique du grand O.
Notation Big O : C'est un symbole mathématique utilisé pour décrire le comportement asymptotique d'une fonction
3.3 Dérivation de la méthode du Big O-order

Remplacez toutes les constantes additives du runtime par la constante 1.

Dans la fonction de nombre d'exécutions modifié, seul le terme d'ordre le plus élevé est conservé.

Si le terme d'ordre le plus élevé existe et n'est pas 1, supprimez la constante multipliée par ce terme. Le résultat est l’ordre Big O.
Après avoir utilisé la représentation asymptotique de Big O, la complexité temporelle de Func1 est : O(n^2)
N = 10 F(N) = 100

N = 100 F(N) = 10000

N = 1000 F(N) = 1000000
À travers le contenu ci-dessus, nous pouvons voir que l'exclusion de la notation asymptotique Big O a peu d'impact sur le éléments de résultats, exprimant ainsi de manière concise et claire le nombre d’exécutions. De plus, il existe le meilleur, la moyenne et le pire des cas pour la complexité temporelle de certains algorithmes :
Pire des cas : le nombre maximum d'exécutions (limite supérieure) pour n'importe quelle taille d'entrée
Meilleur cas : le nombre minimum d'exécutions (limite inférieure) pour n'importe quelle taille d'entrée

Meilleur cas : 1 fois trouvé

Pire cas : N fois trouvé

平均情况：N/2次找到

在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)

4 空间复杂度

对于一个算法而言，空间复杂度表示它在执行期间所需的临时存储空间大小。空间复杂度的计算方式并非程序所占用的字节数量，因为这并没有太大的意义；实际上，空间复杂度的计算基于变量的数量。大O渐进表示法通常用来计算空间复杂度，其计算规则类似于实践复杂度的计算规则。

实例1:

// 计算bubbleSort的空间复杂度？
void bubbleSort(int[] array) {
	for (int end = array.length; end > 0; end--) {
		boolean sorted = true;
		for (int i = 1; i < end; i++) {
			if (array[i - 1] > array[i]) {
				Swap(array, i - 1, i);
				sorted = false;
			}
		} 
		if(sorted == true) {
		break;
		}
	}
}

Copier après la connexion

实例2:

// 计算fibonacci的空间复杂度？
int[] fibonacci(int n) {
	long[] fibArray = new long[n + 1];
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n ; i++) {
		fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
	} 
	return fibArray;
}

Copier après la connexion

实例3:

// 计算阶乘递归Factorial的空间复杂度？
long factorial(int N) {
	return N < 2 ? N : factorial(N-1)*N;
}

Copier après la connexion

实例1使用了常数个额外空间，所以空间复杂度为 O(1)
实例2动态开辟了N个空间，空间复杂度为 O(N)
实例3递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!