Comment implémenter un algorithme de classification d'arbre de décision en python

Pré-information

1. Arbre de décision

Phrase réécrite : Dans l'apprentissage supervisé, un algorithme de classification couramment utilisé est l'arbre de décision, qui est basé sur un lot d'échantillons, chaque échantillon contient un ensemble d'attributs et les résultats de classification correspondants. En utilisant ces échantillons à des fins d'apprentissage, l'algorithme peut générer un arbre de décision capable de classer correctement les nouvelles données

2. Exemples de données

Supposons qu'il y ait 14 utilisateurs existants, leurs attributs personnels et leurs données sur l'achat ou non d'un certain produit. Comme suit :

Instable PauvreOui 04>40MoyenInstablePauvreOui05&g t;40FaibleStable pireest 06>40FaibleStableBonneNon0730-40FaibleStable Bienest08MoyenInstableFaibleNonPauvreOui 10>40 ModéréStableFaibleOui11MoyenStableBonOui12 30-40MoyenInstable BonOui1330-40ÉlevéStableFaibleOui14>40Moyen InstableBonNon

Certains algorithmes de classification d'arbres

1. Construire un ensemble de données

Afin de faciliter le traitement, les données de simulation sont converties en données de liste numérique selon les règles suivantes :

Âge :

Revenu : faible est 0 ; moyen est 1 ; élevé est 2

Nature du travail : instable est 0 

Note de crédit ; : Mauvais est 0 ; Bon est 1

#创建数据集
def createdataset():
    dataSet=[[0,2,0,0,'N'],
            [0,2,0,1,'N'],
            [1,2,0,0,'Y'],
            [2,1,0,0,'Y'],
            [2,0,1,0,'Y'],
            [2,0,1,1,'N'],
            [1,0,1,1,'Y'],
            [0,1,0,0,'N'],
            [0,0,1,0,'Y'],
            [2,1,1,0,'Y'],
            [0,1,1,1,'Y'],
            [1,1,0,1,'Y'],
            [1,2,1,0,'Y'],
            [2,1,0,1,'N'],]
    labels=['age','income','job','credit']
    return dataSet,labels

Fonction d'appel, données disponibles :

ds1,lab = createdataset()
print(ds1)
print(lab)

[[0, 2, 0, 0, «N’], [0, 2, 0, 1, «N’ ], [1, 2, 0, 0, «Y’], [2, 1, 0, 0, «Y’], [2, 0, 1, 0, «Y’], [2, 0, 1, 1, «N’], [1, 0, 1, 1, «Y’], [0, 1, 0, 0, «N’], [0, 0, 1, 0 , «Y’], [2, 1, 1, 0, «Y’], [0, 1, 1, 1, «Y’], [1, 1, 0, 1, «Y’ ], [1, 2, 1, 0, « ;Y’], [2, 1, 0, 1, «N’]]
[«âge», «revenu», «emploi», « ;credit’]

2. Entropie des informations sur l'ensemble de données

L'entropie de l'information, également connue sous le nom d'entropie de Shannon, est l'attente d'une variable aléatoire. Mesure le degré d’incertitude de l’information. Plus l’entropie de l’information est grande, plus il est difficile de la comprendre. Le traitement de l'information consiste à clarifier l'information, ce qui est le processus de réduction de l'entropie.

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        
        labelCounts[currentLabel] += 1            
        
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob*log(prob,2)
    
    return shannonEnt

Entropie des informations sur les données d'échantillon :

shan = calcShannonEnt(ds1)
print(shan)

0.9402859586706309

3 Gain d'informations

Gain d'informations : utilisé pour mesurer la contribution de l'attribut A à la réduction de l'entropie de l'ensemble d'échantillons X. Plus le gain d’information est grand, plus il est adapté à la classification de X.

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0])-1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0;bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntroy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prop = len(subDataSet)/float(len(dataSet))
            newEntroy += prop * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntroy
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i    
    return bestFeature

Le code ci-dessus implémente l'algorithme d'apprentissage de l'arbre de décision ID3 basé sur le gain d'entropie de l'information. Son principe logique de base est le suivant : sélectionner tour à tour chaque attribut de l'ensemble d'attributs et diviser l'ensemble d'échantillons en plusieurs sous-ensembles en fonction de la valeur de cet attribut ; calculer l'entropie d'information de ces sous-ensembles et la différence entre celle-ci et l'entropie d'information de l'échantillon est le gain d'entropie d'information de la segmentation par cet attribut ; trouver l'attribut correspondant au gain le plus important parmi tous les gains, qui est l'attribut utilisé pour segmenter l'ensemble d'échantillons.

Calculez le meilleur attribut d'échantillon fractionné de l'échantillon et le résultat est affiché dans la colonne 0, qui est l'attribut d'âge :

col = chooseBestFeatureToSplit(ds1)
col

0

4 Construisez un arbre de décision

def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classList.iteritems(),key=operator.itemgetter(1),reverse=True)#利用operator操作键值排序字典
    return sortedClassCount[0][0]

#创建树的函数    
def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
        
    return myTree

majorityCnt</. La fonction code> est utilisée pour le traitement. La situation suivante : l'arbre de décision idéal final doit atteindre le bas le long de la branche de décision et tous les échantillons doivent avoir le même résultat de classification. Cependant, dans les échantillons réels, il est inévitable que tous les attributs soient cohérents mais que les résultats de classification soient différents. Dans ce cas, <code>majorityCnt ajuste les étiquettes de classification de ces échantillons au résultat de classification comportant le plus d'occurrences. majorityCnt函数用于处理一下情况：最终的理想决策树应该沿着决策分支到达最底端时，所有的样本应该都是相同的分类结果。但是真实样本中难免会出现所有属性一致但分类结果不一样的情况，此时majorityCnt将这类样本的分类标签都调整为出现次数最多的那一个分类结果。

createTree

createTree est la fonction de tâche principale. Il appelle l'algorithme de gain d'entropie des informations ID3 pour tous les attributs en séquence à calculer et à traiter, et génère enfin un arbre de décision.

5. Construire un arbre de décision par instanciation

Construire un arbre de décision à l'aide d'exemples de données :

Tree = createTree(ds1, lab)
print("样本数据决策树：")
print(Tree)

Exemple d'arbre de décision de données :
{‘âge’ : {0 : {‘emploi’ : {0 : ‘ N’, 1 : «Y’}},
1 : «Y’,

2 : {«crédit» : {0 : «Y’, 1 : «N’}}}}

6. Classification de l'échantillon de test

Donnez à un nouvel utilisateur des informations pour déterminer s'il achètera un certain produit :

Numéro	Âge	Fourchette de revenus	Nature de l'emploi	Note de crédit	Décision d'achat
01		Élevé	Instable	Pauvre Non

ÂgeGamme de revenusNature du travailNote de crédit< 30faiblestablebonne<30élevéeinstablebonne

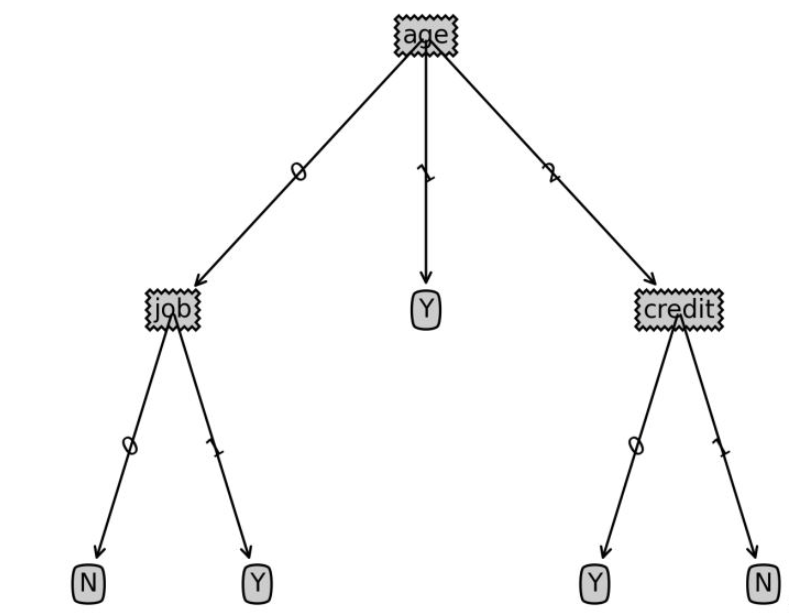
def classify(inputtree,featlabels,testvec):
    firststr = list(inputtree.keys())[0]
    seconddict = inputtree[firststr]
    featindex = featlabels.index(firststr)
    for key in seconddict.keys():
        if testvec[featindex]==key:
            if type(seconddict[key]).__name__=='dict':
                classlabel=classify(seconddict[key],featlabels,testvec)
            else:
                classlabel=seconddict[key]
    return classlabel

labels=['age','income','job','credit']
tsvec=[0,0,1,1]
print('result:',classify(Tree,labels,tsvec))
tsvec1=[0,2,0,1]
print('result1:',classify(Tree,labels,tsvec1))

résultat : N

post-information : tirage des décisions Code d'arbre

Le code suivant est utilisé pour dessiner des graphiques d'arbre de décision, et non l'objectif de l'algorithme d'arbre de décision. Si vous êtes intéressé, vous pouvez vous y référer pour référence

import matplotlib.pyplot as plt

decisionNode = dict(box, fc="0.8")
leafNode = dict(box, fc="0.8")
arrow_args = dict(arrow)

#获取叶节点的数目
def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#测试节点的数据是否为字典，以此判断是否为叶节点
            numLeafs += getNumLeafs(secondDict[key])
        else:   numLeafs +=1
    return numLeafs

#获取树的层数
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#测试节点的数据是否为字典，以此判断是否为叶节点
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:   thisDepth = 1
        if thisDepth > maxDepth: maxDepth = thisDepth
    return maxDepth

#绘制节点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt,  xycoords='axes fraction',
             xytext=centerPt, textcoords='axes fraction',
             va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )

#绘制连接线  
def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)

#绘制树结构  
def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on
    numLeafs = getNumLeafs(myTree)  #this determines the x width of this tree
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]     #the text label for this node should be this
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    plotMidText(cntrPt, parentPt, nodeTxt)
    plotNode(firstStr, cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':#test to see if the nodes are dictonaires, if not they are leaf nodes   
            plotTree(secondDict[key],cntrPt,str(key))        #recursion
        else:   #it's a leaf node print the leaf node
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD

#创建决策树图形    
def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)    #no ticks
    #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0;
    plotTree(inTree, (0.5,1.0), '')
    plt.savefig('决策树.png',dpi=300,bbox_inches='tight')
    plt.show()

.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!