Les opérations sur les nombres sont une exigence très courante dans les bases de données, telles que le calcul de la quantité, du poids, du prix, etc. Afin de répondre à divers besoins, les systèmes de bases de données prennent généralement en charge des types de nombres précis et des types de nombres approximatifs précis. Les types numériques incluent int, décimal, etc. La position du point décimal de ces types est fixée pendant le processus de calcul, et leurs résultats et leur comportement sont relativement prévisibles. Ce problème est particulièrement important lorsqu'il s'agit d'argent, c'est pourquoi certaines bases de données implémentent des types d'argent spécialisés. . Approximation Les types de nombres incluent float, double, etc., et la précision de ces nombres est flottante
L'utilisation du type décimal est similaire dans la plupart des bases de données. Prenons l'exemple du type décimal de MySQL. l'utilisation de base de la décimale. .
Différent du float et du double, le décimal doit spécifier deux nombres décrivant la précision lors de sa création, à savoir la précision et l'échelle. La précision fait référence au nombre total de chiffres dans la décimale entière. y compris les parties entières et décimales, et l'échelle fait référence à Combien de nombres la partie décimale de la décimale contient-elle ? Par exemple : 123,45 est une décimale avec une précision = 5 et une échelle = 2 Nous pouvons définir la décimale que nous voulons de cette manière lors de la construction. la table.
Vous pouvez définir une décimale comme celle-ci lors de la création d'une table :
create table t(d decimal(5, 2));
Vous pouvez y insérer des données légales, par exemple
insert into t values(123.45); insert into t values(123.4);
Si vous exécutez select * from t à ce moment-là, vous obtiendrez
+--------+ | d | +--------+ | 123.45 | | 123.40 | +--------+
Remarquez que 123,4 devient 123,40, c'est la caractéristique du type précis. Chaque ligne de données dans la colonne d nécessite une échelle = 2, c'est-à-dire qu'il y a deux chiffres après. le point décimal
Lors de l'insertion de données qui ne répondent pas aux définitions de précision et d'échelle
insert into t values(1123.45); ERROR 1264 (22003): Out of range value for column 'd' at row 1 insert into t values(123.456); Query OK, 1 row affected, 1 warning show warnings; +-------+------+----------------------------------------+ | Level | Code | Message | +-------+------+----------------------------------------+ | Note | 1265 | Data truncated for column 'd' at row 1 | +-------+------+----------------------------------------+ select * from t; +--------+ | d | +--------+ | 123.46 | +--------+
similaire à 1234,5 (précision=5, échelle=1) Ce nombre semble répondre aux exigences, mais en fait il doit répondre aux exigences de échelle=2, il deviendra donc 1234,50 (précision=6, échelle=2) ce qui ne répond pas aux exigences
Les résultats calculés ne sont pas limités par la définition, mais sont affectés par la. format d'implémentation interne. Pour MySQL, le résultat maximum peut être précision = 81, échelle = 30, mais en raison des problèmes de format de mémoire et d'implémentation de la fonction de calcul de MySQL, cette taille n'est pas Elle peut être obtenue dans toutes les situations, ce qui sera présenté en détail plus tard. En continuant avec l'exemple ci-dessus :
select d + 9999.999 from t; +--------------+ | d + 9999.999 | +--------------+ | 10123.459 | +--------------+
Le résultat dépasse les limites de précision=5, échelle=2. Cela implique le changement d'échelle pendant le fonctionnement. La règle de base est :
Addition/soustraction. /sum : Prendre la plus grande échelle des deux côtés
Multiplication : Additionner les échelles des deux côtés
Division : Échelle du dividende + div_precision_increment (dépend de l'implémentation de la base de données)
Dans cette partie, nous présentons principalement l'implémentation décimale de MySQL. De plus, nous comparerons également ClickHouse pour voir les différences dans la conception et l'implémentation de la décimale dans différents systèmes.
Pour implémenter la décimale, vous devez prendre en compte les problèmes suivants.
Quel degré de précision est pris en charge ? Et l'échelle
Où stocker l'échelle
Pendant une multiplication ou une division continue, l'échelle continue de croître, et la partie entière continue également de s'étendre, et la taille du tampon stocké toujours a une limite supérieure. Comment devrions-nous gérer cela ?
La division peut produire des décimales infinies. Comment déterminer l'échelle du résultat de la division ?
Y a-t-il un conflit entre la plage de représentation des décimales et les performances de calcul ? MySQL
typedef int32 decimal_digit_t;
struct decimal_t {
int intg, frac, len;
bool sign;
decimal_digit_t *buf;
};// 123.45 decimal(5, 2) 整数部分为 3, 小数部分为 2
decimal_t dec_123_45 = {
int intg = 3;
int frac = 2;
int len = 9;
bool sign = false;
decimal_digit_t *buf = {123, 450000000, ...};
};MySQL doit utiliser deux decimal_digit_t (int32) pour stocker 123,45, le premier est 123, combinés. avec intg=3, cela signifie que la partie entière est 123, et le deuxième nombre est 450000000 (un total de 9 nombres), car frac=2, ce qui signifie que la partie décimale est 0,45
Regardons un exemple plus grand :
// decimal(81, 18) 63 个整数数字, 18 个小数数字, 用满整个 buffer
// 123456789012345678901234567890123456789012345678901234567890123.012345678901234567
decimal_t dec_81_digit = {
int intg = 63;
int frac = 18;
int len = 9;
bool sign = false;
buf = {123456789, 12345678, 901234567, 890123456, 789012345, 678901234, 567890123, 12345678, 901234567}
};Cet exemple utilise 81 nombres, mais il existe certains scénarios dans lesquels 81 nombres ne peuvent pas être utilisés. Cela est dû aux entiers et aux décimales. Les parties sont stockées séparément, donc un decimal_digit_t (int32) ne peut stocker qu'un seul chiffre décimal valide, mais le reste de la partie ne peut pas être utilisé pour la partie entière. Par exemple, une décimale a 62 chiffres dans la partie entière et 19 chiffres dans la partie décimale (précision=81, échelle=19), alors la partie décimale doit utiliser 3. decimal_digit_t (int32), et la partie entière a encore 54 chiffres, et 62 chiffres ne peuvent pas être stockés. Dans ce cas, MySQL donnera la priorité à la partie entière. Pour répondre aux besoins, tronquer automatiquement la partie après la virgule et la tourner. en décimal (80, 18)
接下来看看 MySQL 如何在这个数据结构上进行运算. MySQL 通过一系列 decimal_digit_t(int32) 来表示一个较大的 decimal, 其计算也是对这个数组中的各个 decimal_digit_t 分别进行, 如同我们在小学数学计算时是一个数字一个数字地计算, MySQL 会把每个 decimal_digit_t 当作一个数字来进行计算、进位. 由于代码较长, 这里不再对具体的代码进行完整的分析, 仅对代码中核心部分进行分析, 如果感兴趣, 可以直接参考 MySQL 源码 strings/decimal.h 和 strings/decimal.cc 中的 decimal_add, decimal_mul, decimal_div 等代码.
准备步骤
在真正计算前, 还需要做一些准备工作：
MySQL 会将数字的个数 ROUND_UP 到 9 的整数倍, 这样后面就可以按照 decimal_digit_t 为单位来进行计算
此外还要针对参与运算的两个 decimal 的具体情况, 计算结果的 precision 和 scale, 如果发现结果的 precision 超过了支持的上限, 那么会按照 decimal_digit_t 为单位减少小数的数字.
在乘法过程中, 如果发生了 2 中的减少行为, 则需要 TRUNCATE 两个运算数, 避免中间结果超出范围.
加法主要步骤
首先, 因为两个数字的 precision 和 scale 可能不相同, 需要做一些准备工作, 将小数点对齐, 然后开始计算, 从最末尾小数开始向高位加, 分为三个步骤：
将小数较多的 decimal 多出的小数数字复制到结果中
将两个 decimal 公共的部分相加
将整数较多的 decimal 多出的整数数字与进位相加到结果中
代码中使用了 stop, stop2 来标记小数点对齐后, 长度不同的数字出现差异的位置.
/* part 1 - max(frac) ... min (frac) */
while (buf1 > stop) *--buf0 = *--buf1;
/* part 2 - min(frac) ... min(intg) */
carry = 0;
while (buf1 > stop2) {
ADD(*--buf0, *--buf1, *--buf2, carry);
}
/* part 3 - min(intg) ... max(intg) */
buf1 = intg1 > intg2 ? ((stop3 = from1->buf) + intg1 - intg2)
: ((stop3 = from2->buf) + intg2 - intg1);
while (buf1 > stop3) {
ADD(*--buf0, *--buf1, 0, carry);
}
乘法主要步骤
乘法引入了一个新的 dec2, 表示一个 64 bit 的数字, 这是因为两个 decimal_digit_t(int32) 相乘后得到的可能会是一个 64 bit 的数字. 在计算时一定要先把类型转换到 dec2(int64), 再计算, 否则会得到溢出后的错误结果. 乘法与加法不同, 乘法不需要对齐, 例如计算 11.11 5.0, 那么只要计算 111150=55550, 再移动小数点位置就能得到正确结果 55.550
MySQL 实现了一个双重循环将 decimal1 的 每一个 decimal_digit_t 与 decimal2 的每一个 decimal_digit_t 相乘, 得到一个 64 位的 dec2, 其低 32 位是当前的结果, 其高 32 位是进位.
typedef decimal_digit_t dec1; typedef longlong dec2;
for (buf1 += frac1 - 1; buf1 >= stop1; buf1--, start0--) {
carry = 0;
for (buf0 = start0, buf2 = start2; buf2 >= stop2; buf2--, buf0--) {
dec1 hi, lo;
dec2 p = ((dec2)*buf1) * ((dec2)*buf2);
hi = (dec1)(p / DIG_BASE);
lo = (dec1)(p - ((dec2)hi) * DIG_BASE);
ADD2(*buf0, *buf0, lo, carry);
carry += hi;
}
if (carry) {
if (buf0 < to->buf) return E_DEC_OVERFLOW;
ADD2(*buf0, *buf0, 0, carry);
}
for (buf0--; carry; buf0--) {
if (buf0 < to->buf) return E_DEC_OVERFLOW;
ADD(*buf0, *buf0, 0, carry);
}
}除法主要步骤
除法使用的是 Knuth's Algorithm D, 其基本思路和手动除法也比较类似.
首先使用除数的前两个 decimal_digit_t 组成一个试商因数, 这里使用了一个 norm_factor 来保证数字在不溢出的情况下尽可能扩大, 这是因为 decimal 为了保证精度必须使用整形来进行计算, 数字越大, 得到的结果就越准确. D3: 猜商, 就是用被除数的前两个 decimal_digit_t 除以试商因数 这里如果不乘 norm_factor, 则 start1[1] 和 start2[1] 都不会体现在结果之中.
D4: 将 guess 与除数相乘, 再从被除数中剪掉结果 然后做一些修正, 移动向下一个 decimal_digit_t, 重复这个过程.
想更详细地了解这个算法可以参考 https://skanthak.homepage.t-online.de/division.html
norm2 = (dec1)(norm_factor * start2[0]); if (likely(len2 > 0)) norm2 += (dec1)(norm_factor * start2[1] / DIG_BASE)；
x = start1[0] + ((dec2)dcarry) * DIG_BASE; y = start1[1]; guess = (norm_factor * x + norm_factor * y / DIG_BASE) / norm2;
for (carry = 0; buf2 > start2; buf1--) {
dec1 hi, lo;
x = guess * (*--buf2);
hi = (dec1)(x / DIG_BASE);
lo = (dec1)(x - ((dec2)hi) * DIG_BASE);
SUB2(*buf1, *buf1, lo, carry);
carry += hi;
}
carry = dcarry < carry;ClickHouse 是列存, 相同列的数据会放在一起, 因此计算时通常也将一列的数据合成 batch 一起计算.
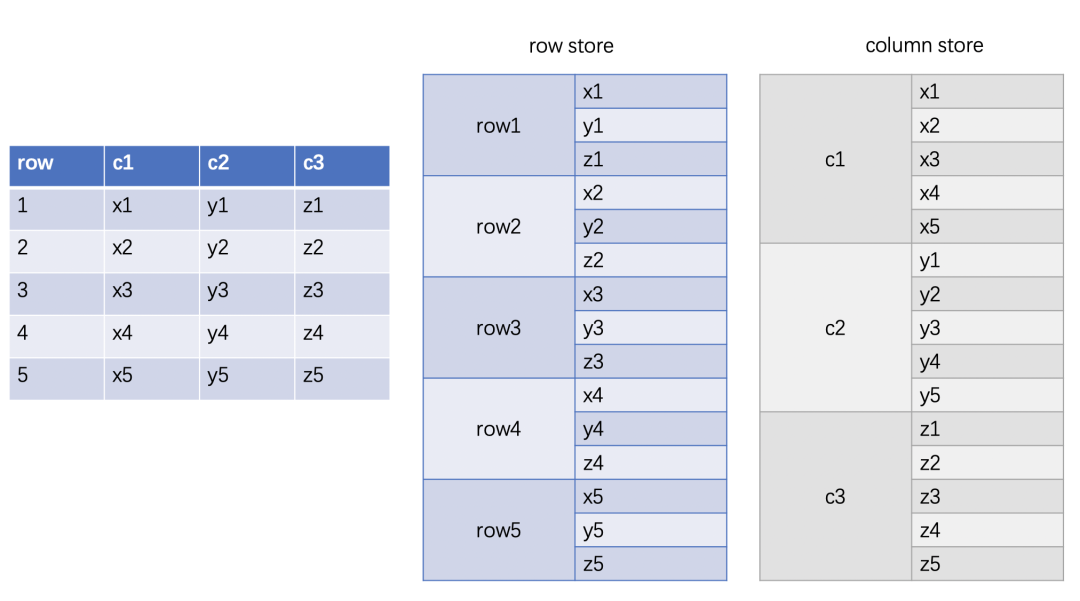
一列的 batch 在 ClickHouse 中使用 PODArray, 例如上图中的 c1 在计算时就会有一个 PODArray, 进行简化后大致可以表示如下:
class PODArray {
char * c_start = null;
char * c_end = null;
char * c_end_of_storage = null;
}在计算时会讲 c_start 指向的数组转换成实际的类型, 对于 decimal, ClickHouse 使用足够大的 int 来表示, 根据 decimal 的 precision 选择 int32, int64 或者 int128. 例如一个 decimal(10, 2), 123.45, 使用这样方式可以表示为一个 int32_t, 其内容为 12345, decimal(10, 3) 的 123.450 表示为 123450. ClickHouse 用来表示每个 decimal 的结构如下, 实际上就是足够大的 int：
template <typename T>
struct Decimal
{
using NativeType = T;
// ...
T value;
};
using Int32 = int32_t;
using Int64 = int64_t;
using Int128 = __int128;
using Decimal32 = Decimal<Int32>;
using Decimal64 = Decimal<Int64>;
using Decimal128 = Decimal<Int128>;显而易见, 这样的表示方法相较于 MySQL 的方法更轻量, 但是范围更小, 同时也带来了一个问题是没有小数点的位置, 在进行加减法、大小比较等需要小数点对齐的场景下, ClickHouse 会在运算实际发生的时候将 scale 以参数的形式传入, 此时配合上面的数字就可以正确地还原出真实的 decimal 值了.
ResultDataType type = decimalResultType(left, right, is_multiply, is_division);
int scale_a = type.scaleFactorFor(left, is_multiply);
int scale_b = type.scaleFactorFor(right, is_multiply || is_division);
OpImpl::vector_vector(col_left->getData(), col_right->getData(), vec_res,
scale_a, scale_b, check_decimal_overflow);例如两个 decimal: a = 123.45000(p=8, s=5), b = 123.4(p=4, s=1), 那么计算时传入的参数就是 col_left->getData() = 123.45000 10 ^ 5 = 12345000, scale_a = 1, col_right->getData() = 123.4 10 ^ 1 = 1234, scale_b = 10000, 12345000 1 和 1234 10000 的小数点位置是对齐的, 可以直接计算.
加法主要步骤
ClickHouse 实现加法同样要先对齐, 对齐的方法是将 scale 较小的数字乘上一个系数, 使两边的 scale 相等. 然后直接做加法即可. ClickHouse 在计算中也根据 decimal 的 precision 进行了细分, 对于长度没那么长的 decimal, 直接用 int32, int64 等原生类型计算就可以了, 这样大大提升了速度.
bool overflow = false;
if constexpr (scale_left)
overflow |= common::mulOverflow(a, scale, a);
else
overflow |= common::mulOverflow(b, scale, b);
overflow |= Op::template apply<NativeResultType>(a, b, res);template <typename T>
inline bool addOverflow(T x, T y, T & res)
{
return __builtin_add_overflow(x, y, &res);
}
template <>
inline bool addOverflow(__int128 x, __int128 y, __int128 & res)
{
static constexpr __int128 min_int128 = __int128(0x8000000000000000ll) << 64;
static constexpr __int128 max_int128 = (__int128(0x7fffffffffffffffll) << 64) + 0xffffffffffffffffll;
res = x + y;
return (y > 0 && x > max_int128 - y) || (y < 0 && x < min_int128 - y);
}乘法主要步骤
同 MySQL, 乘法不需要对齐, 直接按整数相乘就可以了, 比较短的 decimal 同样可以使用 int32, int64 原生类型. int128 在溢出检测时被转换成 unsigned int128 避免溢出时的未定义行为.
template <typename T>
inline bool mulOverflow(T x, T y, T & res)
{
return __builtin_mul_overflow(x, y, &res);
}
template <>
inline bool mulOverflow(__int128 x, __int128 y, __int128 & res)
{
res = static_cast<unsigned __int128>(x) * static_cast<unsigned __int128>(y); /// Avoid signed integer overflow.
if (!x || !y)
return false;
unsigned __int128 a = (x > 0) ? x : -x;
unsigned __int128 b = (y > 0) ? y : -y;
return (a * b) / b != a;
}除法主要步骤
先转换 scale 再直接做整数除法. 本身来讲除法和乘法一样是不需要对齐小数点的, 但是除法不一样的地方在于可能会产生无限小数, 所以一般数据库都会给结果一个固定的小数位数, ClickHouse 选择的小数位数是和被除数一样, 因此需要将 a 乘上 scale, 然后在除法运算的过程中, 这个 scale 被自然减去, 得到结果的小数位数就可以保持和被除数一样.
bool overflow = false;
if constexpr (!IsDecimalNumber<A>)
overflow |= common::mulOverflow(scale, scale, scale);
overflow |= common::mulOverflow(a, scale, a);
if (overflow)
throw Exception("Decimal math overflow", ErrorCodes::DECIMAL_OVERFLOW);
return Op::template apply<NativeResultType>(a, b);MySQL 通过一个 int32 的数组来表示一个大数, ClickHouse 则是尽可能使用原生类型, GCC 和 Clang 都支持 int128 扩展, 这使得 ClickHouse 的这种做法可以比较方便地实现.
MySQL 与 ClickHouse 的实现差别还是比较大的, 针对我们开始提到的问题, 分别来看看他们的解答.
precision 和 scale 范围, MySQL 最高可定义 precision=65, scale=30, 中间结果最多包含 81 个数字, ClickHouse 最高可定义 precision=38, scale=37, 中间结果最大为 int128 的最大值 -2^127 ~ 2^127-1.
在哪里存储 scale, MySQL 是行式存储, 使用火山模型逐行迭代, 计算也是按行进行, 每个 decimal 都有自己的 scale；ClickHouse 是列式存储, 计算按列批量进行, 每行按照相同的 scale 处理能提升性能, 因此 scale 来自表达式解析过程中推导出来的类型.
scale 增长, scale 增长超过极限时, MySQL 会通过动态挤占小数空间, truncate 运算数, 尽可能保证计算完成, ClickHouse 会直接报溢出错.
除法 scale, MySQL 通过 div_prec_increment 来控制除法结果的 scale, ClickHouse 固定使用被除数的 scale.
性能, MySQL 使用了更宽的 decimal 表示, 同时要进行 ROUND_UP, 小数挤占, TRUNCATE 等动作, 性能较差, ClickHouse 使用原生的数据类型和计算最大限度地提升了性能.
在这一部分中, 我们将讲述一些 MySQL 实现造成的违反直觉的地方. 这些行为通常发生在运算结果接近 81 digit 时, 因此如果可以保证运算结果的范围较小也可以忽略这些问题.
乘法的 scale 会截断到 31, 且该截断是通过截断运算数字的方式来实现的, 例如: select 10000000000000000000000000000000.100000000 10000000000000000000000000000000 = 10000000000000000000000000000000.100000000000000000000000000000 10000000000000000000000000000000.555555555555555555555555555555 返回 1, 第二个运算数中的 .555555555555555555555555555555 全部被截断
MySQL 使用的 buffer 包含了 81 个 digit 的容量, 但是由于小数部分必须和整数部分分开, 因此很多时候无法用满 81 个 digit, 例如: select 99999999999999999999999999999999999999999999999999999999999999999999999999.999999 = 99999999999999999999999999999999999999999999999999999999999999999999999999.9 返回 1
计算过程中如果发现整数部分太大会动态地挤占小数部分, 例如: select 999999999999999999999999999999999999999999999999999999999999999999999999.999999999 + 999999999999999999999999999999999999999999999999999999999999999999999999.999999999 = 999999999999999999999999999999999999999999999999999999999999999999999999 + 999999999999999999999999999999999999999999999999999999999999999999999999 返回 1
除法计算中间结果不受 scale = 31 的限制, 除法中间结果的 scale 一定是 9 的整数倍, 不能按照最终结果来推测除法作为中间结果的精度, 例如 select 2.0000 / 3 3 返回 2.00000000, 而 select 2.00000 / 3 3 返回 1.999999998, 可见前者除法的中间结果其实保留了更多的精度.
除法, avg 计算最终结果的小数部分如果正好是 9 的倍数, 则不会四舍五入, 例如: select 2.00000 / 3 返回 0.666666666, select 2.0000 / 3 返回 0.66666667
除法, avg 计算时, 运算数字的小数部分如果不是 9 的倍数, 那么会实际上存储 9 的倍数个小数数字, 因此会出现以下差异：
create table t1 (a decimal(20, 2), b decimal(20, 2), c integer); insert into t1 values (100000.20, 1000000.10, 5); insert into t1 values (200000.20, 2000000.10, 2); insert into t1 values (300000.20, 3000000.10, 4); insert into t1 values (400000.20, 4000000.10, 6); insert into t1 values (500000.20, 5000000.10, 8); insert into t1 values (600000.20, 6000000.10, 9); insert into t1 values (700000.20, 7000000.10, 8); insert into t1 values (800000.20, 8000000.10, 7); insert into t1 values (900000.20, 9000000.10, 7); insert into t1 values (1000000.20, 10000000.10, 2); insert into t1 values (2000000.20, 20000000.10, 5); insert into t1 values (3000000.20, 30000000.10, 2); select sum(a+b), avg(c), sum(a+b) / avg(c) from t1; +--------------+--------+-------------------+ | sum(a+b) | avg(c) | sum(a+b) / avg(c) | +--------------+--------+-------------------+ | 115500003.60 | 5.4167 | 21323077.590317 | +--------------+--------+-------------------+ 1 row in set (0.01 sec) select 115500003.60 / 5.4167; +-----------------------+ | 115500003.60 / 5.4167 | +-----------------------+ | 21322946.369561 | +-----------------------+ 1 row in set (0.00 sec)
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
mysql modifier le nom de la table de données
MySQL crée une procédure stockée
La différence entre MongoDB et MySQL
Comment vérifier si le mot de passe MySQL est oublié
mysql créer une base de données
niveau d'isolement des transactions par défaut de MySQL
La différence entre sqlserver et mysql
mysqlmot de passe oublié
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
