Quelle est la différence entre l'index B-tree et l'index B+-tree dans MySQL ?

Si vous utilisez un arbre comme structure de données d'index, chaque fois que vous recherchez des données, un nœud de l'arborescence sera lu à partir du disque, qui est une page. Cependant, chaque nœud de l'arbre binaire ne stocke qu'une seule donnée. , qui ne peut pas remplir une page d’espace de stockage, l’espace de stockage supplémentaire ne serait-il pas gaspillé ? Afin de résoudre cette lacune de l'arbre de recherche binaire équilibré, nous devrions rechercher une structure de données capable de stocker plus de données dans un seul nœud, c'est-à-dire un arbre de recherche multidirectionnel.

1. Arbre de recherche multidirectionnel

1. Hauteur complète de l'arbre binaire : O(log2N), où 2 est le logarithme, le nombre de nœuds à chaque niveau de l'arbre ; .Arbre de recherche M-way complet La hauteur : O(logmN), où M est le logarithme, le nombre de nœuds dans chaque couche de l'arbre ; O(log2N)，其中2为对数，树每层的节点数；

2、完全M路搜索树的高度：O(logmN)，其中M为对数，树每层的节点数；

M路搜索树适用于存储数据量过大无法一次性加载到内存的场景。通过增加每层节点的个数和在每个节点存放更多的数据来在一层中存放更多的数据，从而降低树的高度，在数据查找时减少磁盘访问次数。

因此，如果每个节点包含的关键字数量和每层的节点数量增加，则树的高度将减少。尽管每个节点的数据确定会更加耗时，但B树的关注点在于解决磁盘性能瓶颈，因此单个节点搜索数据的成本可以被忽略。

2. B树-多路平衡搜索树

B树是一种M路搜索树，B树主要用于解决M路搜索树的不平衡导致树的高度变高，跟二叉树退化为链表导致性能问题一样。B树通过对每层的节点进行控制、调整，如节点分离，节点合并，一层满时向上分裂父节点来增加新的层等操作来来保证该M路搜索树的平衡。

在B树中，每个节点都是一个磁盘块（页），而阶数或者说路数M则规定了节点中最多的子节点数量。每个非叶子节点存放了关键字和指向儿子树的指针，具体数量为：M阶的B树，每个非叶子节点存放了M-1个关键字和M个指向子树的指针。如图为5阶B树结构的示意图：

3. B树索引

首先创建一张user表：

create table user(
	id int,
	name varchar,
	primary key(id)
) ROW_FORMAT=COMPACT;

假如我们使用B树对表中的用户记录建立索引：

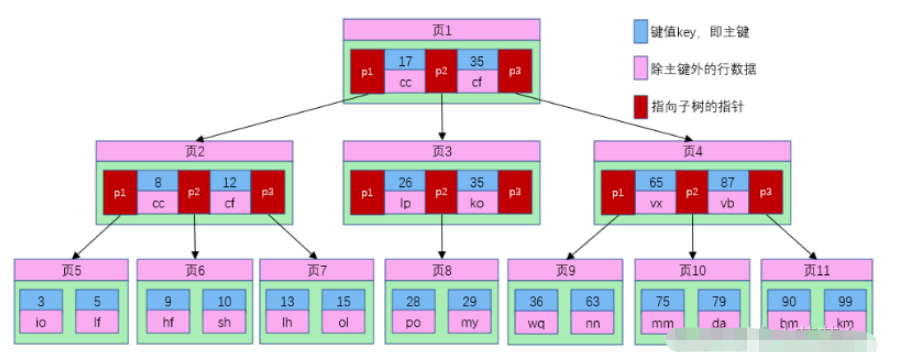
B树的每个节点占用一个磁盘块，磁盘块也就是页，从上图可以看出，B树相对于平衡二叉树，每个节点存储了更多的主键key和数据data，并且每个节点拥有了更多的子节点，子节点的个数一般称为阶，上述图中的B树为3阶B树，高度也会降低。假如我们要查找id=28的用户信息，那么查找流程如下：

1、根据根节点找到页1，读入内存。【磁盘I/O操作第1次】

2、比较键值28在区间（17,35），找到页1的指针p2；

3、根据p2指针找到页3，读入内存。【磁盘I/O操作第2次】

4、比较键值28在区间（26,35），找到页3的指针p2。

5、根据p2指针找到页8，读入内存。【磁盘I/O操作第3次】

6、在页8中的键值列表中找到键值28，键值对应的用户信息为(28,po)；

B-Tree相对于AVLTree

L'arbre de recherche M-way convient aux scénarios ; où la quantité de données stockées est trop importante pour être chargée dans la mémoire en une seule fois. Stockez plus de données dans une couche en augmentant le nombre de nœuds par couche et en stockant plus de données dans chaque nœud, réduisant ainsi la hauteur de l'arborescence et le nombre d'accès au disque lors de la recherche de données.

Donc, si le nombre de mots-clés que contient chaque nœud et le nombre de nœuds par niveau augmentent, la hauteur de l'arbre diminuera. Bien que la détermination des données de chaque nœud prenne plus de temps, l'objectif de B-tree est de résoudre le goulot d'étranglement des performances du disque, de sorte que le coût de la recherche de données sur un seul nœud peut être ignoré.

2. B-Tree - Arbre de recherche équilibré multidirectionnel

B-tree est un arbre de recherche M-way est principalement utilisé pour résoudre le déséquilibre de l'arbre de recherche M-way, qui provoque la hauteur de l'arbre. l'arbre devient plus haut et provoque la dégénérescence de l'arbre binaire en une liste chaînée. Les problèmes de performances sont les mêmes. Le B-tree assure l'équilibre de l'arbre de recherche M-way en contrôlant et en ajustant les nœuds de chaque couche, tels que la séparation des nœuds, la fusion des nœuds, la division des nœuds parents vers le haut lorsqu'une couche est pleine pour ajouter de nouvelles couches, et d'autres opérations.

Dans le B-tree, chaque nœud est un bloc de disque (page), et l'ordre ou le numéro de chemin M spécifie le nombre maximum de nœuds enfants dans le nœud. Chaque nœud non-feuille stocke des mots-clés et des pointeurs vers des sous-arbres. Le numéro spécifique est : arbre B d'ordre M, chaque nœud non-feuille stocke des mots-clés M-1 et des pointeurs M vers des sous-arbres. L'image montre un diagramme schématique de la structure de l'arbre B à 5 ordres :

3. Index B-tree

Créez d'abord une table utilisateur :

rrreeeSi nous utilisons B-tree pour indexer les enregistrements utilisateur dans le tableau :

Chaque nœud du B-tree occupe un bloc de disque, et le bloc de disque est également une page. Comme le montre la figure ci-dessus, comparé à l'arbre binaire équilibré, chaque nœud du L'arbre B stocke plus de clés primaires et de données, et chaque nœud a plus de nœuds enfants, le nombre de nœuds enfants est généralement appelé l'ordre. L'arbre B dans la figure ci-dessus est un arbre B à 3 niveaux et la hauteur. sera également réduite. Si nous voulons trouver les informations utilisateur de id=28, alors le processus de recherche est le suivant :

1 Trouvez la page 1 en fonction du nœud racine et lisez-la dans la mémoire. [Opération d'E/S disque 1ère fois] 🎜🎜2. Comparez la valeur de clé 28 dans l'intervalle (17,35), recherchez le pointeur p2 de la page 1 🎜🎜3. dans la mémoire. [Opération d'E/S disque 2ème fois] 🎜🎜4. Comparez la valeur clé 28 dans l'intervalle (26,35) et trouvez le pointeur p2 de la page 3. 🎜🎜5. Trouvez la page 8 selon le pointeur p2 et lisez-la dans la mémoire. [Opération d'E/S disque 3ème fois] 🎜🎜6. Recherchez la valeur de clé 28 dans la liste des valeurs de clé à la page 8. Les informations utilisateur correspondant à la valeur de clé sont (28,po) ; Par rapport à AVLTree, le nombre de nœuds est réduit, de sorte que les données sont extraites de la mémoire à chaque fois que les E/S du disque sont utilisées, améliorant ainsi l'efficacité des requêtes. 🎜🎜4. B+Tree Index🎜🎜B+Tree est une optimisation basée sur B-Tree, ce qui le rend plus adapté à la mise en œuvre de structures d'index de stockage externes : 🎜🎜1. nœuds Identique au nombre de mots-clés ; 🎜🎜2. Ajoutez un pointeur de lien vers tous les nœuds feuilles ; 🎜🎜3. Tous les mots-clés apparaissent dans les nœuds feuilles, et les mots-clés dans la liste chaînée sont dans l'ordre ; Non Le nœud feuille est équivalent à l'index du nœud feuille, et le nœud feuille est équivalent à la couche de données qui stocke les données (mot-clé) 🎜🎜Le moteur de stockage InnoDB utilise B+Tree pour implémenter sa structure d'index ; 🎜🎜Dans le diagramme de structure B-tree, on peut voir que chaque nœud contient également des valeurs de données en plus de la valeur clé des données. L'espace de stockage de chaque page est limité. Si les données sont volumineuses, le nombre de clés pouvant être stockées dans chaque nœud (c'est-à-dire une page) sera très faible. Lorsque la quantité de données stockées est importante, cela entraînera également. à B- La profondeur de l'arborescence est plus grande, ce qui augmente le nombre d'E/S disque pendant la requête, affectant ainsi l'efficacité de la requête. Dans B+Tree, tous les nœuds d'enregistrement de données sont stockés sur les nœuds feuilles dans la même couche par ordre de valeur clé. Seules les informations sur les valeurs clés sont stockées sur les nœuds non feuilles. Cela peut augmenter considérablement le nombre de valeurs clés stockées dans chacun. node. , réduisez la hauteur de B+Tree. 🎜🎜🎜B+Tree présente plusieurs différences par rapport à B-Tree : 🎜🎜🎜1. Les nœuds non-feuilles stockent uniquement les informations sur les valeurs clés et les pointeurs vers les numéros de page des nœuds enfants. 🎜🎜2. Il existe un lien entre toutes les chaînes de nœuds-feuilles. pointeur ; 🎜🎜3. Les enregistrements de données sont stockés dans les nœuds feuilles ;

D'après la figure ci-dessus, jetons un coup d'œil à la différence entre l'arbre B+ et l'arbre B :

(2) Dans l'arbre B+, les nœuds non-feuilles ne stockent que les valeurs clés, tandis que les nœuds de l'arbre B stockent les deux. valeurs clés et données du magasin.

La taille de la page est fixe et la taille de page par défaut dans InnoDB est de 16 Ko. Si les données ne sont pas stockées, davantage de valeurs clés seront stockées, l'ordre de l'arborescence correspondante sera plus grand et l'arborescence sera plus courte et plus grosse. En conséquence, le nombre de fois d'E/S disque dont nous avons besoin pour rechercher des données. sera à nouveau réduite. L’efficacité des requêtes de données sera également plus rapide.

De plus, si un nœud de notre arbre B+ peut stocker 1 000 valeurs clés, alors l'arbre B+ à 3 couches peut stocker 1 000×1000×1000=1 milliard de données. Généralement, le nœud racine réside en mémoire (il n'est pas nécessaire de lire le disque lors de la première récupération du nœud racine), donc généralement nous n'avons besoin que de 2 E/S disque pour rechercher 1 milliard de données.

(2) Toutes les données de l'index de l'arbre B+ sont stockées dans des nœuds feuilles et les données sont organisées dans l'ordre.

B+ Les pages de l'arborescence sont connectées via une liste chaînée bidirectionnelle, et les données dans les nœuds feuilles sont connectées via une liste chaînée unidirectionnelle De cette façon, toutes les données du tableau peuvent être trouvées. Les arbres B+ rendent les requêtes par plage, les requêtes de tri, les requêtes de groupe et les requêtes de déduplication extrêmement simples. Dans B-tree, les données étant dispersées dans différents nœuds, il n’est pas facile d’y parvenir.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!