
a. C'est un arbre binaire (chaque nœud a au plus deux nœuds enfants)
b Pour la valeur du nœud dans cet arbre
Toutes les valeurs de nœud dans le sous-arbre de gauche
Les valeurs égales ne sont généralement pas prises en compte dans les arbres de recherche binaires (les éléments ne sont pas répétés dans JDK n'a pas la même valeur (TreeMap-key)).
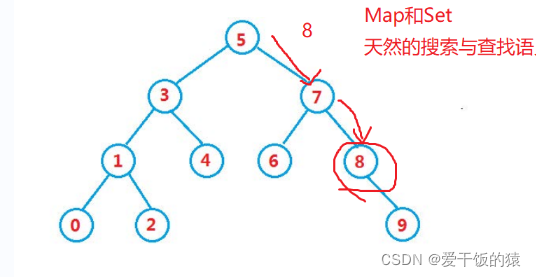
La plus grande fonctionnalité : aussi Comment déterminer s'il s'agit d'un arbre de recherche
Effectuez un parcours dans l'ordre de l'arbre, et vous pouvez obtenir un ensemble ascendant 0 1 2 3 4 5 6 7 8 9
Le complexité temporelle de la recherche binaire sur un intervalle ordonné ? logn Continuer à définir /2/2 / 2 ==1 jusqu'à ce que logN
logN =》associer à "tree"
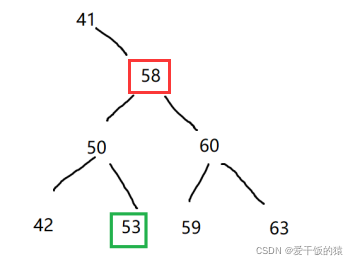
Lorsque 58 est supprimé. , ni le sous-arbre gauche ni le sous-arbre droit de ce nœud n'est vide
Suppression Hibbard 1962
Supprimer un nœud dans le BST qui a à la fois des sous-arbres gauche et droit
Trouver le nœud prédécesseur ou successeur du nœud actuel avec 58 comme racine comme le nouveau nœud après suppression
Prédécesseur : Dans le BST avec 58 comme racine Le dernier nœud inférieur à 58->53
Successeur : Le premier nœud supérieur à 58 dans le BST enraciné à 58->59
Quand nous utilisons le nœud successeur, connectez d'abord removeMin(root.right), même avec root.left
TreeNode successor = findMin(root.right); successor.right = removeMin(root.right); successor.left = root.left;
import java.util.NoSuchElementException;
/**
* 基于整型的
* 普通的二分搜索树
*/
public class BST {
private class TreeNode{
private int val;
private TreeNode left;
private TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
private int size;
private TreeNode root;
/**
* 向以root为根的BST中插入一个新的结点val
* @param val
*/
public void add(int val){
root = add(root,val);
}
private TreeNode add(TreeNode root, int val) {
if(root == null){
//创建一个新节点
TreeNode newNode = new TreeNode(val);
size++;
return newNode;
}
//左子树插入
if(val < root.val){
root.left = add(root.left,val);
}
//右子树插入
if(val > root.val){
root.right = add(root.right,val);
}
return root;
}
/**
* 判断当前以root为根的BST中是否包含了val
* @param val
* @return
*/
public boolean contains(int val){
return contains(root,val);
}
private boolean contains(TreeNode root, int val) {
if(root == null){
return false;
}
if(val == root.val){
//找到了
return true;
}else if(val < root.val){
//递归左子树查找
return contains(root.left,val);
}else{
//递归右子树查找
return contains(root.right,val);
}
}
/**
* 找到最小值
* @return
*/
public int findMin(){
//判空
if(root == null){
//抛出一个空指针异常
throw new NoSuchElementException("root is empty! cannot find min");
}
TreeNode minNode = findMin(root);
return minNode.val;
}
private TreeNode findMin(TreeNode root) {
//当此节点左子树为空,说明此节点是最小值
if(root.left == null){
return root;
}
//递归访问左子树
return findMin(root.left);
}
/**
* 找到最大值
* @return
*/
public int findMax(){
//判空
if(root == null){
throw new NoSuchElementException("root is empty! cannot find max");
}
TreeNode maxNode = findMax(root);
return maxNode.val;
}
private TreeNode findMax(TreeNode root) {
//当此节点右子树为空,说明此节点是最大值
if(root.right == null){
return root;
}
//递归访问右子树
return findMax(root.right);
}
/**
* 在当前BST中删除最小值节点,返回删除的最小值
* @return
*/
public int removeMin(){
int min =findMin();
root = removeMin(root);
return min;
}
private TreeNode removeMin(TreeNode root) {
if(root.left == null){
TreeNode right = root.right;
//找到最小值,删除节点
root = root.left = null;
size--;
return right;
}
root.left = removeMin(root.left);
return root;
}
/**
* 在当前BST中删除最大值节点,返回删除的最大值
* @return
*/
public int removeMax(){
int max = findMax();
root = removeMax(root);
return max;
}
//在当前以root为根的BST中删除最小值所在的节点,返回删除后的树根
private TreeNode removeMax(TreeNode root) {
if(root.right == null){
TreeNode right = root.right;
//找到最大值,删除节点
root = root.right = null;
size--;
return right;
}
root.right = findMax(root.right);
return root;
}
/**
* 在当前以root为根节点的BST中删除值为val的节点
* 返回删除后的新的根节点
* @return
*/
public void removeValue(int value){
root = removeValue(root,value);
}
private TreeNode removeValue(TreeNode root, int value) {
if(root == null){
throw new NoSuchElementException("root is empty! cannot find remove");
}else if(value < root.val){
root.left = removeValue(root.left,value);
return root;
}else if(value > root.val){
root.right = removeValue(root.right,value);
return root;
}else {
//此时value == root.value
if(root.left == null){
//删除最小数
TreeNode right = root.right;
root = root.right = null;
size--;
return right;
}
if(root.right == null){
//删除最大数
TreeNode left = root.left;
root = root.left =null;
size--;
return left;
}
//找到当前该删除节点的前驱或者后继节点作为删除后的新节点
//当我们使用后继节点时,先连removeMin(root.right),在连root.left
TreeNode successor = findMin(root.right);
successor.right = removeMin(root.right);
successor.left = root.left;
return successor;
}
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
generateBSTString(root,0,sb);
return sb.toString();
}
//直观打印,可以看到树的深度
private void generateBSTString(TreeNode root, int height, StringBuilder sb) {
if(root == null){
sb.append(generateHeightString(height)).append("NULL\n");
return;
}
sb.append(generateHeightString(height)).append(root.val).append("\n");
generateBSTString(root.left,height+1,sb);
generateBSTString(root.right,height+1,sb);
}
private String generateHeightString(int height) {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < height; i++) {
sb.append("--");
}
return sb.toString();
}
}Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!