Bien que les modèles de langage à grande échelle aient montré des performances supérieures dans diverses tâches de traitement du langage naturel, les questions arithmétiques restent une grande difficulté, même le GPT-4 le plus puissant est actuellement difficile à gérer.
Récemment, des chercheurs de l'Université nationale de Singapour ont proposé un modèle dédié à l'arithmétique, Goat. Après avoir été affiné sur la base du modèle LLaMA, il a atteint des capacités arithmétiques nettement meilleures que GPT-4.
Lien papier : https://arxiv.org/pdf/2305.14201.pdf
En affinant l'ensemble de données arithmétiques synthétiques, Goat fonctionne bien sur la sous-couche arithmétique BIG-bench sk Atteignant des performances de pointe,
Goat peut atteindre une précision presque parfaite dans les opérations d'addition et de soustraction de grands nombres uniquement grâce à un réglage fin supervisé, surpassant tous les modèles de langage pré-entraînés précédents, tels que Bloom, OPT, et GPT-NeoX, etc. Parmi eux, la précision obtenue par Goat-7B avec zéro échantillon dépasse même le PaLM-540 après un apprentissage en quelques étapes. Les chercheurs attribuent les excellentes performances de Goat à la technologie cohérente de segmentation des mots de LLaMA pour les nombres.
Pour résoudre des tâches plus difficiles telles que la multiplication et la division de grands nombres, les chercheurs ont également proposé une méthode pour classer les tâches en fonction de la capacité d'apprentissage de l'arithmétique, puis utiliser les principes arithmétiques de base pour classer les tâches non apprenables telles que. la multiplication et la division à plusieurs chiffres sont décomposées en une série de tâches apprenables.
Après une vérification expérimentale complète, les étapes de décomposition proposées dans l'article peuvent améliorer efficacement les performances arithmétiques.
Et Goat-7 B peut être entraîné efficacement à l'aide de LoRA sur un GPU VRAM de 24 Go. D'autres chercheurs peuvent répéter l'expérience très facilement. Le modèle, l'ensemble de données et le script Python pour générer l'ensemble de données seront bientôt open source. "Modèle de langage qui peut compter" atteint des performances de pointe sur plusieurs benchmarks.
Les résultats de recherches précédentes montrent que la tokenisation est importante pour la capacité arithmétique de LLM, mais les techniques de tokenisation couramment utilisées ne peuvent pas bien représenter les nombres. Par exemple, les nombres comportant trop de chiffres peuvent être segmentés.
LLaMA choisit de diviser les nombres en plusieurs jetons pour garantir la cohérence de la représentation numérique. Les chercheurs pensent que l'extraordinaire capacité arithmétique démontrée dans les résultats expérimentaux est principalement due à la segmentation cohérente des nombres de LLaMA.
Lors des expériences, d'autres modèles de langage affinés, tels que Bloom, OPT, GPT-NeoX et Pythia, n'ont pas pu égaler les capacités arithmétiques de LLaMA.
Apprentissage des tâches arithmétiques
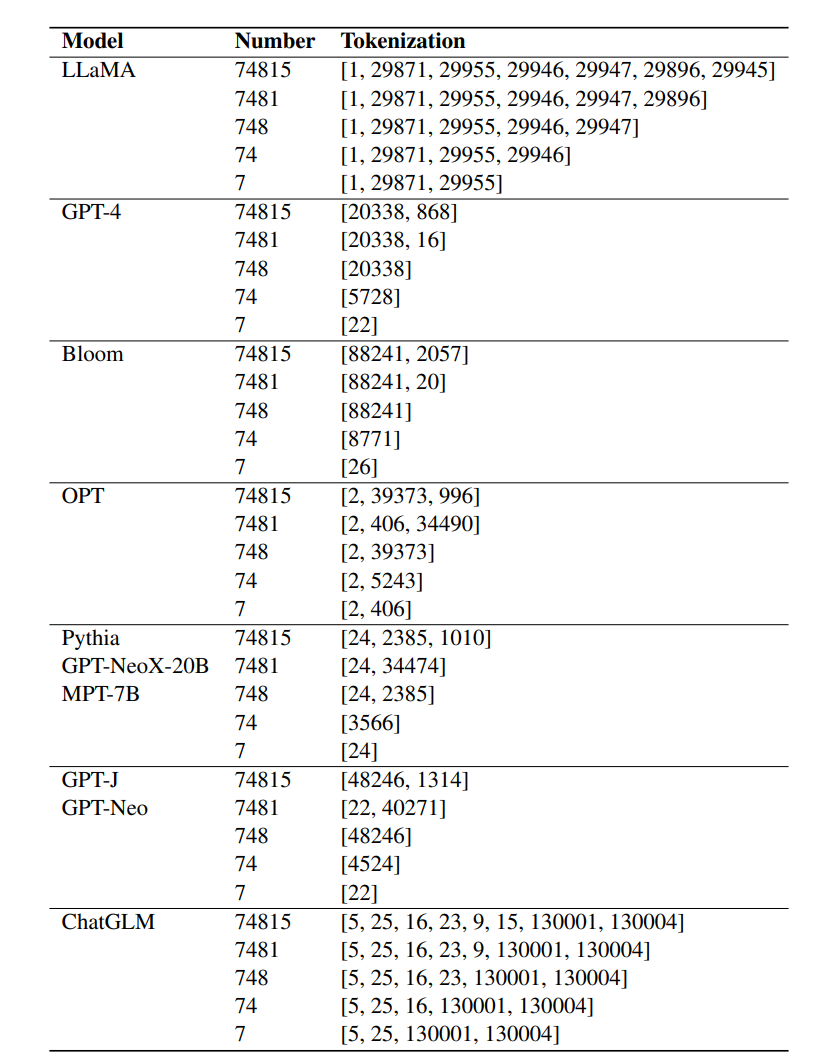
C'est-à-dire que des problèmes composés non apprenables peuvent être appris en utilisant une supervision intermédiaire ou une chaîne d'étapes (CoT).
Sur la base de cette analyse, les chercheurs ont d'abord classé expérimentalement les tâches apprenables et non apprenables.
Dans le contexte du calcul arithmétique, les tâches apprenables font généralement référence aux tâches pour lesquelles un modèle peut être entraîné avec succès pour générer directement des réponses, atteignant ainsi une précision suffisamment élevée dans un nombre prédéfini d'époques d'entraînement. Les tâches impossibles à apprendre sont celles pour lesquelles un modèle a du mal à apprendre correctement et à générer des réponses directes même après une formation approfondie. Bien que les raisons exactes des changements dans la capacité d'apprentissage des tâches ne soient pas entièrement comprises, on peut émettre l'hypothèse que cela est lié à la complexité du modèle sous-jacent et à la taille de la mémoire de travail requise pour accomplir la tâche.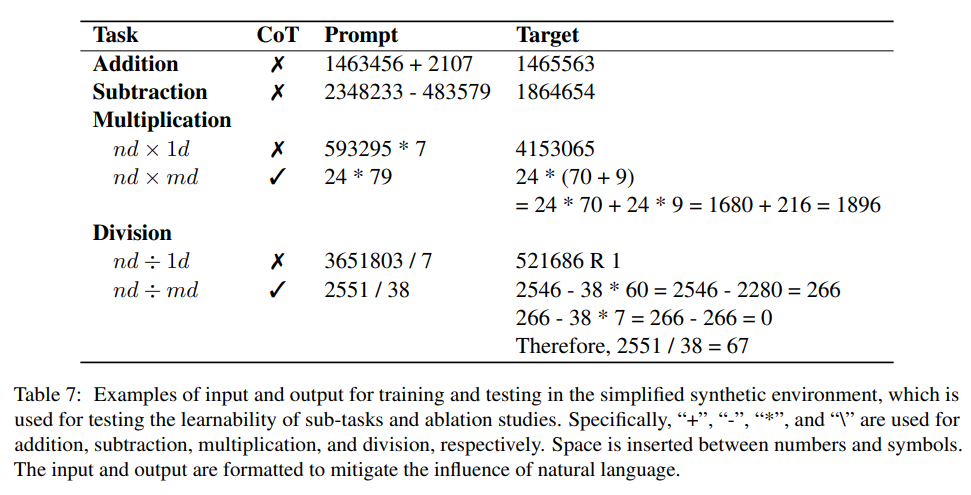 
Les chercheurs ont examiné expérimentalement la capacité d'apprentissage de ces tâches en affinant le modèle spécifiquement pour chaque tâche dans un environnement synthétique simplifié.
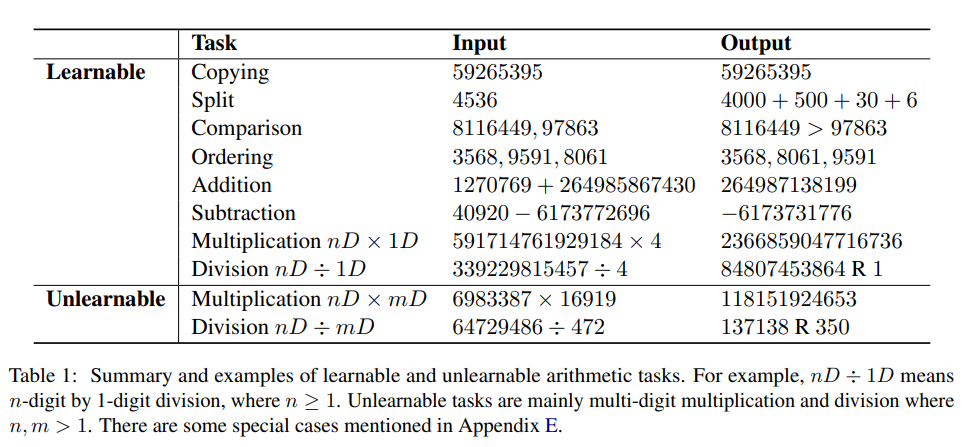
Tâches apprenables et non apprenables
Les résultats de la classification des tâches sont également les mêmes que la perception humaine. Avec de la pratique, les humains peuvent calculer la somme de deux grands nombres dans leur esprit. . Pour la soustraction, vous pouvez écrire la réponse numérique finale directement de gauche (chiffre le plus significatif) vers la droite (chiffre le moins significatif) sans faire de calculs manuels.
Mais le calcul mental pour résoudre la multiplication et la division de grands nombres est une tâche difficile.
On peut également observer que les résultats de classification des tâches ci-dessus sont également cohérents avec les performances de GPT-4, en particulier GPT-4 est efficace pour générer des réponses directes pour l'addition et la soustraction de grands nombres, lorsqu'il s'agit de multi- tâches de multiplication et de division de chiffres, la précision diminuera considérablement.
L'incapacité d'un modèle puissant comme GPT-4 à résoudre directement des tâches non apprenables peut également indiquer qu'il est extrêmement difficile de générer des réponses directes à ces tâches, même après une formation approfondie.
Il convient de noter que les tâches qui peuvent être apprises pour LLaMA ne le sont pas nécessairement pour d'autres LLM.
De plus, toutes les tâches classées comme non-apprenables ne sont pas totalement impossibles à apprendre pour le modèle.
Par exemple, multiplier des nombres à deux chiffres par des nombres à deux chiffres est considéré comme une tâche non apprenable, mais si l'ensemble d'entraînement contient toutes les données d'énumération de multiplication à 2 chiffres possibles, le modèle peut toujours apprendre en surajustant l'ensemble d'entraînement. . Générez directement des réponses.
Cependant, l'ensemble du processus nécessite près de 10 époques pour atteindre une précision d'environ 90 %.
En insérant le CoT proposé dans l'article avant la réponse finale, le modèle peut atteindre une assez bonne précision dans la multiplication à deux chiffres après 1 époque d'entraînement, ce qui est également cohérent avec les conclusions de recherches précédentes, c'est-à-dire le milieu Le la présence d’un encadrement facilite le processus d’apprentissage.
Addition et Soustraction
Ces deux opérations arithmétiques peuvent être apprises, et grâce à un réglage fin supervisé seul, le modèle a démontré une capacité extraordinaire à générer avec précision des réponses numériques directes.
Bien que le modèle n'ait été entraîné que sur un sous-ensemble très limité de données d'addition, le modèle capture avec succès les opérations arithmétiques, comme le montre le fait que le modèle a atteint une précision presque parfaite sur un ensemble de test invisible. Le mode de base sans en utilisant CoT
Multiplication
Les chercheurs ont vérifié expérimentalement que la multiplication à n chiffres par multiplication à 1 chiffre peut être apprise, alors que la multiplication à plusieurs chiffres ne peut pas être apprise.
Pour surmonter ce problème, les chercheurs ont choisi d'affiner le LLM pour générer CoT avant de générer la réponse, en décomposant la multiplication à plusieurs chiffres en 5 sous-tâches apprenables :
1. Extraction, Extraire des expressions arithmétiques du langage naturel. instructions
2. Divisez, divisez la plus petite des deux en valeurs de position
.3. Expansion, basée sur l'expansion distributive et la sommation
4 Produit, calculez chaque produit en même temps
5 En ajoutant terme par terme, en ajoutant le précédent Ajoutez deux termes, copiez les termes restants, et obtenez la somme finale
Chacune de ces tâches est apprenable.
Division
De même, on peut observer expérimentalement que la division de nombres à n chiffres par un nombre à 1 chiffre peut être apprise, tandis que la division à plusieurs chiffres ne peut pas être apprise.
Les chercheurs ont conçu une nouvelle invite de chaîne de réflexion en utilisant l'équation de récursion de division lente améliorée.
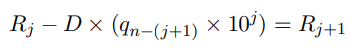
L'idée principale est de soustraire les multiples du diviseur du dividende jusqu'à ce que le reste soit inférieur au diviseur.
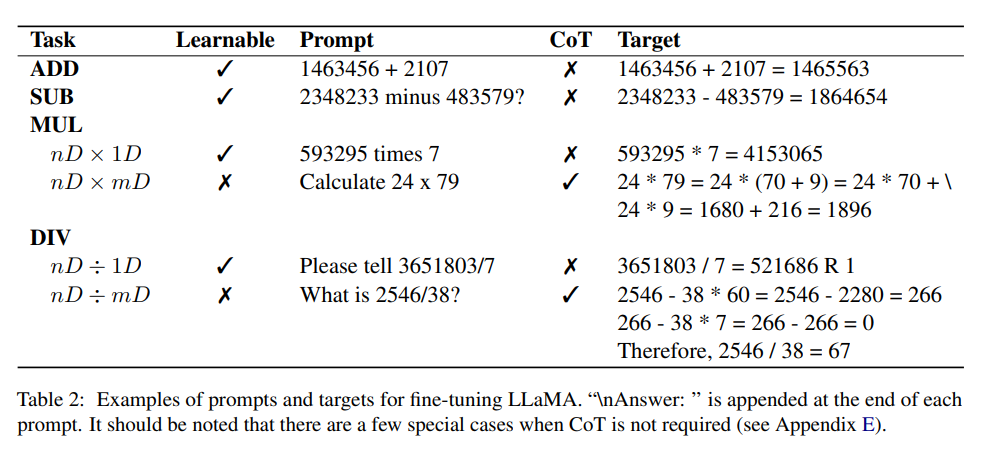
Ensemble de données
L'expérience conçue dans l'article est l'addition et la soustraction de deux entiers positifs. Chaque entier positif contient jusqu'à 16 chiffres, et le résultat de l'opération de soustraction peut être. un nombre négatif.
Afin de limiter la longueur maximale de la séquence générée, le résultat de la multiplication est un entier positif à moins de 12 chiffres ; dans la division de deux entiers positifs, le dividende est inférieur à 12 chiffres et le quotient est inférieur à 6 chiffres.
Les chercheurs ont utilisé un script Python pour synthétiser un ensemble de données et ont généré environ 1 million de paires de questions et réponses. Les réponses contiennent le CoT proposé et la sortie numérique finale. Tous les nombres sont générés de manière aléatoire, ce qui garantit la probabilité de répétition. Le nombre d’instances est très faible, mais de petits nombres peuvent être échantillonnés plusieurs fois.
Réglage fin
Pour permettre au modèle de résoudre des problèmes arithmétiques basés sur des instructions et de faciliter la réponse aux questions en langage naturel, les chercheurs ont utilisé ChatGPT pour générer des centaines de modèles d'instructions.
Pendant le processus de réglage des instructions, un modèle est sélectionné au hasard pour chaque entrée arithmétique de l'ensemble d'entraînement et affiné LLaMA-7B, similaire à la méthode utilisée dans Alpaca.
Goat-7B peut être affiné à l'aide de LoRA sur un GPU VRAM de 24 Go, ce qui ne prend qu'environ 1,5 heure pour compléter 100 000 échantillons sur un GPU A100 et atteindre une précision presque parfaite.
Il semble injuste de comparer les performances de Goat et de GPT-4 en termes de grand nombre de multiplications et de divisions, car GPT-4 génère des réponses directement, tandis que Goat s'appuie sur une chaîne de pensée conçue, donc dans GPT-4 Lors de l'évaluation, "Résolvez-le étape par étape" a également été ajouté à la fin de chaque invite
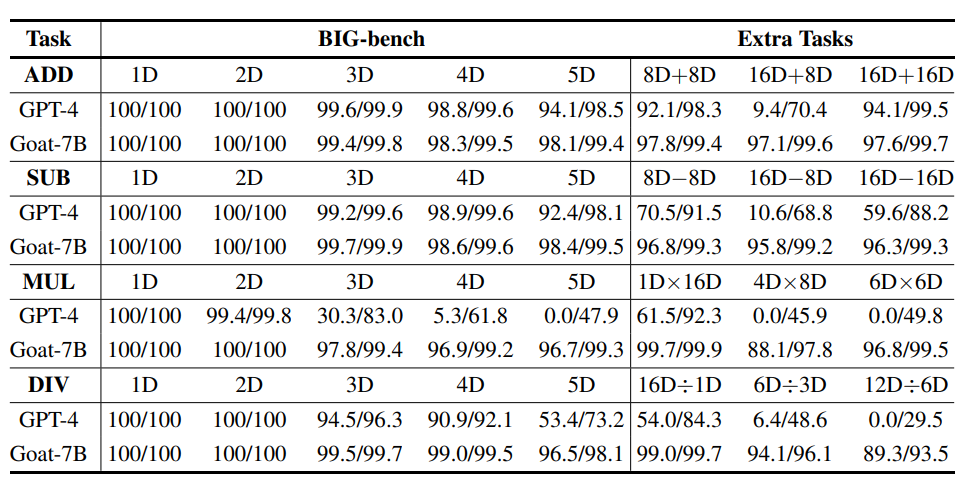
Cependant, on peut observer que bien que GPT-4 dans certains cas, les étapes intermédiaires Les multiplications et divisions longues sont fausses, mais la réponse finale est toujours correcte, ce qui signifie que GPT-4 n'utilise pas la supervision intermédiaire de la chaîne de réflexion pour améliorer le résultat final.
Les 3 erreurs courantes suivantes ont finalement été identifiées à partir de la solution de GPT-4 :
1 Alignement des nombres correspondants
.2. Nombres répétés
3. Le résultat intermédiaire de la multiplication de n chiffres par 1 chiffre est faux
Les résultats expérimentaux montrent que GPT-4 fonctionne bien sur le 8D+8D et le 16D+. Tâches 16D Les performances sont plutôt bonnes, mais les résultats de calcul sont erronés sur la plupart des tâches 16D+8D, même si intuitivement, 16D+8D devrait être relativement plus facile que 16D+16D.
Bien que la cause exacte de ce problème soit inconnue, un facteur possible pourrait être le processus de segmentation des chiffres incohérent de GPT-4, rendant difficile l'alignement entre les deux chiffres.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Comment masquer l'adresse IP sur TikTok
Comment résoudre le problème que cette copie de Windows n'est pas authentique
Comment redémarrer régulièrement
Introduction à l'utilisation de Rowid dans Oracle
Comment résoudre le problème selon lequel le raccourci IE ne peut pas être supprimé
utilisation des instructions mul
Comment ouvrir des fichiers torrent
Comment écrire du code de zone de texte HTML
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
