 Périphériques technologiques
Périphériques technologiques
 IA
IA
 « Mettre » un grand modèle de 33 milliards de paramètres dans un seul GPU grand public, accélérant 15 % sans sacrifier les performances
« Mettre » un grand modèle de 33 milliards de paramètres dans un seul GPU grand public, accélérant 15 % sans sacrifier les performances
« Mettre » un grand modèle de 33 milliards de paramètres dans un seul GPU grand public, accélérant 15 % sans sacrifier les performances
Les performances des grands modèles de langage (LLM) pré-entraînés sur des tâches spécifiques continuent de s'améliorer. Par la suite, si les instructions rapides sont appropriées, elles peuvent être mieux généralisées à davantage de tâches. De nombreuses personnes attribuent ce phénomène à l'augmentation du nombre de tâches. En ce qui concerne la formation des données et des paramètres, les tendances récentes montrent que les chercheurs se concentrent davantage sur des modèles plus petits, mais ces modèles sont formés sur plus de données et sont donc plus faciles à utiliser lors de l'inférence.
Par exemple, LLaMA avec une taille de paramètre de 7B a été formé sur des jetons 1T Bien que les performances moyennes soient légèrement inférieures à GPT-3, la taille du paramètre est de 1/25 de cette dernière. De plus, la technologie de compression actuelle peut compresser davantage ces modèles, réduisant ainsi considérablement les besoins en mémoire tout en maintenant les performances. Grâce à de telles améliorations, des modèles performants peuvent être déployés sur les appareils des utilisateurs finaux tels que les ordinateurs portables.
Cependant, cela se heurte à un autre défi, celui de savoir comment compresser ces modèles dans une taille suffisamment petite pour s'adapter à ces appareils, tout en tenant compte de la qualité de génération. La recherche montre que même si les modèles compressés génèrent des réponses avec une précision acceptable, les techniques de quantification 3 à 4 bits existantes dégradent toujours la précision. Étant donné que la génération LLM est effectuée de manière séquentielle et repose sur des jetons générés précédemment, de petites erreurs relatives s'accumulent et conduisent à une grave corruption de sortie. Pour garantir une qualité fiable, il est essentiel de concevoir des méthodes de quantification à faible largeur de bits qui ne dégradent pas les performances de prédiction par rapport aux modèles 16 bits.
Cependant, la quantification de chaque paramètre sur 3-4 bits entraîne souvent des pertes de précision modérées, voire élevées, en particulier pour les modèles plus petits dans la plage de paramètres 1-10B qui sont idéaux pour le déploiement en périphérie.
Afin de résoudre le problème de précision, des chercheurs de l'Université de Washington, de l'ETH Zurich et d'autres institutions ont proposé un nouveau format de compression et une technologie de quantification SpQR (Sparse-Quantized Representation, représentation clairsemée-quantifiée), qui a été mis en œuvre pour le pour la première fois, LLM fournit une compression quasiment sans perte à toutes les échelles du modèle tout en atteignant des niveaux de compression similaires à ceux des méthodes précédentes.
SpQR fonctionne en identifiant et en isolant les poids anormaux qui provoquent des erreurs de quantification particulièrement importantes, en les stockant avec une plus grande précision tout en compressant tous les autres poids à 3-4 bits, dans LLaMA. Une perte de précision relative de moins de 1 % de perplexité a été obtenue dans et les LLM Falcon. Cela permet d'exécuter un LLM de paramètre 33B sur un seul GPU grand public de 24 Go sans aucune dégradation des performances tout en étant 15 % plus rapide.
L'algorithme SpQR est efficace et peut à la fois encoder les poids dans d'autres formats et les décoder efficacement au moment de l'exécution. Plus précisément, cette recherche fournit à SpQR un algorithme d'inférence GPU efficace qui permet une inférence plus rapide que les modèles de base 16 bits tout en atteignant des gains de compression de mémoire plus de 4 fois.

- Adresse papier : https://arxiv.org/pdf/2306.03078.pdf
- Adresse du projet : https://github.com/Vahe1994/SpQR
Méthode
Cette étude propose un nouveau format pour la quantification clairsemée hybride - Sparse Quantization Representation (SpQR), qui peut compresser avec précision le LLM pré-entraîné à 3-4 bits par paramètre tout en restant presque sans perte.
Plus précisément, l'étude a divisé l'ensemble du processus en deux étapes. La première étape est la détection des valeurs aberrantes : l'étude isole d'abord les poids aberrants et démontre que leur quantification entraîne des erreurs élevées : les poids aberrants sont conservés avec une haute précision, tandis que les autres poids sont stockés avec une faible précision (par exemple dans un format 3 bits). L'étude met ensuite en œuvre une variante de quantification groupée avec des groupes de très petite taille et montre que l'échelle de quantification elle-même peut être quantifiée dans une représentation à 3 bits.
SpQR réduit considérablement l'empreinte mémoire du LLM sans compromettre la précision, tout en produisant un LLM 20 à 30 % plus rapide que l'inférence 16 bits.
De plus, l'étude a révélé que les positions des poids sensibles dans la matrice de poids ne sont pas aléatoires mais ont une structure spécifique. Pour mettre en évidence sa structure lors de la quantification, l'étude a calculé la sensibilité de chaque poids et visualisé ces sensibilités au poids pour le modèle LLaMA-65B. La figure 2 ci-dessous représente la projection de sortie de la dernière couche d'auto-attention de LLaMA-65B. L'étude a apporté deux modifications au processus de quantification : l'une pour capturer les petits groupes de poids sensibles et l'autre pour capturer les valeurs aberrantes individuelles. La figure 3 ci-dessous montre la structure globale de SpQR : la quantification de l'algorithme SpQR, le fragment de code à gauche décrit l'ensemble du processus et le fragment de code à droite contient des sous-programmes pour la quantification secondaire et la recherche de valeurs aberrantes :
# 🎜🎜##🎜 🎜#EXPERIMENT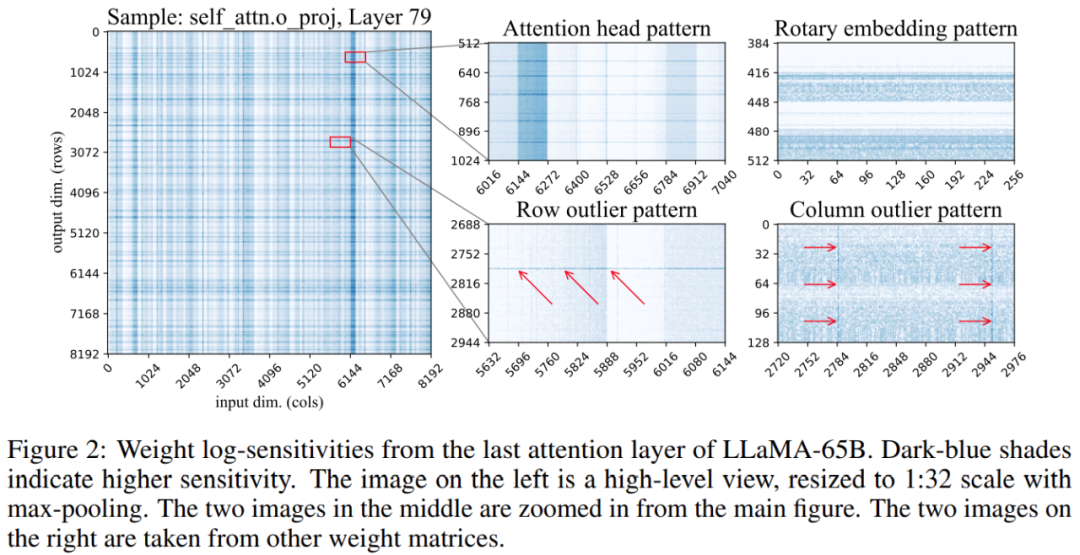
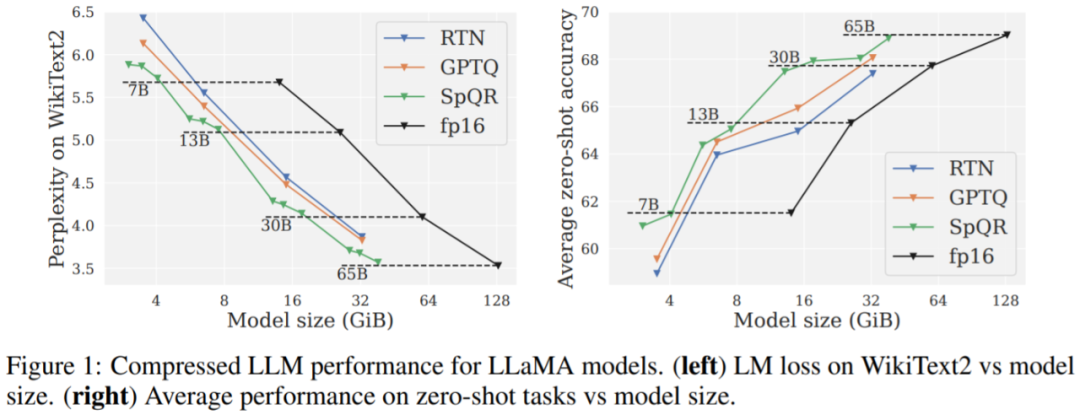
Principaux résultats. Les résultats de la figure 1 montrent qu'à des tailles de modèle similaires, SpQR fonctionne nettement mieux que GPTQ (et le RTN correspondant), en particulier sur les modèles plus petits. Cette amélioration est due au fait que SpQR atteint plus de compression tout en réduisant également la dégradation des pertes.
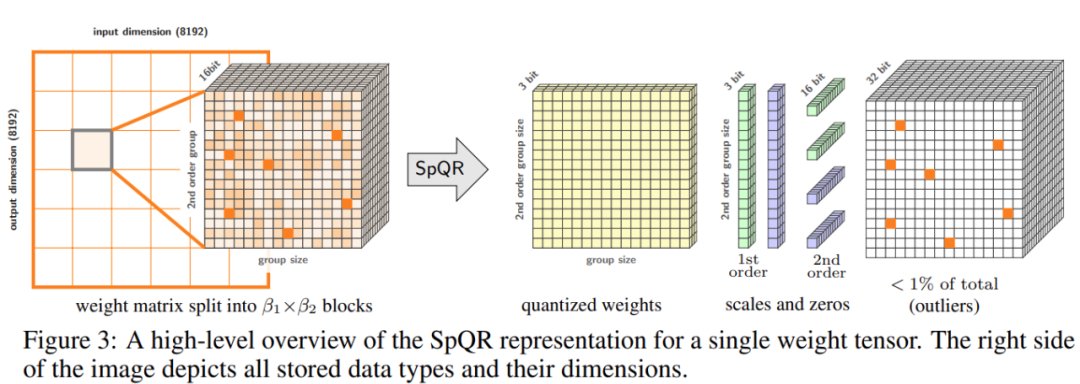
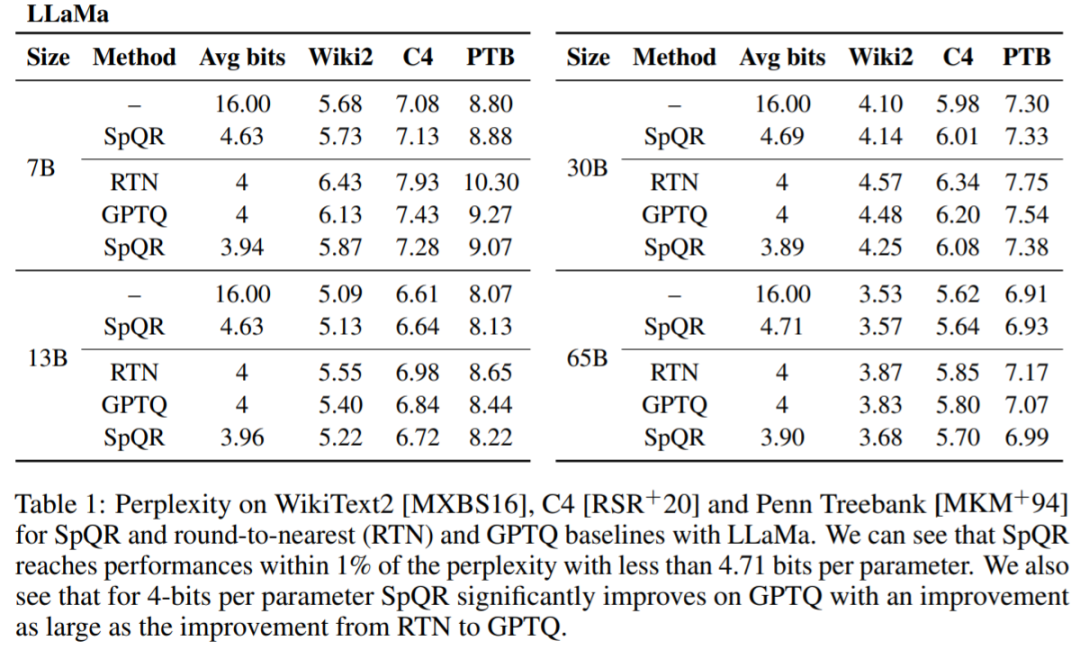
Tableau 1, Tableau 2 Les résultats montrent que pour une quantification 4 bits, SpQR est meilleur que GPTQ avec respect à 16 L'erreur dans la ligne de base des bits est réduite de moitié.

# 🎜 🎜#Le Tableau 3 rapporte les résultats de perplexité du modèle LLaMA-65B sur différents ensembles de données.
Enfin, l'étude évalue la vitesse d'inférence SpQR. Cette étude compare un algorithme de multiplication matricielle clairsemée spécialement conçu avec l'algorithme implémenté dans PyTorch (cuSPARSE), et les résultats sont présentés dans le tableau 4. Comme vous pouvez le voir, bien que la multiplication matricielle clairsemée standard dans PyTorch ne soit pas plus rapide que l'inférence 16 bits, l'algorithme de multiplication matricielle clairsemée spécialement conçu dans cet article peut améliorer la vitesse d'environ 20 à 30 %.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Le modèle MoE open source le plus puissant au monde est ici, avec des capacités chinoises comparables à celles du GPT-4, et le prix ne représente que près d'un pour cent de celui du GPT-4-Turbo.
May 07, 2024 pm 04:13 PM
Le modèle MoE open source le plus puissant au monde est ici, avec des capacités chinoises comparables à celles du GPT-4, et le prix ne représente que près d'un pour cent de celui du GPT-4-Turbo.
May 07, 2024 pm 04:13 PM
Imaginez un modèle d'intelligence artificielle qui non seulement a la capacité de surpasser l'informatique traditionnelle, mais qui permet également d'obtenir des performances plus efficaces à moindre coût. Ce n'est pas de la science-fiction, DeepSeek-V2[1], le modèle MoE open source le plus puissant au monde est ici. DeepSeek-V2 est un puissant mélange de modèle de langage d'experts (MoE) présentant les caractéristiques d'une formation économique et d'une inférence efficace. Il est constitué de 236B paramètres, dont 21B servent à activer chaque marqueur. Par rapport à DeepSeek67B, DeepSeek-V2 offre des performances plus élevées, tout en économisant 42,5 % des coûts de formation, en réduisant le cache KV de 93,3 % et en augmentant le débit de génération maximal à 5,76 fois. DeepSeek est une entreprise explorant l'intelligence artificielle générale
 KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
Plus tôt ce mois-ci, des chercheurs du MIT et d'autres institutions ont proposé une alternative très prometteuse au MLP – KAN. KAN surpasse MLP en termes de précision et d’interprétabilité. Et il peut surpasser le MLP fonctionnant avec un plus grand nombre de paramètres avec un très petit nombre de paramètres. Par exemple, les auteurs ont déclaré avoir utilisé KAN pour reproduire les résultats de DeepMind avec un réseau plus petit et un degré d'automatisation plus élevé. Plus précisément, le MLP de DeepMind compte environ 300 000 paramètres, tandis que le KAN n'en compte qu'environ 200. KAN a une base mathématique solide comme MLP est basé sur le théorème d'approximation universelle, tandis que KAN est basé sur le théorème de représentation de Kolmogorov-Arnold. Comme le montre la figure ci-dessous, KAN a
 Les robots Tesla travaillent dans les usines, Musk : Le degré de liberté des mains atteindra 22 cette année !
May 06, 2024 pm 04:13 PM
Les robots Tesla travaillent dans les usines, Musk : Le degré de liberté des mains atteindra 22 cette année !
May 06, 2024 pm 04:13 PM
La dernière vidéo du robot Optimus de Tesla est sortie, et il peut déjà fonctionner en usine. À vitesse normale, il trie les batteries (les batteries 4680 de Tesla) comme ceci : Le responsable a également publié à quoi cela ressemble à une vitesse 20 fois supérieure - sur un petit "poste de travail", en sélectionnant et en sélectionnant et en sélectionnant : Cette fois, il est publié L'un des points forts de la vidéo est qu'Optimus réalise ce travail en usine, de manière totalement autonome, sans intervention humaine tout au long du processus. Et du point de vue d'Optimus, il peut également récupérer et placer la batterie tordue, en se concentrant sur la correction automatique des erreurs : concernant la main d'Optimus, le scientifique de NVIDIA Jim Fan a donné une évaluation élevée : la main d'Optimus est l'un des robots à cinq doigts du monde. le plus adroit. Ses mains ne sont pas seulement tactiles
 Surpassant largement le DPO : l'équipe de Chen Danqi a proposé une optimisation simple des préférences SimPO et a également affiné le modèle open source 8B le plus puissant.
Jun 01, 2024 pm 04:41 PM
Surpassant largement le DPO : l'équipe de Chen Danqi a proposé une optimisation simple des préférences SimPO et a également affiné le modèle open source 8B le plus puissant.
Jun 01, 2024 pm 04:41 PM
Afin d'aligner les grands modèles de langage (LLM) sur les valeurs et les intentions humaines, il est essentiel d'apprendre les commentaires humains pour garantir qu'ils sont utiles, honnêtes et inoffensifs. En termes d'alignement du LLM, une méthode efficace est l'apprentissage par renforcement basé sur le retour humain (RLHF). Bien que les résultats de la méthode RLHF soient excellents, certains défis d’optimisation sont impliqués. Cela implique de former un modèle de récompense, puis d'optimiser un modèle politique pour maximiser cette récompense. Récemment, certains chercheurs ont exploré des algorithmes hors ligne plus simples, dont l’optimisation directe des préférences (DPO). DPO apprend le modèle politique directement sur la base des données de préférence en paramétrant la fonction de récompense dans RLHF, éliminant ainsi le besoin d'un modèle de récompense explicite. Cette méthode est simple et stable
 Aucune donnée OpenAI requise, rejoignez la liste des grands modèles de code ! UIUC publie StarCoder-15B-Instruct
Jun 13, 2024 pm 01:59 PM
Aucune donnée OpenAI requise, rejoignez la liste des grands modèles de code ! UIUC publie StarCoder-15B-Instruct
Jun 13, 2024 pm 01:59 PM
À la pointe de la technologie logicielle, le groupe de l'UIUC Zhang Lingming, en collaboration avec des chercheurs de l'organisation BigCode, a récemment annoncé le modèle de grand code StarCoder2-15B-Instruct. Cette réalisation innovante a permis une percée significative dans les tâches de génération de code, dépassant avec succès CodeLlama-70B-Instruct et atteignant le sommet de la liste des performances de génération de code. Le caractère unique de StarCoder2-15B-Instruct réside dans sa stratégie d'auto-alignement pur. L'ensemble du processus de formation est ouvert, transparent et complètement autonome et contrôlable. Le modèle génère des milliers d'instructions via StarCoder2-15B en réponse au réglage fin du modèle de base StarCoder-15B sans recourir à des annotations manuelles coûteuses.
 Le LLM est terminé ! OmniDrive : Intégration de la perception 3D et de la planification du raisonnement (la dernière version de NVIDIA)
May 09, 2024 pm 04:55 PM
Le LLM est terminé ! OmniDrive : Intégration de la perception 3D et de la planification du raisonnement (la dernière version de NVIDIA)
May 09, 2024 pm 04:55 PM
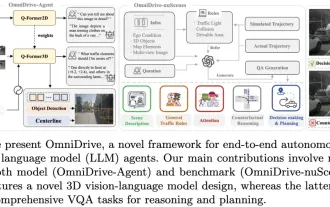
Écrit ci-dessus et compréhension personnelle de l'auteur : cet article est dédié à la résolution des principaux défis des grands modèles de langage multimodaux (MLLM) actuels dans les applications de conduite autonome, c'est-à-dire le problème de l'extension des MLLM de la compréhension 2D à l'espace 3D. Cette expansion est particulièrement importante car les véhicules autonomes (VA) doivent prendre des décisions précises concernant les environnements 3D. La compréhension spatiale 3D est essentielle pour les véhicules utilitaires car elle a un impact direct sur la capacité du véhicule à prendre des décisions éclairées, à prédire les états futurs et à interagir en toute sécurité avec l’environnement. Les modèles de langage multimodaux actuels (tels que LLaVA-1.5) ne peuvent souvent gérer que des entrées d'images de résolution inférieure (par exemple) en raison des limitations de résolution de l'encodeur visuel et des limitations de la longueur de la séquence LLM. Cependant, les applications de conduite autonome nécessitent
 Comparaison des performances de différents frameworks Java
Jun 05, 2024 pm 07:14 PM
Comparaison des performances de différents frameworks Java
Jun 05, 2024 pm 07:14 PM
Comparaison des performances de différents frameworks Java : Traitement des requêtes API REST : Vert.x est le meilleur, avec un taux de requêtes de 2 fois SpringBoot et 3 fois Dropwizard. Requête de base de données : HibernateORM de SpringBoot est meilleur que l'ORM de Vert.x et Dropwizard. Opérations de mise en cache : le client Hazelcast de Vert.x est supérieur aux mécanismes de mise en cache de SpringBoot et Dropwizard. Cadre approprié : choisissez en fonction des exigences de l'application. Vert.x convient aux services Web hautes performances, SpringBoot convient aux applications gourmandes en données et Dropwizard convient à l'architecture de microservices.
 Yolov10 : explication détaillée, déploiement et application en un seul endroit !
Jun 07, 2024 pm 12:05 PM
Yolov10 : explication détaillée, déploiement et application en un seul endroit !
Jun 07, 2024 pm 12:05 PM
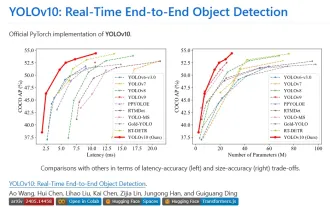
1. Introduction Au cours des dernières années, les YOLO sont devenus le paradigme dominant dans le domaine de la détection d'objets en temps réel en raison de leur équilibre efficace entre le coût de calcul et les performances de détection. Les chercheurs ont exploré la conception architecturale de YOLO, les objectifs d'optimisation, les stratégies d'expansion des données, etc., et ont réalisé des progrès significatifs. Dans le même temps, le recours à la suppression non maximale (NMS) pour le post-traitement entrave le déploiement de bout en bout de YOLO et affecte négativement la latence d'inférence. Dans les YOLO, la conception de divers composants manque d’une inspection complète et approfondie, ce qui entraîne une redondance informatique importante et limite les capacités du modèle. Il offre une efficacité sous-optimale et un potentiel d’amélioration des performances relativement important. Dans ce travail, l'objectif est d'améliorer encore les limites d'efficacité des performances de YOLO à la fois en post-traitement et en architecture de modèle. à cette fin





