
Qui aurait pensé que la « volonté » d'un étudiant de ne pas vouloir passer un examen affecterait plus tard l'ensemble d'Internet.
Dans un cours de théorie de l'information au MIT il y a 70 ans, un enseignant posait une question à choix multiples afin de « réduire » le stress des élèves.
Soit passez l'examen final, soit rédigez un article pour améliorer l'algorithme existant, votre choix.
Le professeur s’appelait Robert Fanno. Ce qu’il n’a pas dit aux élèves, c’est que cet « algorithme existant » était exactement le Shannon-Fanno coding qu’il a co-écrit avec Shannon, le fondateur de la théorie de l’information. Afin de combler les lacunes de l'algorithme, il a lui-même investi beaucoup de temps dans la recherche.
(OS interne de l'enseignant : je ne m'attendais pas à cela.)
Même si c'est un peu dommageable, cette astuce fonctionne vraiment. Ce groupe d'étudiants n'a pas eu besoin de passer l'examen dès qu'ils ont entendu « remettre un devoir » et ont décidé d'écrire un devoir après s'être gratté la tête, y compris David Huffman.
Vous ne saurez pas si vous ne choisissez pas, mais vous serez choqué si vous choisissez. Huffman, qui venait tout juste de débuter, s'est vite rendu compte du piège que l'enseignant avait creusé : ce document était trop difficile à résoudre.
Il a fallu plusieurs mois pour écrire ceci, et malgré le travail acharné, Huffman n'a toujours rien obtenu.
Mais le destin est parfois très étrange. Juste au moment où Huffman a finalement renoncé à « sauter l'examen » et était sur le point de jeter les notes papier à la poubelle, il a soudainement eu une idée ! La réponse apparaît !
Huffman a abandonné la recherche sur le codage existant et s'est tourné vers de nouvelles explorations, et a finalement découvert une méthode basée sur le codage d'arbre binaire à fréquence ordonnée.
L'efficacité de cette idée qu'il a proposée a surpassé avec succès la méthodologie de son professeur. Même dans le développement ultérieur, la méthode de codage qui porte son nom - Codage Huffman, a directement changé le paradigme de compression de données.
Quant au rapport final de l'époque, il a été cité près de 10 000 fois.
En 1951, Robert Fanno, qui enseignait au MIT, réfléchissait à un problème difficile en théorie de l'information :
Comment utiliser le code binaire efficacement pour représenter des chiffres, des lettres ou d'autres symboles ?
La méthode la plus courante et la plus directe à l'époque consistait à attribuer un nombre binaire unique à chaque caractère.
Par exemple, la lettre A peut être représentée par 01000001, ! Représenté par 00100001, chaque nombre à huit chiffres correspond à un caractère.
Cela rend le code facile à analyser, mais l'efficacité est extrêmement faible.
Il existe également une méthode d'optimisation, similaire au code Morse. La lettre commune E est représentée par juste un point, mais la lettre rare Q nécessite un "————·——" plus long et plus laborieux.
Cette méthode entraînera des longueurs de code différentes et les informations ne seront pas faciles à comprendre. De plus, des espaces doivent être ajoutés entre les caractères lors de la transmission, sinon différentes combinaisons de caractères ne pourront pas être distinguées.
Fanno s'est rendu compte que peut-être les avantages de ces deux méthodes pourraient être combinés - représenter des caractères dans des codes binaires de différentes longueurs. De plus, afin d'éviter le "chevauchement" du code, il a également construit un arbre binaire.
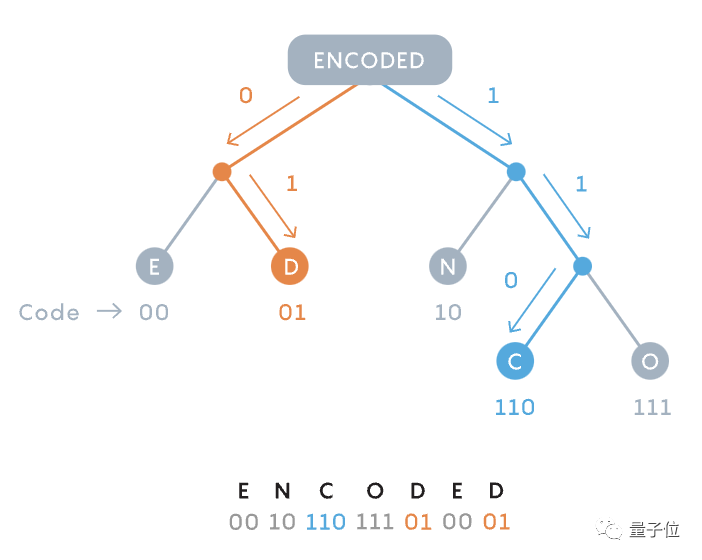 Photos
Photos
Il a testé de manière exhaustive la possibilité de chaque permutation pour une efficacité maximale, et a finalement obtenu une situation efficace :
Chaque message est divisé en deux branches selon la fréquence, et autant que possible Laissez la fréquence de l'utilisation des lettres des deux côtés est fondamentalement la même.
 Images
Images
Codage Shannon-Fano.
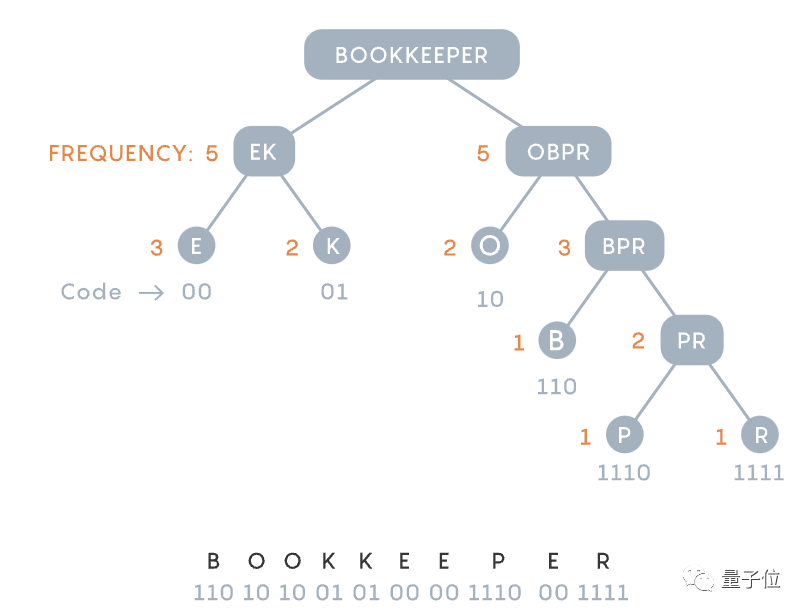
Mais cette méthode ne fonctionne pas toujours. Par exemple, lorsque la probabilité d'apparition de lettres est {0,35, 0,17, 0,17, 0,16, 0,15}, le codage idéal ne peut pas être donné. Fano estime qu'il doit y avoir une meilleure stratégie de compression. Depuis lors, une tâche aussi importante a été confiée à ses étudiants. Un éclair d'inspiration, un article du siècleEn fait, la méthode du professeur Fanno consiste à construire un arbre de caractères de haut en bas et à maintenir autant de symétrie que possible entre les paires de branches. Ensuite, la méthode de Huffman renverse directement ce processus -Construisez un arbre binaire de bas en haut.
Il pensait que quoi qu'il arrive, dans un morceau de code valide, lesdeux caractères les moins courants devraient avoir les deux codes les plus longs.
Alors identifiez d'abord les deux caractères les moins communs, combinez-les ensemble pour former une paire de branches, puis répétez le processus pour trouver le caractère le moins commun parmi les caractères restants et la paire de caractères que vous venez de construire (paire).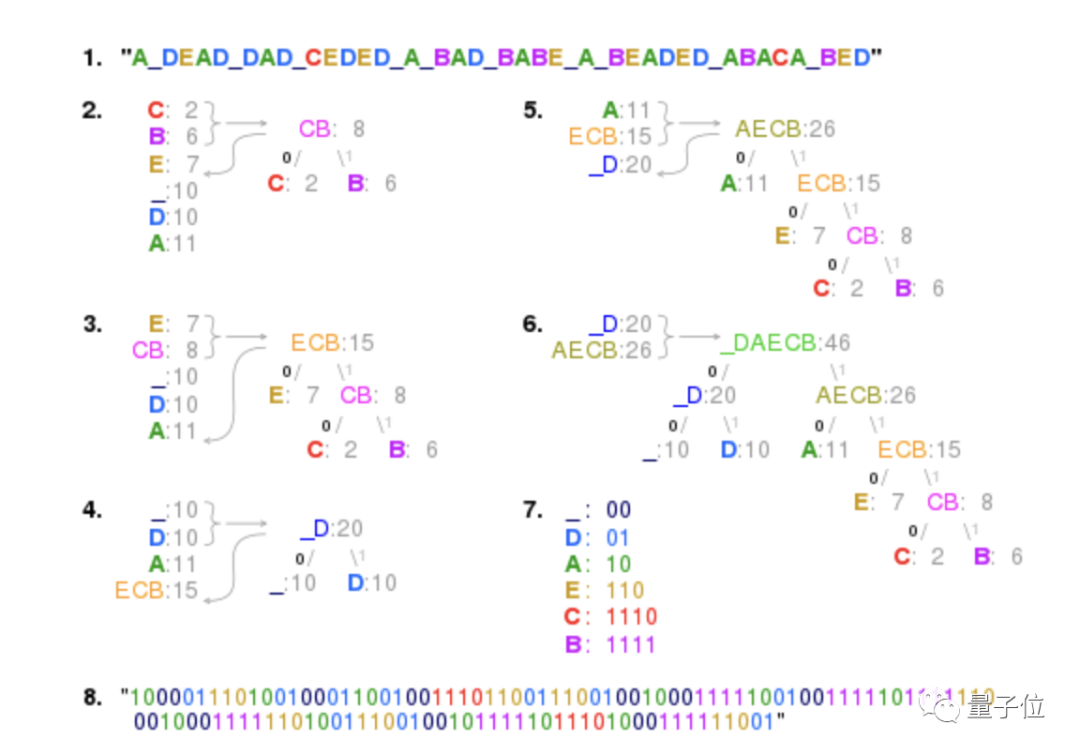 Image
Image
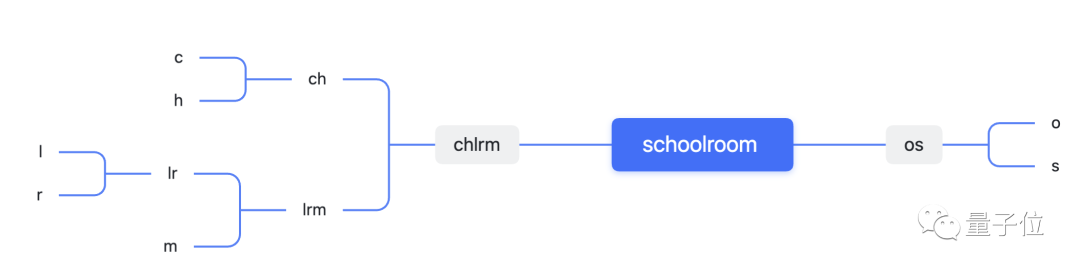
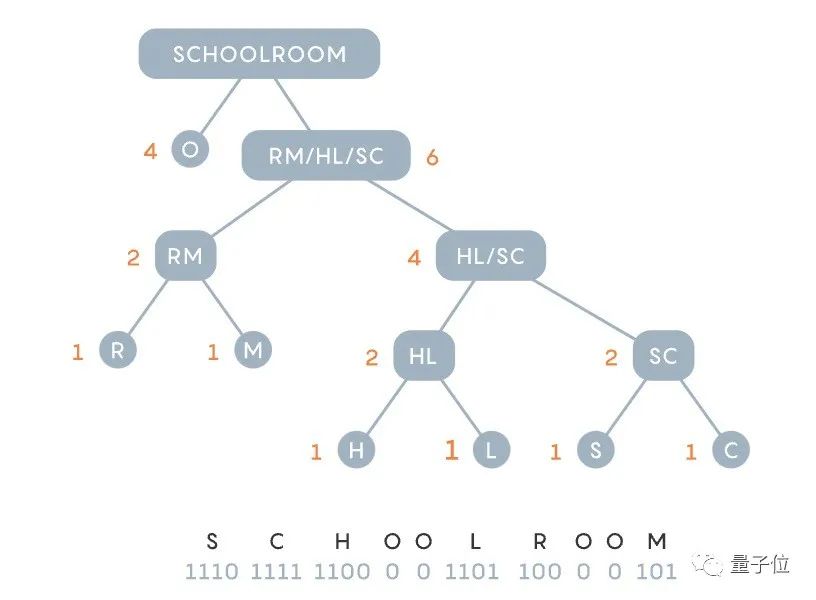
Prenons salle d'école comme exemple, où O apparaît quatre fois et S, C, H, L, R et M apparaissent une fois chacun.
La méthode de Fano consiste à attribuer d'abord O et une autre lettre à la branche gauche, de sorte que les deux côtés aient une utilisation totale de 5 fois et que le code généré totalise 27 bits.
 Images
Images
En revanche, la méthode de Huffman, par exemple, part des r et m rares et les combine en une paire de lettres.
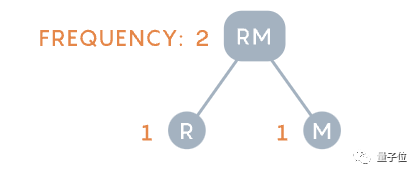 Images
Images
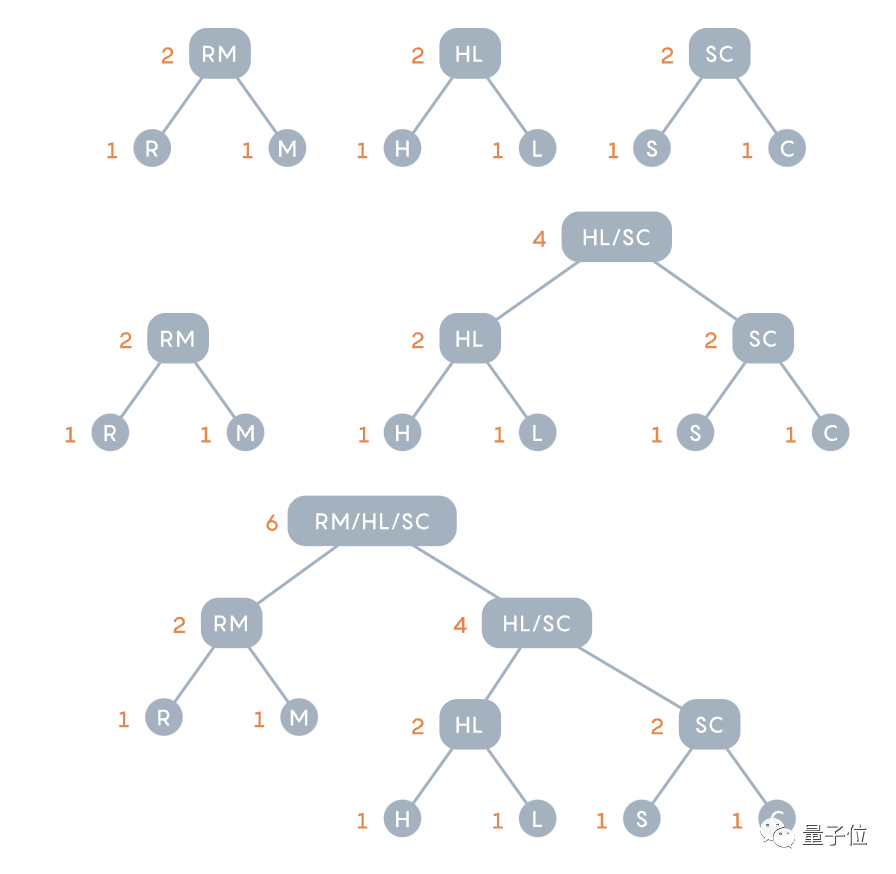
Après la combinaison, les caractères existants (paires) comprennent : O (4 fois), RM (2 fois) et les lettres simples S, C, H et L.
Divisez en fonction de la fréquence d'occurrence, répétez l'opération précédente - regroupez les deux options peu courantes, puis mettez à jour l'arbre numérique et le diagramme de fréquence.
Finalement, « salle de classe » est devenu 11101111110000110110000101, 1 peu de moins que l'approche descendante de Fano.
 Photo
Photo
Bien qu'un bit ne représente pas grand-chose ici, lorsqu'il est étendu à des milliards d'octets, cela représente une grosse économie.
En fait, la méthode de Huffman s'est avérée très puissante. Selon les statistiques de Google Scholar, l'article a été cité cette année-là 9 570 fois.
 Photos
Photos
Quant à la méthode de son professeur, elle n’a quasiment plus jamais été utilisée.
À ce jour, presque toutes les méthodes de compression sans perte utilisent la méthode de Huffman en tout ou en partie, qui peut compresser des images, de l'audio, des tableaux, etc. Il prend en charge tout, du standard d'image PNG au logiciel omniprésent PKZip.
Knuth, pionnier de l'informatique moderne et lauréat du prix Turing, a un jour décrit ainsi les réalisations de Huffman :
Dans les domaines de l'informatique et des communications de données, le codage de Huffman est une idée de base que les gens utilisent.
Plus tard, Huffman a rappelé ce moment « eurêka », à ce moment-là, il était sur le point de jeter les notes papier dans la poubelle, mais soudain ses pensées se sont réunies et la réponse est apparue dans son esprit :
C'était le plus étrange. chose dans ma vie.
Illumination soudaine, comme un éclair.
Et a déclaré que s'il avait su que son professeur Fano avait été aux prises avec ce problème, il n'aurait peut-être jamais essayé de le résoudre, et encore moins de franchir le pas à l'âge de 25 ans.
Le codage de Huffman a changé le paradigme de la compression des données et a remporté de nombreux honneurs et médailles pour cela.
Par exemple, Huffman a remporté le Golden Jubilee Award for Technical Innovation de l'IEEE Information Theory Society en 1998 et la médaille Richard Hamming de l'Institute of Electrical and Electronics Engineers (IEEE) en 1999.
Mais malgré tout, au cours de sa vie, par rapport à l'invention de la méthode de compression sans perte, ce dont il était le plus fier était cette thèse de doctorat.
Titre : La synthèse des circuits de commutation séquentielle.
 Photo
Photo
Alors que Huffman étudiait pour son doctorat au MIT, il a publié cet article important sur les circuits de commutation séquentielle. À cette époque, Huffman était presque le premier chercheur à expliquer comment concevoir un circuit de commutation séquentielle asynchrone. Cette théorie a ensuite fourni un support logique important pour le développement des ordinateurs. La publication de cet article l'a non seulement aidé à obtenir la médaille Louis E. Levy du Franklin Institute, mais lui a aussi naturellement permis d'obtenir la qualification pour rester à l'école et donner des cours sur les circuits de commutation.
Photos Pendant ses études, Huffman a également proposé une formule mathématique innovante qui peut convertir une
Pendant ses études, Huffman a également proposé une formule mathématique innovante qui peut convertir une
sans perdre aucune information. Cette recherche a joué un rôle important à l'époque et lui a valu. un poste important. William O. Baker, alors vice-président de la recherche chez Bell Labs, l'a recruté dans un comité d'examen principalement chargé d'examiner les futurs plans technologiques de la National Security Agency. Le Dr Baker a été conseiller scientifique auprès de cinq présidents : Eisenhower, Kennedy, Johnson, Nixon et Reagan. En 1967, Hoffman, qui était déjà professeur titulaire, choisit de quitter le MIT et de rejoindre l'Université de Californie à Santa Cruz (UCSC). Durant cette période, il dirigea la création du Département d'informatique. La science et a participé à l'élaboration de cours académiques, jetant les bases de l'informatique future, une base importante pour le développement du système. On peut dire que les mathématiques sont l’une des activités de toute une vie de Huffman, à tel point que lorsqu’il s’est ensuite engagé dans l’art, il ne pouvait plus se passer des mathématiques. À partir des années 1970, Huffman s'est intéressé à l'origami, alors qu'il étudiait les mathématiques et l'art de l'origami. a créé des centaines d'œuvres d'origami et publié un article analysant les propriétés mathématiques de l'origami , devenant ainsi un pionnier dans le domaine des mathématiques de l'origami. Avec le recul, Huffman a remporté d'innombrables honneurs et distinctions dans sa vie, mais il n'a jamais rien fait pour lui-même . Une invention a été brevetée. Enfin, permettez-moi d'emprunter une citation de Huffman lui-même. En tant que scientifique et enseignant, je suis vraiment persévérant. Si je sens que je n'ai pas trouvé la solution la plus simple à un problème, je deviens extrêmement insatisfait, et cette insatisfaction continuera jusqu'à ce que je trouve la meilleure solution. Pour moi, c’est l’essence même du métier de scientifique.  Picture
Picture

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Logiciel d'édition de pages Web
Logiciel d'édition de pages Web
 Solution à 0x84b10001
Solution à 0x84b10001
 Quelles sont les vulnérabilités courantes de Tomcat ?
Quelles sont les vulnérabilités courantes de Tomcat ?
 Comment ouvrir le fichier apk
Comment ouvrir le fichier apk
 ps ajuster les touches de raccourci du bord
ps ajuster les touches de raccourci du bord
 l'utilisation du processeur
l'utilisation du processeur
 Impossible de démarrer votre ordinateur normalement
Impossible de démarrer votre ordinateur normalement
 outils de développement Python
outils de développement Python
 exception nullpointerexception
exception nullpointerexception