php二分查找二种实现示例_PHP
php二分查找示例
二分查找常用写法有递归和非递归,在寻找中值的时候,可以用插值法代替求中值法。
当有序数组中的数据均匀递增时,采用插值方法可以将算法复杂度从中值法的lgN减小到lglgN
复制代码 代码如下:
/**
* 二分查找递归解法
* @param type $subject
* @param type $start
* @param type $end
* @param type $key
* @return boolean
*/
function binarySearch_r($subject, $start, $end, $key)
{
if ( $start >= $end ) return FALSE;
$mid = getMidKey($subject, $start, $end, $key);
if ( $subject[$mid] == $key ) return $mid;
if ( $key > $subject[$mid] ) {
return binarySearch($subject, $mid, $end, $key);
}
if ( $key return binarySearch($subject, $start, $mid, $key);
}
}
/**
* 二分查找的非递归算法
* @param type $subject
* @param type $n
* @param type $key
*/
function binarySearch_nr($subject, $n, $key)
{
$low = 0;
$high = $n;
while ( $low $mid = getMidKey($subject, $low, $high, $key);
if ( $subject[$mid] == $key ) return $mid;
if ( $subject[$mid] $low = $mid + 1;
}
if ( $subject[$mid] > $key ) {
$high = $mid - 1;
}
}
}
function getMidKey($subject, $low, $high, $key)
{
/**
* 取中值算法1 取中值 不用 ($low+$high)/2的方式是因为 防止low和high较大时候,产生溢出....
*/
//return round($low + ($high - $low) / 2);
/**
* 经过改进的插值算法求中值,当数值分布均匀情况下,再降低算法复杂度到lglgN
* 取中值算法2
*/
return round( (($key - $subject[$low]) / ($subject[$high] - $subject[$low])*($high-$low) ) );
}

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Comment écrire un algorithme de recherche binaire en utilisant C#
Sep 19, 2023 pm 12:42 PM
Comment écrire un algorithme de recherche binaire en utilisant C#
Sep 19, 2023 pm 12:42 PM
Comment utiliser C# pour écrire un algorithme de recherche binaire. L'algorithme de recherche binaire est un algorithme de recherche efficace. Il trouve la position d'un élément spécifique dans un tableau ordonné avec une complexité temporelle de O(logN). En C#, nous pouvons écrire un algorithme de recherche binaire en suivant les étapes suivantes. Étape 1 : Préparer les données Tout d’abord, nous devons préparer un tableau trié comme données cibles pour la recherche. Supposons que nous voulions trouver la position d'un élément spécifique dans un tableau. int[]données={1,3,5,7,9,11,13
 Programme de recherche binaire écrit en langage C, utilisant pthread pour le traitement multi-thread
Aug 26, 2023 pm 12:45 PM
Programme de recherche binaire écrit en langage C, utilisant pthread pour le traitement multi-thread
Aug 26, 2023 pm 12:45 PM
Nous savons que la méthode de recherche binaire est l’algorithme de tri le plus adapté et le plus efficace. Cet algorithme fonctionne sur des séquences triées. L'algorithme est simple, il trouve simplement l'élément du milieu, puis divise la liste en deux parties et se déplace vers la sous-liste de gauche ou la sous-liste de droite. Nous connaissons son algorithme. Nous allons maintenant voir comment utiliser la technique de recherche binaire dans un environnement multi-thread. Le nombre de threads dépend du nombre de cœurs présents dans le système. Jetons un coup d'œil au code pour avoir une idée. Exemple#include<iostream>#defineMAX16#defineMAX_THREAD4usingnamespacestd;//placearr,keyandothervariabl
 Comment implémenter un algorithme de recherche binaire en utilisant Java
Sep 19, 2023 pm 12:57 PM
Comment implémenter un algorithme de recherche binaire en utilisant Java
Sep 19, 2023 pm 12:57 PM
Comment utiliser Java pour implémenter un algorithme de recherche binaire L'algorithme de recherche binaire est une méthode de recherche efficace adaptée aux tableaux triés. Son idée de base est de restreindre continuellement la plage de recherche, de comparer la valeur de recherche avec les éléments du milieu du tableau et de décider s'il faut continuer la recherche dans la moitié gauche ou la moitié droite en fonction du résultat de la comparaison jusqu'à ce que l'élément cible soit trouvé ou la plage de recherche est réduite à vide. Ci-dessous, nous présenterons en détail comment implémenter l'algorithme de recherche binaire en Java. Étape 1 : Implémenter la méthode de recherche binaire publicclassBinarySearch
 Comment implémenter un algorithme de recherche binaire en utilisant Python ?
Sep 20, 2023 pm 01:24 PM
Comment implémenter un algorithme de recherche binaire en utilisant Python ?
Sep 20, 2023 pm 01:24 PM
Comment implémenter un algorithme de recherche binaire en utilisant Python ? L'algorithme de recherche binaire, également connu sous le nom d'algorithme de recherche binaire, est un algorithme de recherche efficace. Il fonctionne sur des tableaux ou des listes ordonnés, en limitant la recherche en comparant la valeur cible aux éléments au milieu du tableau. Ce qui suit présentera comment implémenter l'algorithme de recherche binaire en Python et fournira des exemples de code spécifiques. Idée d'algorithme : comparez la valeur cible avec l'élément du milieu du tableau ; s'ils sont égaux, renvoyez la position de l'élément si la valeur cible est supérieure à l'élément du milieu, alors à droite ;
 Comment trouver le plus petit élément d'un tableau à l'aide d'un algorithme de recherche binaire en langage C ?
Aug 25, 2023 pm 08:37 PM
Comment trouver le plus petit élément d'un tableau à l'aide d'un algorithme de recherche binaire en langage C ?
Aug 25, 2023 pm 08:37 PM
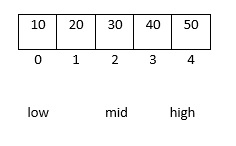
Le langage de programmation C propose deux techniques de recherche. Ils sont les suivants : Recherche linéaire Recherche binaire Recherche binaire Cette méthode ne convient qu'aux listes ordonnées. La liste donnée est divisée en deux parties égales. La clé donnée est comparée à l'élément du milieu de la liste. Ici, trois choses peuvent se produire, comme suit : Si l'élément du milieu correspond au mot-clé, la recherche se terminera avec succès ici. Si l'élément du milieu est plus grand que le mot-clé, la recherche aura lieu dans la partition de gauche. Si l'élément du milieu est plus petit que le mot-clé, la recherche sera effectuée sur la partition de droite. Entrée (i/p) - liste non triée d'éléments, mots-clés. Sortie (o/p)-succès-si échec de la recherche du mot-clé-sinon key=20mid=(low+high)/2 Programme 1 Ce qui suit est l'utilisation de la recherche binaire dans
 Programme Java pour trouver la racine cubique d'un nombre à l'aide d'un algorithme de recherche binaire
Aug 28, 2023 pm 01:33 PM
Programme Java pour trouver la racine cubique d'un nombre à l'aide d'un algorithme de recherche binaire
Aug 28, 2023 pm 01:33 PM
Une racine cubique est une valeur entière qui, multipliée par elle-même trois fois de suite, donne la valeur d'origine. Dans cet article, nous allons écrire un programme Java qui utilise la recherche binaire pour trouver la racine cubique d'un nombre. Trouver la racine cubique d'un nombre est une application de l'algorithme de recherche binaire. Dans cet article, nous verrons en détail comment utiliser la recherche binaire pour calculer les racines cubiques. Exemple d'entrée-sortie Exemple-1 :Input:64Output:4 Par exemple, la racine cubique de 64 est 4 et la sortie est 4. Exemple 2 : Entrée : 216 Sortie : 6 Par exemple, la racine cubique de 216 est 6 et la sortie est 6. Recherche binaire La recherche binaire est un algorithme utilisé pour trouver des éléments (c'est-à-dire des clés dans un tableau trié). Fonctionnement de l'algorithme binaire
 Dans le programme C, utilisez un algorithme de recherche binaire pour rechercher des nombres rationnels sans utiliser l'arithmétique à virgule flottante
Aug 27, 2023 pm 06:05 PM
Dans le programme C, utilisez un algorithme de recherche binaire pour rechercher des nombres rationnels sans utiliser l'arithmétique à virgule flottante
Aug 27, 2023 pm 06:05 PM
Dans ce problème, on nous donne un tableau trié de nombres rationnels. Nous devons utiliser un algorithme de recherche binaire pour rechercher un élément donné de ce tableau de nombres rationnels sans utiliser d'opérations à virgule flottante. Les nombres rationnels sont des nombres exprimés sous la forme p/q, où p et q sont tous deux des nombres entiers. Par exemple, ⅔, ⅕. La recherche binaire est une technique de recherche qui permet de trouver des éléments en regardant au milieu d'un tableau. Utilisé pour rechercher des éléments dans un tableau trié de nombres rationnels à l'aide d'une recherche binaire, où les opérations en virgule flottante ne sont pas autorisées. Nous comparerons le numérateur et le dénominateur pour savoir quel élément est le plus grand ou quel élément est celui à trouver. Exemple Créons un programme pour cela, #include<stdio.h>structRational{ &am
 Analyse d'algorithme PHP : Comment utiliser un algorithme de recherche binaire pour localiser rapidement des éléments dans un tableau ordonné ?
Sep 19, 2023 pm 01:14 PM
Analyse d'algorithme PHP : Comment utiliser un algorithme de recherche binaire pour localiser rapidement des éléments dans un tableau ordonné ?
Sep 19, 2023 pm 01:14 PM
Analyse d'algorithme PHP : Comment utiliser un algorithme de recherche binaire pour localiser rapidement des éléments dans un tableau ordonné ? Présentation : L'algorithme de recherche binaire est un algorithme de recherche efficace qui convient à la recherche d'éléments spécifiques dans un tableau ordonné. Cet article présentera en détail le principe de l'algorithme de recherche binaire et donnera des exemples de code PHP. Principe : L'algorithme de recherche binaire localise rapidement l'élément cible en réduisant de moitié la plage de recherche à plusieurs reprises. Le processus est le suivant : d'abord, limitez la plage de recherche au début et à la fin du tableau ; puis calculez l'index de l'élément du milieu et comparez-le avec l'élément cible ;






