 Périphériques technologiques
Périphériques technologiques
 IA
IA
 La formation de modèles de type GPT est accélérée de 26,5 %. Tsinghua Zhu Jun et d'autres utilisent l'algorithme INT4 pour accélérer la formation des réseaux neuronaux.
La formation de modèles de type GPT est accélérée de 26,5 %. Tsinghua Zhu Jun et d'autres utilisent l'algorithme INT4 pour accélérer la formation des réseaux neuronaux.
La formation de modèles de type GPT est accélérée de 26,5 %. Tsinghua Zhu Jun et d'autres utilisent l'algorithme INT4 pour accélérer la formation des réseaux neuronaux.
Nous savons que la quantification des activations, des poids et des gradients en 4 bits est très utile pour accélérer l'entraînement des réseaux neuronaux. Mais les méthodes de formation 4 bits existantes nécessitent des formats de nombres personnalisés qui ne sont pas pris en charge par le matériel contemporain. Dans cet article, Tsinghua Zhu Jun et al. proposent une méthode de formation Transformer qui utilise l'algorithme INT4 pour implémenter toutes les multiplications matricielles.
Le fait que le modèle soit entraîné rapidement ou non est étroitement lié aux exigences en matière de valeurs d'activation, de poids, de gradients et d'autres facteurs.
La formation aux réseaux neuronaux nécessite une certaine quantité de calcul, et l'utilisation d'algorithmes de faible précision (formation à la quantification complète ou formation FQT) devrait améliorer l'efficacité du calcul et de la mémoire. FQT ajoute des quantificateurs et des déquantificateurs au graphe de calcul original de pleine précision et remplace les opérations coûteuses à virgule flottante par des opérations bon marché à virgule flottante de faible précision.
La recherche sur FQT vise à réduire la précision numérique de l'entraînement tout en réduisant le sacrifice de la vitesse et de la précision de convergence. La précision numérique requise est réduite de FP16 à FP8, INT32+INT8 et INT8+INT5. La formation FP8 est effectuée sur les GPU Nvidia H100 avec le moteur Transformer, ce qui permet une accélération incroyable de la formation Transformer à grande échelle.
Récemment, la précision numérique de l'entraînement a été réduite à 4 bits. Sun et al. ont formé avec succès plusieurs réseaux contemporains avec des activations/poids INT4 et des gradients FP4 ; Chmiel et al. ont proposé un format de nombre logarithmique personnalisé à 4 chiffres qui a encore amélioré la précision. Cependant, ces méthodes de formation 4 bits ne peuvent pas être directement utilisées pour l'accélération car elles nécessitent des formats de nombres personnalisés, qui ne sont pas pris en charge sur le matériel contemporain.
Il existe d'énormes défis d'optimisation dans la formation à un niveau aussi bas que 4 bits. Premièrement, le quantificateur non différentiable de propagation vers l'avant rendra le graphique de la fonction de perte inégal, et l'optimiseur basé sur le gradient peut facilement rester bloqué dans le. minimum local excellent. Deuxièmement, le gradient ne peut être calculé qu’approximativement avec une faible précision. Ce gradient imprécis ralentira le processus d’entraînement et conduira même à un entraînement instable ou divergent.
Cet article propose un nouvel algorithme de formation INT4 pour le populaire réseau neuronal Transformer. Les opérations linéaires coûteuses utilisées pour entraîner les transformateurs peuvent toutes être écrites sous forme de multiplication matricielle (MM). Le formalisme MM permet aux chercheurs de concevoir des quantificateurs plus flexibles. Ce quantificateur se rapproche mieux de la multiplication matricielle FP32 grâce à des structures d'activation, de poids et de gradient spécifiques dans Transformer. Le quantificateur présenté dans cet article profite également des nouvelles avancées en algèbre linéaire numérique stochastique.
 Photos
Photos
Adresse papier : https://arxiv.org/pdf/2306.11987.pdf
La recherche montre que pour la propagation vers l'avant, la principale raison de la diminution de la précision est l'anomalie de la valeur d'activation. . Afin de supprimer cette valeur aberrante, le quantificateur Hadamard est proposé, qui est utilisé pour quantifier la matrice d'activation transformée. Cette transformation est une matrice Hadamard en diagonale par blocs, qui répartit les informations portées par les valeurs aberrantes vers les entrées de la matrice proches des valeurs aberrantes, réduisant ainsi la plage numérique des valeurs aberrantes.
Pour la rétropropagation, l'étude profite de la rareté structurelle du gradient d'activation. La recherche montre que les gradients de certains jetons sont très grands, mais en même temps, les gradients de la plupart des autres jetons sont très petits, et même les résidus quantifiés des gradients plus grands sont plus petits. Par conséquent, au lieu de calculer ces petits gradients, les ressources informatiques sont utilisées pour calculer les résidus de gradients plus importants.
Combinant les techniques de quantification de propagation avant et arrière, cet article propose un algorithme qui utilise les MM INT4 pour toutes les opérations linéaires dans Transformer. L'étude a évalué des algorithmes pour former Transformer à diverses tâches, notamment la compréhension du langage naturel, la réponse aux questions, la traduction automatique et la classification d'images. L'algorithme proposé atteint une précision comparable ou meilleure par rapport aux efforts de formation 4 bits existants. De plus, l'algorithme est compatible avec le matériel contemporain (tel que les GPU) puisqu'il ne nécessite pas de formats de nombres personnalisés (tels que les formats FP4 ou logarithmiques). Et le prototype de quantification + opérateur INT4 MM proposé par l'étude est 2,2 fois plus rapide que la référence FP16 MM, augmentant la vitesse d'entraînement de 35,1 %.
Propagation vers l'avant
Au cours du processus de formation, les chercheurs ont utilisé l'algorithme INT4 pour accélérer tous les opérateurs linéaires et définir tous les opérateurs non linéaires à faible intensité de calcul au format FP16. Tous les opérateurs linéaires de Transformer peuvent être écrits sous forme de multiplication matricielle. À des fins de démonstration, ils ont considéré une simple accélération de multiplication matricielle comme suit.
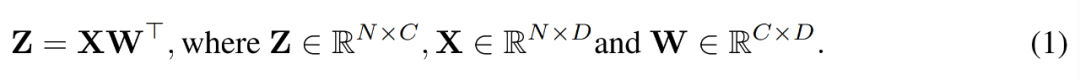 Picture
Picture
Le principal cas d'utilisation de ce type de multiplication matricielle est la couche entièrement connectée.
Quantisation de la taille des pas apprise
La formation accélérée doit utiliser des opérations sur des nombres entiers pour calculer la propagation vers l'avant. Par conséquent, les chercheurs ont utilisé le quantificateur de taille de pas appris (LSQ). En tant que méthode de quantification statique, l'échelle de quantification du LSQ ne dépend pas de l'entrée et est donc moins coûteuse que les méthodes de quantification dynamique. En revanche, les méthodes de quantification dynamique nécessitent de calculer dynamiquement l'échelle de quantification à chaque itération.
Étant donné une matrice FP X, LSQ quantifie X en un entier grâce à la formule suivante (2).
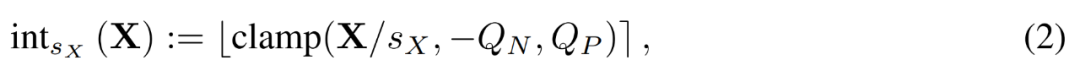 Photos
Photos
Activation des valeurs aberrantes
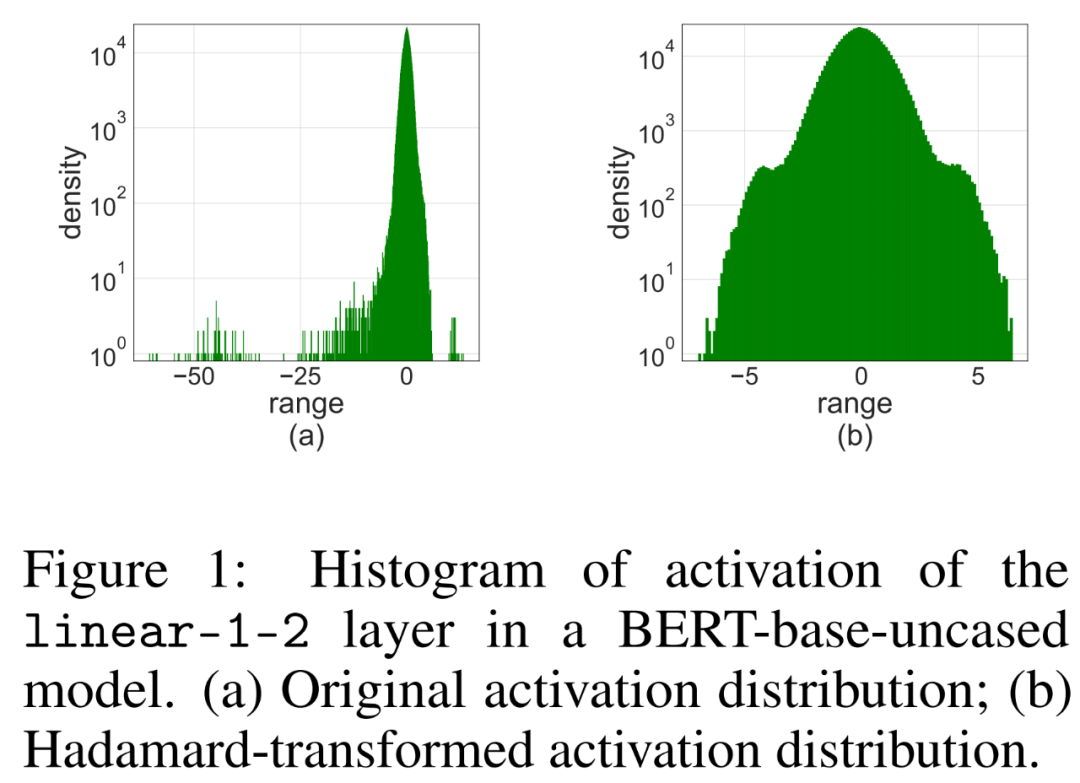
La simple application de LSQ à FQT (entraînement entièrement quantifié, entraînement entièrement quantifié) avec une activation/poids de 4 bits provoquera une activation des valeurs aberrantes en raison d'une diminution de précision. Comme le montre la figure 1 (a) ci-dessous, certains termes aberrants sont activés, dont l'ampleur est beaucoup plus grande que celle des autres termes.
Dans ce cas, la taille du pas s_X est un compromis entre la granularité de quantification et la plage de valeurs représentables. Si s_X est grand, les valeurs aberrantes peuvent être bien représentées au prix d'une représentation grossière de la plupart des autres termes. Si s_X est petit, les termes en dehors de la plage [−Q_Ns_X, Q_Ps_X] doivent être tronqués.
Quantification Hadamard
Les chercheurs ont proposé d'utiliser le quantificateur Hadamard (HQ) pour résoudre le problème des valeurs aberrantes. Son idée principale est de quantifier la matrice dans un autre espace linéaire avec moins de valeurs aberrantes.
Les valeurs aberrantes dans la matrice d'activation peuvent former des structures au niveau des fonctionnalités. Ces valeurs aberrantes sont généralement regroupées selon quelques dimensions, c'est-à-dire que seules quelques colonnes de X sont nettement plus grandes que les autres. En tant que transformation linéaire, la transformée d'Hadamard peut propager des valeurs aberrantes entre autres termes. Plus précisément, la transformée de Hadamard H_k est une matrice 2^k × 2^k.
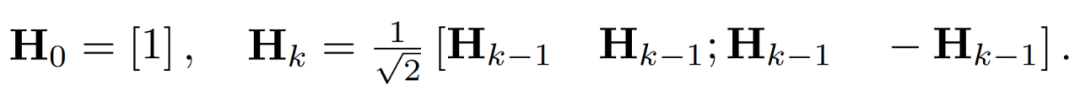
Pour supprimer les valeurs aberrantes, les chercheurs quantifient les versions transformées de X et W.
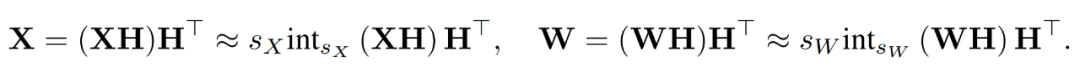
En combinant les matrices quantifiées, le chercheur a obtenu ce qui suit.
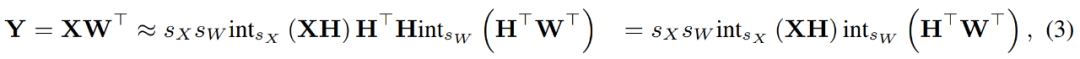
où les transformations inverses s'annulent, et MM peut être implémenté comme suit.
 Images
Images
Rétropropagation
Les chercheurs utilisent les opérations INT4 pour accélérer la rétropropagation des couches linéaires. L'opérateur linéaire HQ-MM défini dans l'équation (3) a quatre entrées, à savoir l'activation X, le poids W et les étapes s_X et s_W. Étant donné le gradient de sortie ∇_YL par rapport à la fonction de perte L, ils doivent calculer les gradients de ces quatre entrées.
Parsemité structurelle des gradients
Les chercheurs ont remarqué que la matrice de gradient ∇_Y est souvent très clairsemée pendant le processus de formation. La structure de parcimonie est telle que quelques lignes (c'est-à-dire les jetons) de ∇_Y ont de grands termes, tandis que la plupart des autres lignes sont proches de vecteurs entièrement nuls. Ils ont tracé un histogramme de la norme par ligne ∥(∇_Y)_i:∥ pour toutes les lignes de la figure 2 ci-dessous.
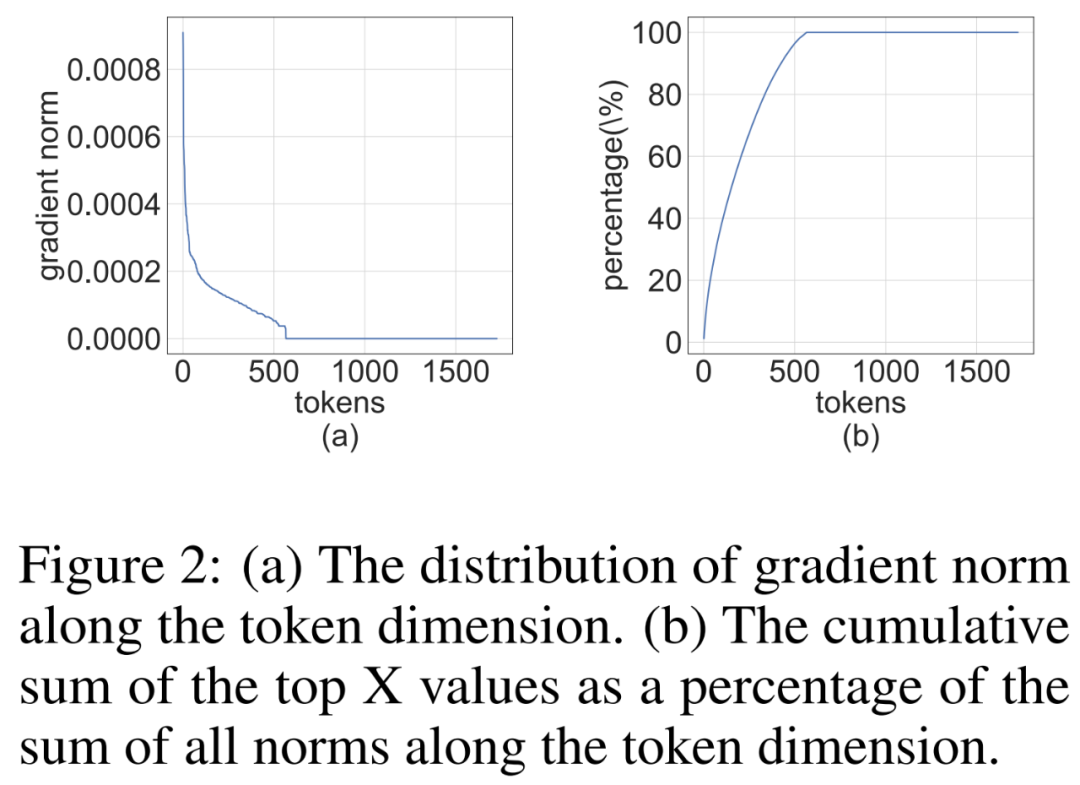 Photos
Photos
Répartition des bits et échantillonnage du score moyen
Les chercheurs discutent de la manière de concevoir des quantificateurs de gradient pour exploiter la rareté structurelle afin de calculer avec précision le MM lors de la rétropropagation. L'idée générale est que le gradient de nombreuses lignes est très petit, donc l'impact sur le gradient des paramètres est également faible, mais de nombreux calculs sont gaspillés. De plus, les grandes lignes ne peuvent pas être représentées avec précision par INT4.
Pour profiter de cette rareté, les chercheurs proposent le fractionnement des bits, qui divise le gradient de chaque jeton en 4 bits supérieurs et 4 bits inférieurs. Ensuite, le gradient contenant le plus d'informations est sélectionné par échantillonnage de scores moyens, qui est une technique d'échantillonnage par importance de RandNLA.
Résultats expérimentaux
L'étude a évalué l'algorithme de formation INT4 sur diverses tâches, notamment le réglage fin du modèle de langage, la traduction automatique et la classification d'images. L'étude a mis en œuvre les algorithmes proposés HQ-MM et LSS-MM à l'aide de CUDA et cutlass2. En plus d'utiliser simplement LSQ comme couche d'intégration, nous avons remplacé tous les opérateurs linéaires à virgule flottante par INT4 et conservé la précision totale du classificateur de dernière couche. Et ce faisant, les chercheurs ont adopté des architectures, des optimiseurs, des planificateurs et des hyperparamètres par défaut pour tous les modèles évalués.
Précision du modèle convergé. Le tableau 1 ci-dessous montre la précision du modèle convergé sur chaque tâche.
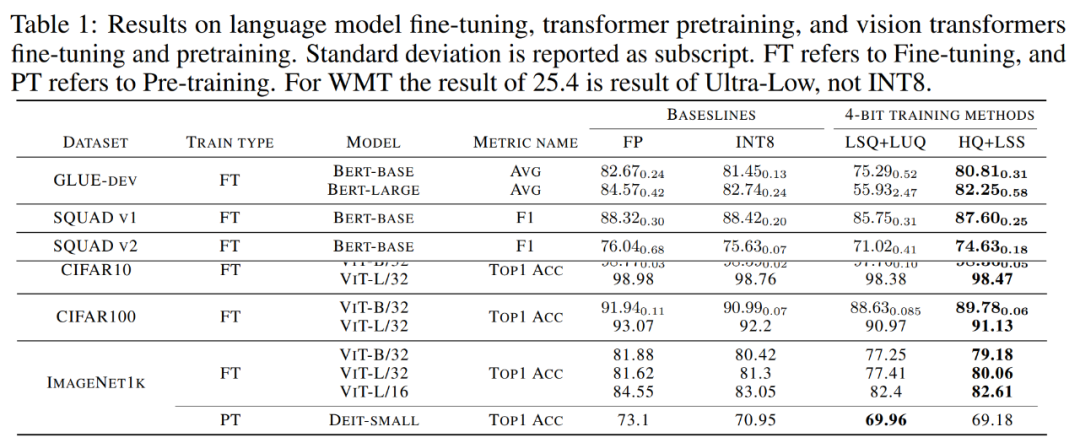 Photos
Photos
Affinement du modèle de langue. Par rapport à LSQ+LUQ, l'algorithme proposé dans l'étude améliore la précision moyenne de 5,5 % sur le modèle bert-base et de 25 % sur le modèle bert-large.
L'équipe de recherche a également démontré d'autres résultats de l'algorithme sur les ensembles de données SQUAD, SQUAD 2.0, Adversarial QA, CoNLL-2003 et SWAG. Sur toutes les tâches, cette méthode permet d'obtenir de meilleures performances par rapport à LSQ+LUQ. Par rapport à LSQ+LUQ, cette méthode permet d'obtenir des améliorations de 1,8 % et 3,6 % sur SQUAD et SQUAD 2.0, respectivement. Dans le cadre de l’AQ contradictoire plus difficile, la méthode permet d’obtenir une amélioration de 6,8 % du score F1. Sur SWAG et CoNLL-2003, cette méthode améliore la précision respectivement de 6,7 % et 4,2 %.
Traduction automatique. L'étude a également utilisé la méthode proposée pour la pré-formation. Cette méthode entraîne un modèle basé sur Transformer [51] pour la traduction automatique sur l'ensemble de données WMT 14 En-De. Le taux de dégradation du BLEU de
HQ+LSS est d'environ 1,0 %, ce qui est inférieur aux 2,1 % d'Ultra-low et supérieur aux 0,3 % rapportés dans l'article LUQ. Néanmoins, HQ+LSS fonctionne toujours de manière comparable aux méthodes existantes sur cette tâche de pré-formation et prend en charge le matériel contemporain.
Classification des images. Étudiez le chargement des points de contrôle ViT pré-entraînés sur ImageNet21k et leur réglage fin sur CIFAR-10, CIFAR-100 et ImageNet1k.
Par rapport à LSQ+LUQ, la méthode de recherche améliore la précision de ViT-B/32 et ViT-L/32 de 1,1 % et 0,2 % respectivement. Sur ImageNet1k, cette méthode améliore la précision de 2 % sur ViT-B/32, 2,6 % sur ViT-L/32 et 0,2 % sur ViT-L/32 par rapport à LSQ+LUQ.
L'équipe de recherche a ensuite testé l'efficacité de l'algorithme sur le modèle DeiT-Small pré-entraîné sur ImageNet1K, où HQ+LSS peut toujours converger vers un niveau de précision similaire à celui de LSQ+LUQ tout en étant plus convivial pour le matériel. .
Étude sur l'ablation
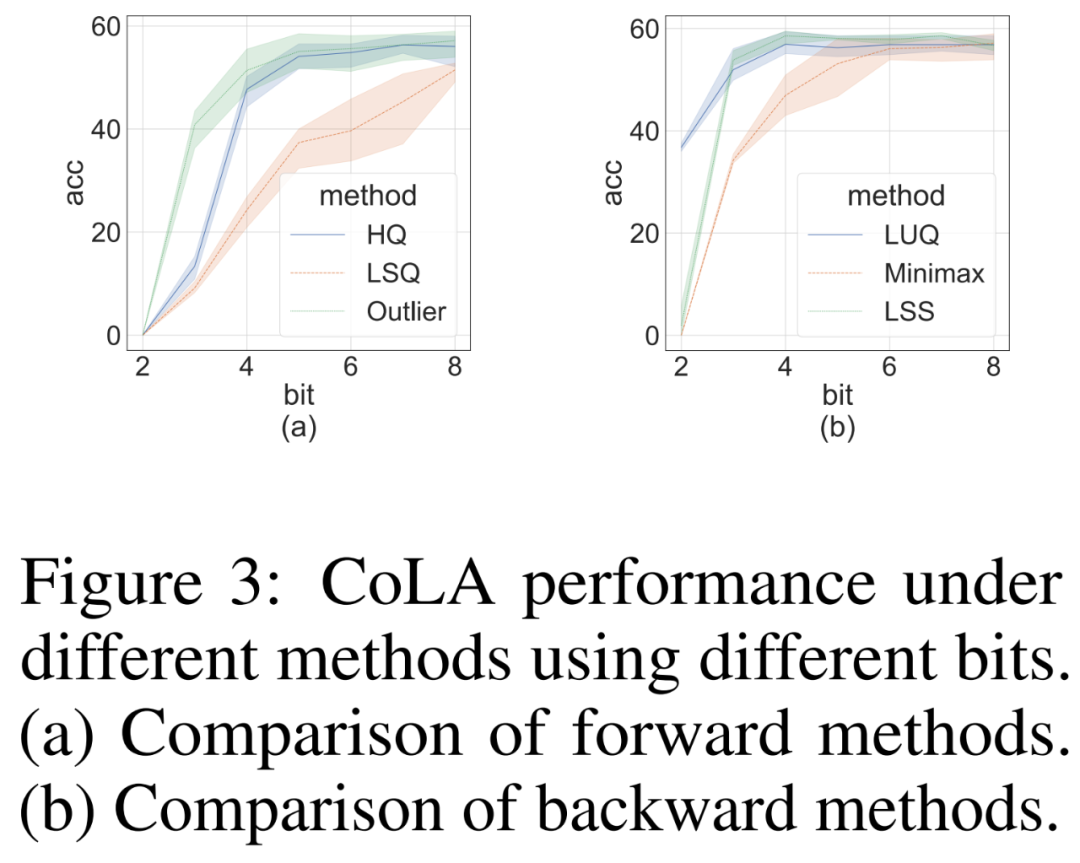
Nous avons mené des études d'ablation pour démontrer de manière indépendante l'efficacité des méthodes avant et arrière sur l'ensemble de données difficile CoLA. Pour étudier l'efficacité de différents quantificateurs sur la propagation vers l'avant, ils ont réglé la rétropropagation sur FP16. Les résultats sont présentés dans la figure 3 (a) ci-dessous.
Pour la rétropropagation, les chercheurs ont comparé un simple quantificateur minimax, LUQ, et leur propre LSS, et ont avancé la propagation vers FP16. Les résultats sont présentés dans la figure 3 (b) ci-dessous. Bien que la largeur de bits soit supérieure à 2, LSS obtient des résultats comparables, voire légèrement meilleurs, à LUQ.
 Photos
Photos
Efficacité informatique et de la mémoire
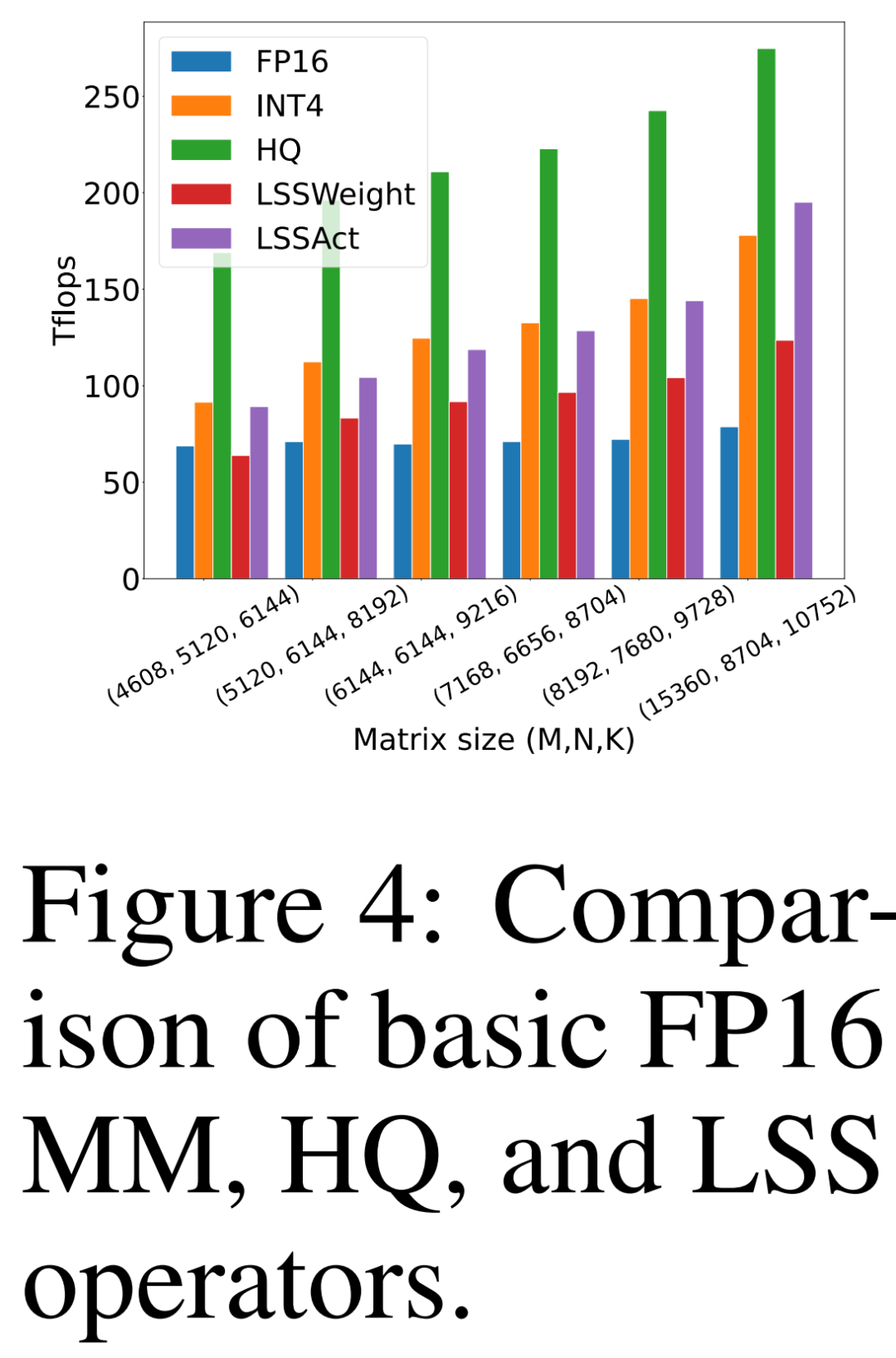
Le chercheur compare sa propre proposition HQ-MM (HQ), LSS pour calculer les gradients de poids (LSSWeight) et LSS pour calculer les gradients d'activation (LSSAct ), leur débit moyen (INT4) et l'implémentation de base Tensor Core FP16 GEMM (FP16) fournie par cutlass sur le GPU NVIDIA RTX 3090 dans la figure 4 ci-dessous, qui a un débit maximal de 142 TFLOP FP16 et 568 TFLOP INT4.
 Photos
Photos
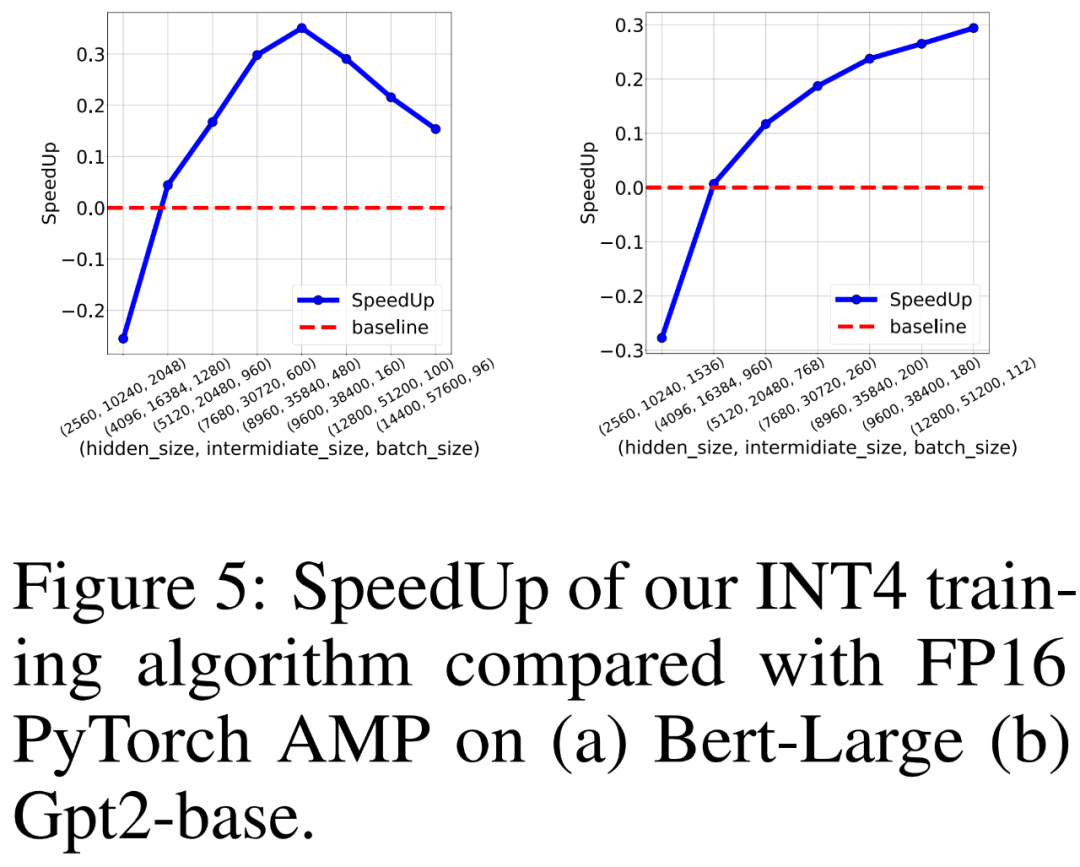
Les chercheurs ont également comparé le débit de formation du FP16 PyTorch AMP et de leur propre algorithme de formation INT4 pour la formation de modèles de langage de type BERT et GPT sur 8 GPU NVIDIA A100. Ils ont fait varier la taille de la couche cachée, la taille de la couche intermédiaire entièrement connectée et la taille du lot et ont tracé l'accélération de la formation INT4 dans la figure 5 ci-dessous.
Les résultats montrent que l'algorithme d'entraînement INT4 atteint jusqu'à 35,1 % d'accélération pour les modèles de type BERT et jusqu'à 26,5 % d'accélération pour les modèles de type GPT.
 photos
photos
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment définir les fichiers d'en-tête pour VScode
Apr 15, 2025 pm 09:09 PM
Comment définir les fichiers d'en-tête pour VScode
Apr 15, 2025 pm 09:09 PM
Comment définir des fichiers d'en-tête à l'aide du code Visual Studio? Créez un fichier d'en-tête et déclarez les symboles dans le fichier d'en-tête à l'aide du nom du suffixe .h ou .hpp (tels que les classes, les fonctions, les variables) compilez le programme à l'aide de la directive #include pour inclure le fichier d'en-tête dans le fichier source. Le fichier d'en-tête sera inclus et les symboles déclarés sont disponibles.
 Utilisez-vous C dans le code Visual Studio
Apr 15, 2025 pm 08:03 PM
Utilisez-vous C dans le code Visual Studio
Apr 15, 2025 pm 08:03 PM
L'écriture C dans VS Code est non seulement possible, mais aussi efficace et élégante. La clé consiste à installer l'excellente extension C / C, qui fournit des fonctions telles que la complétion du code, la mise en évidence de la syntaxe et le débogage. Les capacités de débogage de VS Code vous aident à localiser rapidement les bogues, tandis que la sortie PRINTF est une méthode de débogage à l'ancienne mais efficace. De plus, lorsque l'allocation de mémoire dynamique, la valeur de retour doit être vérifiée et la mémoire libérée pour éviter les fuites de mémoire, et le débogage de ces problèmes est pratique dans le code vs. Bien que VS Code ne puisse pas aider directement à l'optimisation des performances, il fournit un bon environnement de développement pour une analyse facile des performances du code. Les bonnes habitudes de programmation, la lisibilité et la maintenabilité sont également cruciales. Quoi qu'il en soit, le code vs est
 Docker utilise Yaml
Apr 15, 2025 am 07:21 AM
Docker utilise Yaml
Apr 15, 2025 am 07:21 AM
YAML est utilisé pour configurer des conteneurs, des images et des services pour Docker. Pour configurer: Pour les conteneurs, spécifiez le nom, l'image, le port et les variables d'environnement dans docker-compose.yml. Pour les images, les images de base, les commandes de construction et les commandes par défaut sont fournies dans DockerFile. Pour les services, définissez le nom, le miroir, le port, le volume et les variables d'environnement dans docker-compose.service.yml.
 Quelles technologies sous-jacentes Docker utilise-t-elle?
Apr 15, 2025 am 07:09 AM
Quelles technologies sous-jacentes Docker utilise-t-elle?
Apr 15, 2025 am 07:09 AM
Docker utilise des moteurs à conteneurs, des formats de miroir, des pilotes de stockage, des modèles de réseau, des outils d'orchestration de conteneurs, de la virtualisation du système d'exploitation et du registre des conteneurs pour prendre en charge ses capacités de conteneurisation, offrant un déploiement et une gestion d'applications légères, portables et automatisées.
 Quelle plate-forme Docker utilise pour gérer les images publiques
Apr 15, 2025 am 07:06 AM
Quelle plate-forme Docker utilise pour gérer les images publiques
Apr 15, 2025 am 07:06 AM
La plate-forme d'hébergement Docker Image est utilisée pour gérer et stocker des images Docker, ce qui permet aux développeurs et aux utilisateurs d'accéder facilement et d'utiliser des environnements logiciels préfabillés. Les plates-formes communes incluent: Docker Hub: officiellement entretenu par Docker et possède une énorme bibliothèque miroir. Registre des conteneurs GitHub: intègre l'écosystème GitHub. Google Container Registry: hébergé par Google Cloud Platform. Amazon Elastic Container Registry: Hébergé par AWS. Quay.io: par un chapeau rouge
 Lequel est le meilleur, VScode ou Visual Studio
Apr 15, 2025 pm 08:36 PM
Lequel est le meilleur, VScode ou Visual Studio
Apr 15, 2025 pm 08:36 PM
Selon les besoins spécifiques et la taille du projet, choisissez l'IDE le plus approprié: les grands projets (en particulier C #, C) et le débogage complexe: Visual Studio, qui offre des capacités de débogage puissantes et un support parfait pour les grands projets. Petits projets, prototypage rapide, machines à configuration faible: code vs, légère, vitesse de démarrage rapide, faible utilisation des ressources et évolutivité extrêmement élevée. En fin de compte, en essayant et en expérimentant VS Code et Visual Studio, vous pouvez trouver la meilleure solution pour vous. Vous pouvez même envisager d'utiliser les deux pour les meilleurs résultats.
 Docker utilise Macvlan
Apr 15, 2025 am 06:57 AM
Docker utilise Macvlan
Apr 15, 2025 am 06:57 AM
Macvlan dans Docker est un module de noyau Linux qui permet aux conteneurs d'avoir leur propre adresse MAC, permettant l'isolement du réseau, l'amélioration des performances et l'interaction directe avec le réseau physique. L'utilisation de macvlan nécessite: 1. Installez le module du noyau; 2. Créer un réseau Macvlan; 3. Affecter les segments d'adresse IP; 4. Spécifiez le réseau Macvlan lors de la création de conteneurs; 5. Vérifiez la connexion.
 Peut-il vscode exécuter kotlin
Apr 15, 2025 pm 06:57 PM
Peut-il vscode exécuter kotlin
Apr 15, 2025 pm 06:57 PM
L'exécution de Kotlin dans VS Code nécessite la configuration de l'environnement suivant: Java Development Kit (JDK) et les plugins liés au compilateur Kotlin Kotlin (tels que le langage Kotlin et l'extension Kotlin pour le code vs) créent des fichiers Kotlin et exécutez du code pour les tests pour garantir que la configuration de l'environnement est réussie





