Un moyen simple de dessiner des courbes à l'aide des astuces du didacticiel Canvas_html5 de HTML5

La méthode des courbes fournie avec Canvas2D
Récemment, j'ai étudié le calcul des corps mous 3D, j'essaie donc de rattraper quelques connaissances. Cela implique souvent des analyses numériques, principalement divers algorithmes d'interpolation de courbes. Soudain, je me suis rappelé que Canvas2D lui-même pouvait également dessiner des courbes, en utilisant des courbes de Bézier quadratiques et cubiques. En fait, je n'ai jamais utilisé cette méthode, alors essayons-la maintenant ~
Cet article ne parle que du dessin de courbes simples, et je ne parlerai pas de beaucoup de principes compliqués. De plus, le principe de la courbe de Bézier est très simple. Vous pouvez le comprendre en consultant Wikipédia. En fait, de nombreux dessins de courbes simples dans les outils de dessin utilisent des courbes de Bézier. Si vous avez utilisé les courbes des outils de dessin fournis avec Windows, vous devez les connaître. Vous pouvez d'abord tracer une ligne droite, puis cliquer à un certain endroit pour déformer la ligne droite. L'action initiale de glissement consiste à déterminer les deux sommets de la courbe, et l'action de clic consiste à ajouter un point intermédiaire. L'outil de dessin fourni avec Windows utilise une courbe de Bézier cubique et vous pouvez ajouter deux points intermédiaires. La courbe de Bézier est différente de l'interpolation polynomiale générale. Son point médian n'est utilisé que comme point de contrôle, et non comme sommet par lequel la courbe doit passer. Et il peut aussi réaliser des courbes fermées. Canvas2D propose deux méthodes pour dessiner des courbes
　quadraticCurveTo : Courbe de Bézier quadratique
　bezierCurveTo : Courbe de Bézier cubique
Les lignes sont tracées à partir de la position actuelle. Vous pouvez utiliser la méthode moveTo pour spécifier la position actuelle. Une fois que vous avez la position de départ de la courbe, vous avez également besoin du point médian et de la position finale. Transmettez simplement ces coordonnées de position à la fonction de dessin. Par exemple, une courbe de Bézier quadratique nécessite un point intermédiaire et une position finale, donc deux coordonnées doivent être transmises à la fonction quadraticCurveTo. Les coordonnées sont composées de x et y, ce qui signifie que cette fonction a 4 paramètres. bezierCurveTo est identique, sauf qu'il comporte deux points intermédiaires. Utilisons-le ci-dessous

Code CSSCopier le contenu dans le presse-papiers

1. <canvas id="toile" largeur=" 200" hauteur="200"></canvas>
2. <script>
3. var g=canvas.getContext("2d"
);
4. //Ligne droite ordinaire
5. g.beginPath();
6. g.StrokeStyle="#CCC"
7. g.moveTo(0,0);
8. g.lineTo(200,0);
9. g.lineTo(0,200);
10. g.lineTo(200 200);
11. g.AVC();
12. //Courbe de Bez
13. g.beginPath();
14. g.StrokeStyle="#F00"
15. g.moveTo(0,0);
16. g.bezierCurveTo(200,0, 0,200, 200,200)
17. g.AVC();
18. </script>

Cela donne quatre points selon la trajectoire en forme de Z et dessine des lignes droites ordinaires et des courbes de Bézier. C'est juste une courbe ordinaire. L'avantage de la courbe de Bézier est qu'elle peut dessiner des courbes fermées, comme ce morceau de code

.

Code CSSCopier le contenu dans le presse-papiers

1. g.beginPath();
2. g.StrokeStyle="#00F"
3. g.moveTo(100,0);
4. g.bezierCurveTo(-100 200, 300 200, 100,0);
5. g.AVC();

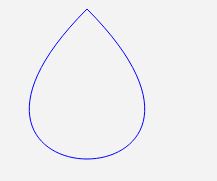
Définissez les positions de début et de fin de la courbe de Bézier cubique au même point pour dessiner une courbe fermée. Étant donné que la direction d'interpolation de la courbe de Bézier ne suit pas l'axe des coordonnées, une courbe fermée peut être dessinée. Si nous voulons que l'interpolation polynomiale dessine une courbe fermée, nous devons convertir les paramètres et utiliser le système de coordonnées polaires pour compléter.
Les exemples que j'utilise sont tous des courbes de Bézier cubiques. En fait, la deuxième étape est la même, mais sans le point médian, je ne peux pas dessiner ce que je veux. Je ne vais pas trop m’étendre, c’est tout pour cet article ==. .