 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Le nouveau papier brûlant de Microsoft : Transformer s'étend à 1 milliard de jetons
Le nouveau papier brûlant de Microsoft : Transformer s'étend à 1 milliard de jetons
Le nouveau papier brûlant de Microsoft : Transformer s'étend à 1 milliard de jetons
Alors que chacun continue de mettre à niveau et d'itérer ses propres grands modèles, la capacité du LLM (Large Language Model) à traiter les fenêtres contextuelles est également devenue un indicateur d'évaluation important.
Par exemple, le grand modèle de célébrité GPT-4 prend en charge 32 000 jetons, ce qui équivaut à 50 pages de texte ; Anthropic, fondée par un ancien membre d'OpenAI, a augmenté les capacités de traitement des jetons de Claude à 100 000, soit environ 75 000 mots, ce qui équivaut à peu près à un résumé en un clic de la première partie de "Harry Potter".
Dans les dernières recherches de Microsoft, ils ont cette fois directement étendu Transformer à 1 milliard de jetons. Cela ouvre de nouvelles possibilités pour modéliser des séquences très longues, comme par exemple traiter un corpus entier ou même l'ensemble d'Internet comme une seule séquence.
À titre de comparaison, une personne moyenne peut lire 100 000 jetons en 5 heures environ et peut prendre plus de temps pour digérer, mémoriser et analyser ces informations. Claude peut le faire en moins d'une minute. S’il était converti en cette recherche par Microsoft, ce serait un nombre stupéfiant.
 Photos
Photos
- Adresse papier : https://arxiv.org/pdf/2307.02486.pdf
- Adresse du projet : https://github.com/microsoft/unilm/tree/master
Plus précisément, la recherche propose LONGNET, une variante de Transformer qui peut étendre la longueur des séquences à plus d'un milliard de jetons sans sacrifier les performances sur des séquences plus courtes. L'article propose également une attention dilatée, qui peut élargir de manière exponentielle la plage de perception du modèle.
LONGNET présente les avantages suivants :
1) Il a une complexité de calcul linéaire
2) Il peut être utilisé comme entraîneur distribué pour des séquences plus longues
3) l'attention dilatée peut être ; utilisé sans Seam remplace l'attention standard et peut être intégré de manière transparente aux méthodes d'optimisation existantes basées sur Transformer.
Les résultats expérimentaux montrent que LONGNET présente de solides performances à la fois dans la modélisation de séquences longues et dans les tâches de langage général.
En termes de motivation de la recherche, l'article indique qu'au cours des dernières années, l'extension des réseaux de neurones est devenue une tendance et que de nombreux réseaux performants ont été étudiés. Parmi eux, la longueur de la séquence, en tant que partie du réseau neuronal, devrait idéalement être infinie. Mais la réalité est souvent inverse, donc dépasser la limite de longueur de séquence apportera des avantages significatifs :
- Premièrement, cela fournit au modèle une mémoire et un champ récepteur de grande capacité, lui permettant de communiquer efficacement avec les humains et les monde.
- Deuxièmement, un contexte plus long contient des relations causales et des chemins de raisonnement plus complexes que le modèle peut exploiter dans les données d'entraînement. Au contraire, des dépendances plus courtes introduiront des corrélations plus parasites, ce qui ne favorise pas la généralisation du modèle.
- Troisièmement, une séquence plus longue peut aider le modèle à explorer des contextes plus longs, et des contextes extrêmement longs peuvent également aider le modèle à atténuer le problème catastrophique de l'oubli.
Cependant, le principal défi dans l'extension de la longueur des séquences est de trouver le bon équilibre entre la complexité informatique et la puissance d'expression du modèle.
Par exemple, les modèles de style RNN sont principalement utilisés pour augmenter la longueur des séquences. Cependant, sa nature séquentielle limite la parallélisation lors de l’entraînement, ce qui est crucial dans la modélisation de séquences longues.
Récemment, les modèles spatiaux d'états sont devenus très attrayants pour la modélisation de séquences, qui peuvent être exécutés comme un CNN pendant la formation et convertis en un RNN efficace au moment du test. Cependant, ce type de modèle ne fonctionne pas aussi bien que Transformer aux longueurs régulières.
Une autre façon d'étendre la longueur de la séquence est de réduire la complexité du Transformateur, c'est-à-dire la complexité quadratique de l'attention personnelle. À ce stade, certaines variantes efficaces basées sur Transformer ont été proposées, notamment l'attention de bas rang, les méthodes basées sur le noyau, les méthodes de sous-échantillonnage et les méthodes basées sur la récupération. Cependant, ces approches n'ont pas encore étendu Transformer à l'échelle d'un milliard de jetons (voir Figure 1).
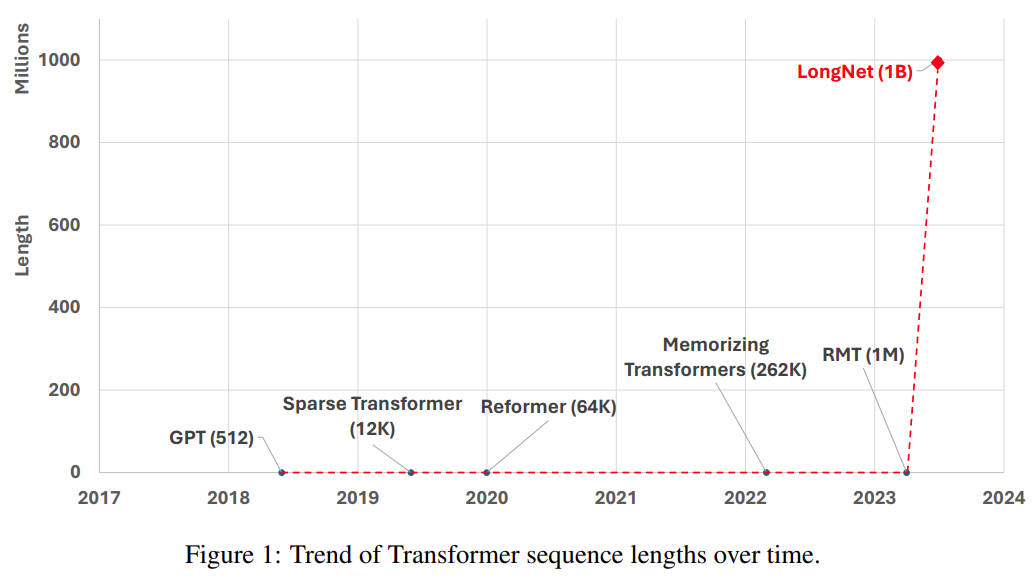 Photos
Photos
Le tableau suivant montre la comparaison de la complexité informatique de différentes méthodes de calcul. N est la longueur de la séquence et d est la dimension cachée.
 photos
photos
Méthode
La solution de recherche LONGNET a réussi à étendre la longueur de la séquence à 1 milliard de jetons. Plus précisément, cette recherche propose un nouveau composant appelé attention dilatée et remplace le mécanisme d'attention de Vanilla Transformer par une attention dilatée. Un principe général de conception est que l’allocation de l’attention diminue de façon exponentielle à mesure que la distance entre les jetons augmente. L'étude montre que cette approche de conception obtient une complexité de calcul linéaire et une dépendance logarithmique entre les jetons. Cela résout le conflit entre les ressources d’attention limitées et l’accès à chaque jeton.
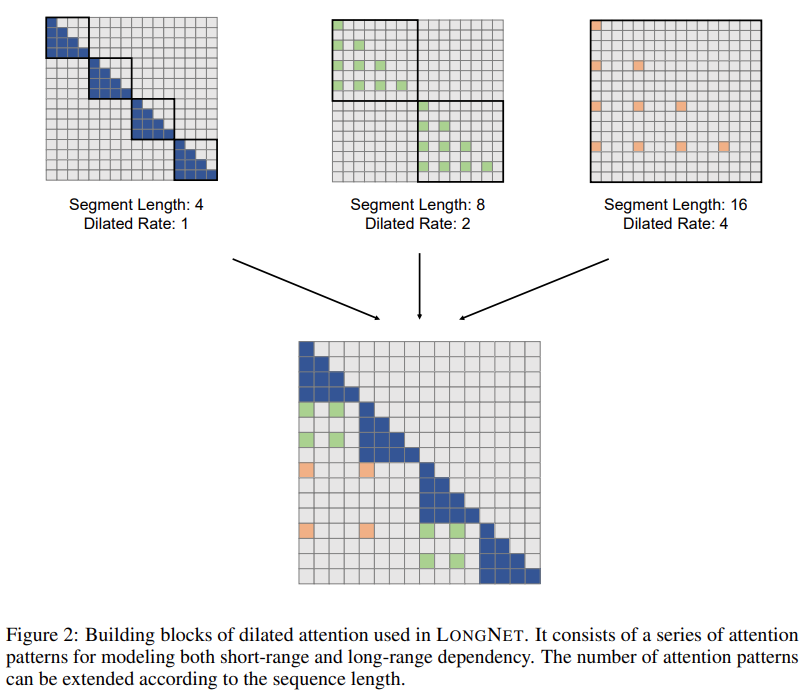 Pictures
Pictures
Pendant la mise en œuvre, LONGNET peut être converti en un transformateur dense pour prendre en charge de manière transparente les méthodes d'optimisation existantes pour les transformateurs (telles que la fusion du noyau, la quantification et la formation distribuée). Tirant parti de la complexité linéaire, LONGNET peut être entraîné en parallèle sur plusieurs nœuds, en utilisant des algorithmes distribués pour briser les contraintes de calcul et de mémoire.
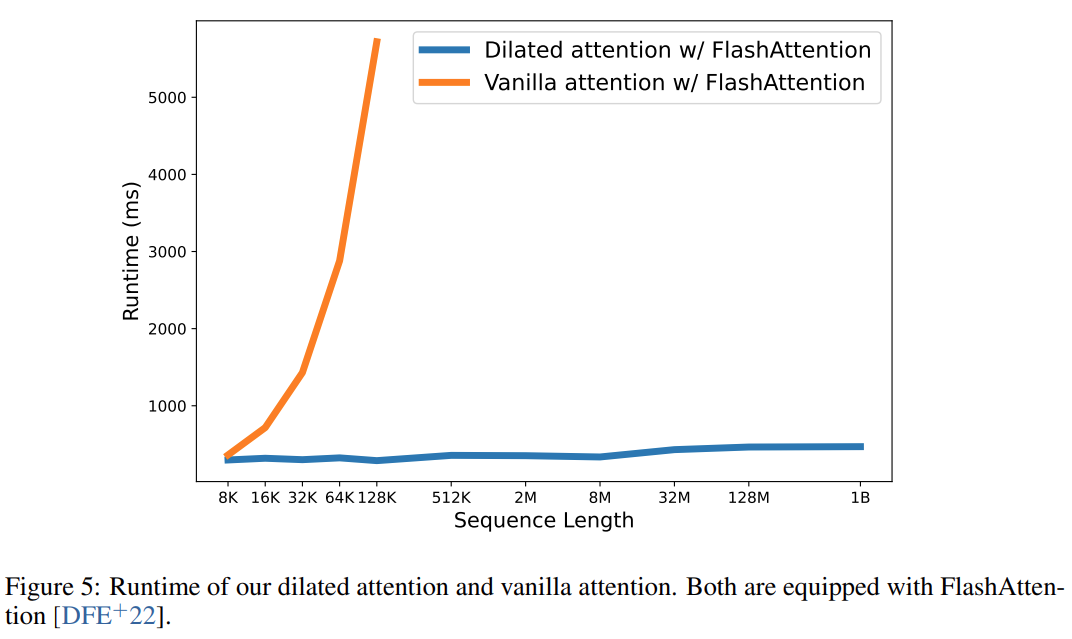
En fin de compte, cette recherche a effectivement étendu la longueur de la séquence à 1 milliard de jetons, et la durée d'exécution était presque constante, comme le montre la figure ci-dessous. En revanche, le temps d'exécution du Transformer Vanilla souffre d'une complexité quadratique.
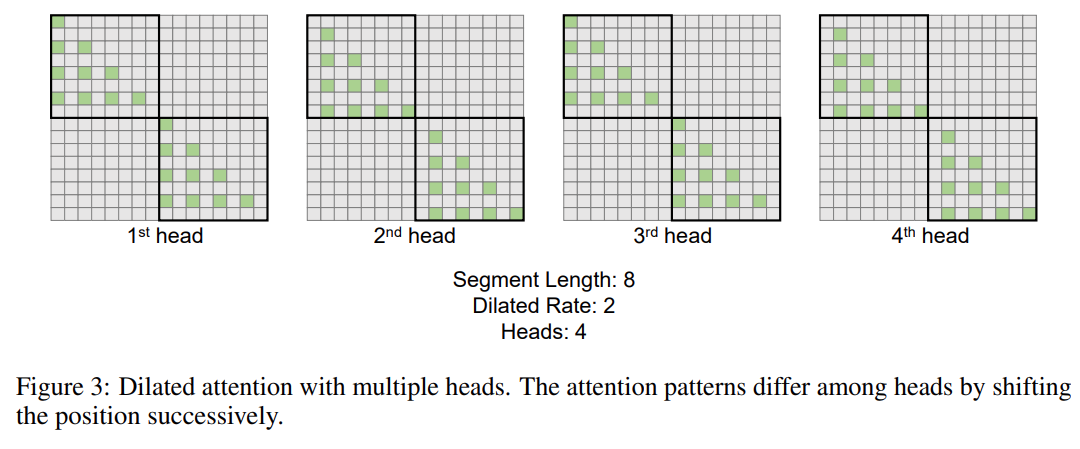
Cette recherche introduit en outre le mécanisme d'attention dilatée à plusieurs têtes. Comme le montre la figure 3 ci-dessous, cette étude effectue différents calculs sur différentes têtes en fragmentant différentes parties des paires requête-clé-valeur.
 Photos
Photos
Formation distribuée
Bien que la complexité informatique de l'attention dilatée ait été considérablement réduite à 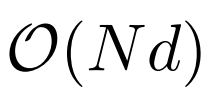 , en raison des limitations de l'informatique et de la mémoire, elle adaptera la longueur de la séquence à des millions n’est pas réalisable. Il existe certains algorithmes de formation distribués pour la formation de modèles à grande échelle, tels que le parallélisme de modèles [SPP+19], le parallélisme de séquences [LXLY21, KCL+22] et le parallélisme de pipeline [HCB+19]. , surtout lorsque la dimension de la séquence est très grande.
, en raison des limitations de l'informatique et de la mémoire, elle adaptera la longueur de la séquence à des millions n’est pas réalisable. Il existe certains algorithmes de formation distribués pour la formation de modèles à grande échelle, tels que le parallélisme de modèles [SPP+19], le parallélisme de séquences [LXLY21, KCL+22] et le parallélisme de pipeline [HCB+19]. , surtout lorsque la dimension de la séquence est très grande.
Cette recherche utilise la complexité informatique linéaire de LONGNET pour la formation distribuée des dimensions de séquence. La figure 4 ci-dessous montre l'algorithme distribué sur deux GPU, qui peut être étendu à n'importe quel nombre d'appareils.
Expériences
L'étude a comparé LONGNET avec Vanilla Transformer et Sparse Transformer. La différence entre les architectures réside dans la couche d’attention, tandis que les autres couches restent les mêmes. Les chercheurs ont étendu la longueur de séquence de ces modèles de 2K à 32K, tout en réduisant la taille des lots pour garantir que le nombre de jetons dans chaque lot reste inchangé.
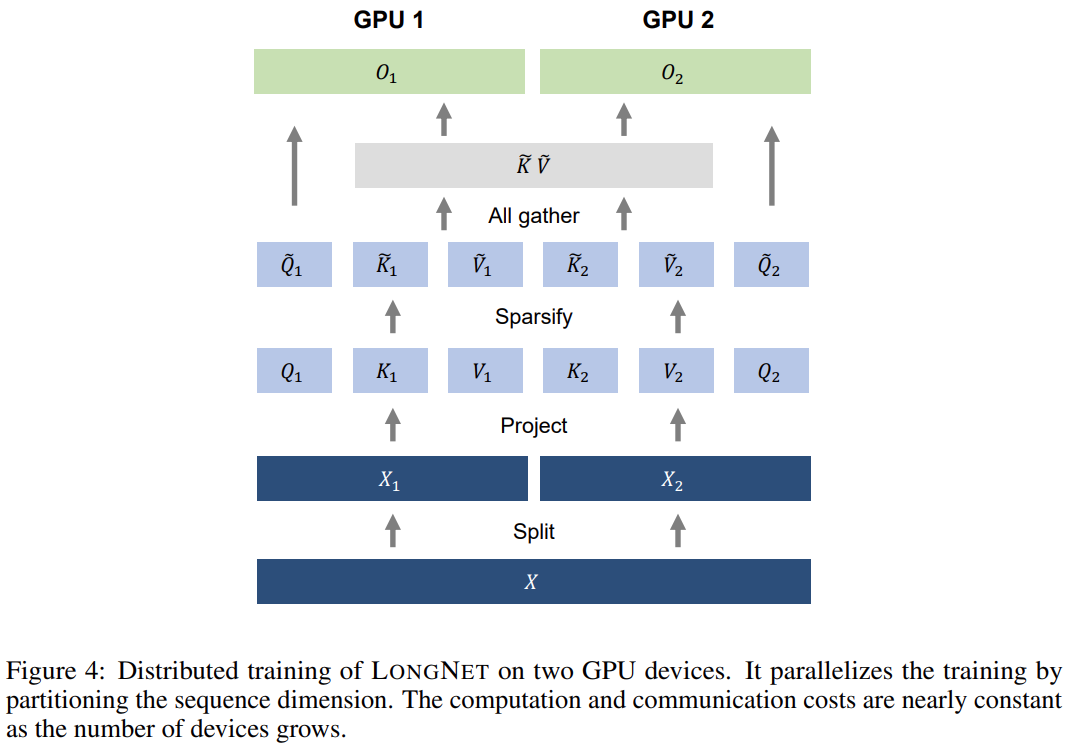
Le Tableau 2 résume les résultats de ces modèles sur l'ensemble de données Stack. La recherche utilise la complexité comme mesure d’évaluation. Les modèles ont été testés en utilisant différentes longueurs de séquence, allant de 2k à 32k. Lorsque la longueur d'entrée dépasse la longueur maximale prise en charge par le modèle, la recherche met en œuvre une attention causale par blocs (BCA) [SDP+22], une méthode d'extrapolation de pointe pour l'inférence de modèle de langage.
De plus, l'étude a supprimé le codage de position absolue. Premièrement, les résultats montrent que l’augmentation de la longueur des séquences au cours de la formation aboutit généralement à de meilleurs modèles de langage. Deuxièmement, la méthode d’extrapolation de la longueur de séquence dans l’inférence ne s’applique pas lorsque la longueur est beaucoup plus grande que celle prise en charge par le modèle. Enfin, LONGNET surpasse systématiquement les modèles de base, démontrant son efficacité dans la modélisation du langage.
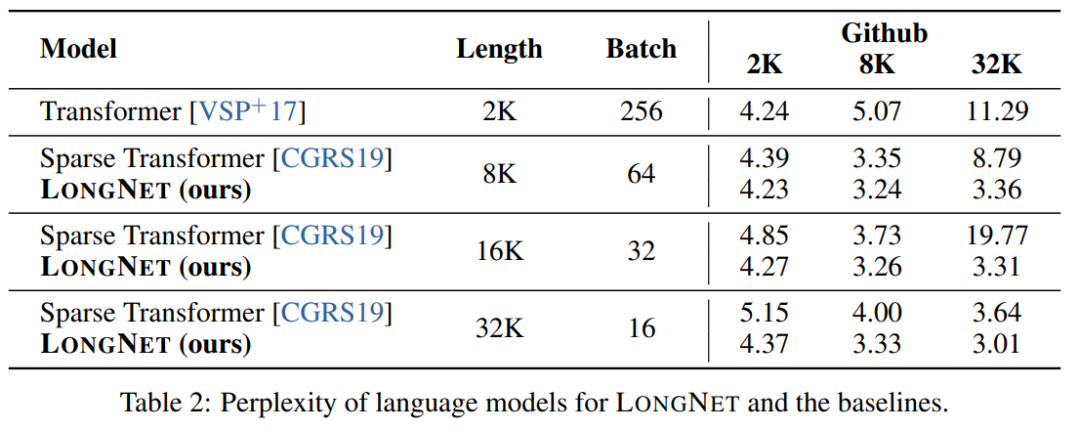
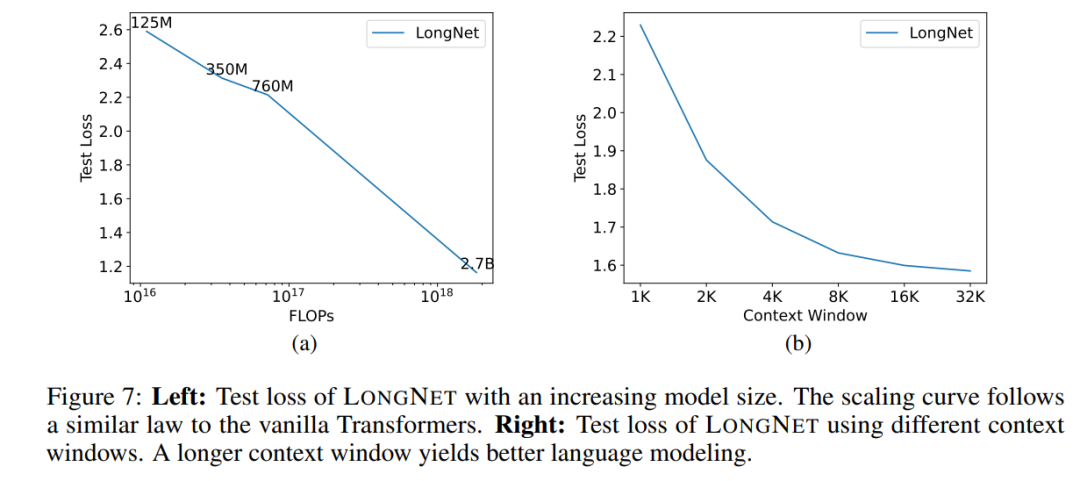
Courbe d'expansion de la longueur de la séquence
La figure 6 trace les courbes d'expansion de la longueur de séquence du transformateur vanille et de LONGNET. Cette étude estime l'effort de calcul en comptant le total des échecs des multiplications matricielles. Les résultats montrent que Vanilla Transformer et LONGNET atteignent des longueurs de contexte plus grandes grâce à la formation. Cependant, LONGNET peut étendre la longueur du contexte plus efficacement, réduisant ainsi les pertes de test avec moins de calculs. Cela démontre l’avantage d’intrants de formation plus longs par rapport à l’extrapolation. Les expériences montrent que LONGNET est un moyen plus efficace d'étendre la longueur du contexte dans les modèles de langage. En effet, LONGNET peut apprendre plus efficacement des dépendances plus longues. Une propriété importante des grands modèles de langage est que la perte augmente dans une loi de puissance à mesure que la quantité de calcul augmente. Pour vérifier si LONGNET suit toujours des règles de mise à l'échelle similaires, l'étude a formé une série de modèles avec différentes tailles (de 125 millions à 2,7 milliards de paramètres). 2,7 milliards de modèles ont été formés avec 300 milliards de jetons, tandis que les modèles restants ont utilisé environ 400 milliards de jetons. La figure 7 (a) représente la courbe d'échelle de LONGNET par rapport au calcul. L'étude a calculé la complexité sur le même ensemble de tests. Cela prouve que LONGNET peut toujours suivre une loi de puissance. Cela signifie également que Transformer dense n'est pas une condition préalable à l'extension des modèles de langage. De plus, l'évolutivité et l'efficacité sont gagnées avec LONGNET.
Invite contextuelle longue
L'invite est un moyen important de guider le modèle de langage et de lui fournir des informations supplémentaires. Cette étude valide expérimentalement si LONGNET peut bénéficier de fenêtres d'indication de contexte plus longues.Cette étude a retenu un préfixe (préfixes) comme invite et a testé la perplexité de ses suffixes (suffixes). De plus, au cours du processus de recherche, l’invite a été progressivement étendue de 2K à 32K. Pour faire une comparaison équitable, la longueur du suffixe est maintenue constante tandis que la longueur du préfixe est augmentée jusqu'à la longueur maximale du modèle. La figure 7 (b) rapporte les résultats sur l'ensemble de test. Cela montre que la perte de test de LONGNET diminue progressivement à mesure que la fenêtre de contexte augmente. Cela prouve la supériorité de LONGNET dans l'utilisation complète du contexte long pour améliorer les modèles de langage.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
![Comment afficher la vitesse Internet sur la barre des tâches [étapes faciles]](https://img.php.cn/upload/article/000/465/014/169088173253603.png?x-oss-process=image/resize,m_fill,h_207,w_330) Comment afficher la vitesse Internet sur la barre des tâches [étapes faciles]
Aug 01, 2023 pm 05:22 PM
Comment afficher la vitesse Internet sur la barre des tâches [étapes faciles]
Aug 01, 2023 pm 05:22 PM
La vitesse d'Internet est un paramètre important pour déterminer le résultat de votre expérience en ligne. Qu'il s'agisse de télécharger ou de télécharger des fichiers ou simplement de naviguer sur le Web, nous avons tous besoin d'une connexion Internet décente. C'est pourquoi les utilisateurs recherchent des moyens d'afficher la vitesse d'Internet sur la barre des tâches. L'affichage de la vitesse du réseau dans la barre des tâches permet aux utilisateurs de surveiller les choses rapidement, quelle que soit la tâche à accomplir. La barre des tâches est toujours visible sauf si vous êtes en mode plein écran. Mais Windows ne propose pas d'option native pour afficher la vitesse Internet dans la barre des tâches. C'est pourquoi vous avez besoin d'outils tiers. Lisez la suite pour tout savoir sur les meilleures options ! Comment exécuter un test de vitesse depuis la ligne de commande Windows ? Appuyez sur + pour ouvrir Exécuter, tapez Power Shell et appuyez sur ++. Fenêtre
 Correctif : problème de connexion réseau qui empêche l'accès à Internet en mode sans échec de Windows 11
Sep 23, 2023 pm 01:13 PM
Correctif : problème de connexion réseau qui empêche l'accès à Internet en mode sans échec de Windows 11
Sep 23, 2023 pm 01:13 PM
Ne pas avoir de connexion Internet sur votre ordinateur Windows 11 en mode sans échec avec réseau peut être frustrant, en particulier lors du diagnostic et du dépannage des problèmes du système. Dans ce guide, nous discuterons des causes potentielles du problème et énumérerons des solutions efficaces pour garantir que vous puissiez accéder à Internet en mode sans échec. Pourquoi n’y a-t-il pas Internet en mode sans échec avec réseau ? La carte réseau est incompatible ou ne se charge pas correctement. Des pare-feu, des logiciels de sécurité ou des logiciels antivirus tiers peuvent interférer avec les connexions réseau en mode sans échec. Le service réseau ne fonctionne pas. Infection par logiciel malveillant Que dois-je faire si Internet ne peut pas être utilisé en mode sans échec sous Windows 11 ? Avant d'effectuer des étapes de dépannage avancées, vous devez envisager d'effectuer les vérifications suivantes : Assurez-vous d'utiliser
 Le papier Stable Diffusion 3 est enfin publié, et les détails architecturaux sont révélés. Cela aidera-t-il à reproduire Sora ?
Mar 06, 2024 pm 05:34 PM
Le papier Stable Diffusion 3 est enfin publié, et les détails architecturaux sont révélés. Cela aidera-t-il à reproduire Sora ?
Mar 06, 2024 pm 05:34 PM
L'article de StableDiffusion3 est enfin là ! Ce modèle est sorti il y a deux semaines et utilise la même architecture DiT (DiffusionTransformer) que Sora. Il a fait beaucoup de bruit dès sa sortie. Par rapport à la version précédente, la qualité des images générées par StableDiffusion3 a été considérablement améliorée. Il prend désormais en charge les invites multithèmes, et l'effet d'écriture de texte a également été amélioré et les caractères tronqués n'apparaissent plus. StabilityAI a souligné que StableDiffusion3 est une série de modèles avec des tailles de paramètres allant de 800M à 8B. Cette plage de paramètres signifie que le modèle peut être exécuté directement sur de nombreux appareils portables, réduisant ainsi considérablement l'utilisation de l'IA.
 Prix papier ICCV'23 'Combat des Dieux' ! Meta Divide Everything et ControlNet ont été sélectionnés conjointement, et un autre article a surpris les juges.
Oct 04, 2023 pm 08:37 PM
Prix papier ICCV'23 'Combat des Dieux' ! Meta Divide Everything et ControlNet ont été sélectionnés conjointement, et un autre article a surpris les juges.
Oct 04, 2023 pm 08:37 PM
ICCV2023, la plus grande conférence sur la vision par ordinateur qui s'est tenue à Paris, en France, vient de se terminer ! Le prix du meilleur article de cette année est simplement un « combat entre dieux ». Par exemple, les deux articles qui ont remporté le prix du meilleur article incluaient ControlNet, un travail qui a bouleversé le domaine de l'IA graphique vincentienne. Depuis qu'il est open source, ControlNet a reçu 24 000 étoiles sur GitHub. Qu'il s'agisse des modèles de diffusion ou de l'ensemble du domaine de la vision par ordinateur, le prix de cet article est bien mérité. La mention honorable du prix du meilleur article a été décernée à un autre article tout aussi célèbre, le modèle SAM « Séparez tout » de Meta. Depuis son lancement, « Segment Everything » est devenu la « référence » pour divers modèles d'IA de segmentation d'images, y compris ceux venus de derrière.
 NeRF et le passé et le présent de la conduite autonome, résumé de près de 10 articles !
Nov 14, 2023 pm 03:09 PM
NeRF et le passé et le présent de la conduite autonome, résumé de près de 10 articles !
Nov 14, 2023 pm 03:09 PM
Depuis que Neural Radiance Fields a été proposé en 2020, le nombre d'articles connexes a augmenté de façon exponentielle. Il est non seulement devenu une branche importante de la reconstruction tridimensionnelle, mais est également progressivement devenu actif à la frontière de la recherche en tant qu'outil important pour la conduite autonome. . NeRF a soudainement émergé au cours des deux dernières années, principalement parce qu'il ignore l'extraction et la mise en correspondance des points caractéristiques, la géométrie et la triangulation épipolaires, le PnP plus l'ajustement du faisceau et d'autres étapes du pipeline de reconstruction CV traditionnel, et ignore même la reconstruction du maillage, la cartographie et le traçage de la lumière. , directement à partir de la 2D L'image d'entrée est utilisée pour apprendre un champ de rayonnement, puis une image rendue qui se rapproche d'une photo réelle est sortie du champ de rayonnement. En d’autres termes, supposons qu’un modèle tridimensionnel implicite basé sur un réseau neuronal s’adapte à la perspective spécifiée.
 Les illustrations papier peuvent également être générées automatiquement, en utilisant le modèle de diffusion, et sont également acceptées par l'ICLR.
Jun 27, 2023 pm 05:46 PM
Les illustrations papier peuvent également être générées automatiquement, en utilisant le modèle de diffusion, et sont également acceptées par l'ICLR.
Jun 27, 2023 pm 05:46 PM
L'IA générative a pris d'assaut la communauté de l'intelligence artificielle. Les particuliers et les entreprises ont commencé à s'intéresser à la création d'applications de conversion modale associées, telles que les images Vincent, les vidéos Vincent, la musique Vincent, etc. Récemment, plusieurs chercheurs d'institutions de recherche scientifique telles que ServiceNow Research et LIVIA ont tenté de générer des graphiques dans des articles basés sur des descriptions textuelles. À cette fin, ils ont proposé une nouvelle méthode de FigGen, et l’article correspondant a également été inclus dans ICLR2023 sous le nom de TinyPaper. Adresse du document illustré : https://arxiv.org/pdf/2306.00800.pdf Certaines personnes peuvent se demander : pourquoi est-il si difficile de générer les graphiques dans le document ? En quoi cela aide-t-il la recherche scientifique ?
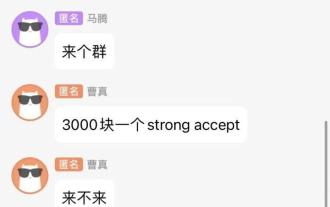 Les captures d'écran du chat révèlent les règles cachées de l'examen de l'IA ! AAAI 3000 yuans, c'est fort accepté ?
Apr 12, 2023 am 08:34 AM
Les captures d'écran du chat révèlent les règles cachées de l'examen de l'IA ! AAAI 3000 yuans, c'est fort accepté ?
Apr 12, 2023 am 08:34 AM
Alors que la date limite de soumission des articles pour l'AAAI 2023 approchait, une capture d'écran d'une discussion anonyme dans le groupe de soumission d'IA est soudainement apparue sur Zhihu. L'un d'eux a affirmé qu'il pouvait fournir un service « 3 000 yuans par acceptation forte ». Dès que la nouvelle est sortie, elle a immédiatement suscité l’indignation du public parmi les internautes. Cependant, ne vous précipitez pas encore. Le patron de Zhihu, "Fine Tuning", a déclaré qu'il s'agissait probablement simplement d'un "plaisir verbal". Selon "Fine Tuning", les salutations et les délits de gangs sont des problèmes inévitables dans tous les domaines. Avec l'essor de l'openreview, les différents inconvénients du cmt sont devenus de plus en plus évidents. L'espace laissé aux petits cercles pour fonctionner deviendra plus petit à l'avenir, mais il y aura toujours de la place. Parce qu'il s'agit d'un problème personnel, pas d'un problème avec le système et le mécanisme de soumission. Présentation de l'open r
 Classement CVPR 2023 publié, le taux d'acceptation est de 25,78% ! 2 360 articles ont été acceptés et le nombre de soumissions a grimpé à 9 155
Apr 13, 2023 am 09:37 AM
Classement CVPR 2023 publié, le taux d'acceptation est de 25,78% ! 2 360 articles ont été acceptés et le nombre de soumissions a grimpé à 9 155
Apr 13, 2023 am 09:37 AM
Tout à l'heure, le CVPR 2023 a publié un article disant : Cette année, nous avons reçu un nombre record de 9 155 articles (12 % de plus que le CVPR2022) et accepté 2 360 articles, avec un taux d'acceptation de 25,78 %. Selon les statistiques, le nombre de soumissions au CVPR n'a augmenté que de 1 724 à 2 145 au cours des 7 années allant de 2010 à 2016. Après 2017, il a grimpé en flèche et est entré dans une période de croissance rapide. En 2019, il a dépassé les 5 000 pour la première fois, et en 2022, le nombre de candidatures avait atteint 8 161. Comme vous pouvez le constater, un total de 9 155 articles ont été soumis cette année, ce qui constitue un record. Une fois l’épidémie atténuée, le sommet CVPR de cette année se tiendra au Canada. Cette année, il s'agira d'une conférence à voie unique et la traditionnelle sélection orale sera annulée. recherche Google





