J'ai secrètement regardé quelques bases informatiques, et désormais apprendre Java, c'est comme tricher !

Avant d'apprendre Java, j'aimerais poser une question Pensez-vous qu'il est nécessaire d'apprendre les bases de l'informatique ?

Beaucoup de gens pensent qu'il n'est pas nécessaire de lire ces connaissances de base ennuyeuses et obscures. Il est préférable de commencer directement depuis HelloWorld. Touchez d'abord le programme, faites-vous une impression, et le code s'exécutera, puis apprenez progressivement la syntaxe de. le programme en profondeur, et enfin utiliser le programme pour construire le projet. C'est la méthode d'apprentissage pratique.

Tout d'abord, je ne nie pas cette manière d'apprendre. Elle est en effet plus adaptée à certains étudiants, notamment ceux qui ont hâte de trouver un emploi. Apprenez d'abord à l'utiliser. Quant au principe, vous pouvez lentement. comprendre en profondeur plus tard. Après tout, rien n'est plus important que le pain ?

Mais pour nos étudiants qui apprennent les logarithmes à partir de zéro, je recommande quand même de commencer par quelques connaissances de base en informatique pour comprendre les idées et le bon sens de la programmation, ce qui sera également très utile pour notre future étude. C'est comme construire une maison. Certaines personnes construisent des maisons au toit de chaume, d'autres construisent des maisons en terre cuite et d'autres veulent construire une maison à deux étages de style occidental. La profondeur des fondations détermine directement le niveau des réalisations futures.

Alors maintenant, comprenons brièvement quelques connaissances de base en informatique.

1. Classification du langage machine

Langage machine

Le langage machine est un langage qui peut être directement reconnu par les ordinateurs. C'est un langage informatique directement exprimé en instructions de code binaire. C'est un code composé d'une chaîne de 0 et de 1, avec un certain nombre de chiffres, et divisé en plusieurs segments. Le codage de chaque segment représente une signification différente. Par exemple, ce qui suit est une simple chaîne de codes machine :

010100100000  // 520

Tant de gens se demandent pourquoi le code machine est-il composé de 0 et 1 ?

Étant donné que le code machine doit contrôler le matériel informatique pour répondre aux instructions du programme, 0 représente un potentiel faible, 1 représente un potentiel élevé, de sorte qu'un circuit logique puisse être généré, ce qui équivaut à contrôler un interrupteur, 0 est fermé et. 1 est ouvert.

Langage assembleur

Le langage assembleur est un langage destiné aux développeurs. Étant donné que le langage machine est composé uniquement de 0 et de 1, il est difficile pour les développeurs de le contrôler et de l'utiliser directement, c'est pourquoi certains symboles spéciaux doivent être utilisés comme marqueurs pour les codes binaires. Les développeurs complètent l'émission des instructions en saisissant ces symboles spéciaux et laissent l'ordinateur travailler pour nous. Les ordinateurs ne peuvent pas reconnaître directement le langage assembleur et un logiciel est nécessaire pour traduire le langage assembleur en langage machine. La différence entre celui-ci et le langage machine réside dans la méthode de représentation des instructions. Le corps principal du langage assembleur est constitué par les instructions d'assemblage. Par rapport aux instructions machine, il est plus facile pour les programmeurs de s'en souvenir.

MOV AX,1234H  //汇编指令: 寄存器AX的内容送到1234H中
101110000011010000010010 //机器指令

Langages de haut niveau

Les langages de haut niveau courants sont : c, c++, java, python, php, etc.

Il est plus proche de notre pensée humaine normale. Sa plus grande caractéristique est qu'il est facile à écrire et que le code est lisible. Pour obtenir la même fonction, il faut moins de temps pour utiliser des langages de haut niveau, le code du programme est plus court et plus facile à lire. Deuxièmement, les langages de haut niveau sont portables, c'est-à-dire qu'un morceau de code peut être exécuté sur différents types d'ordinateurs avec peu ou pas de modifications.

print('Hello World')   // python版HelloWorld

我们从这个程序可以看出来，高级语言屏蔽了机器内部指令运行细节，我们可以像写作一样书写程序，而不用关心语言内部的实现细节，这大大提高了我们的开发效率，节约开发成本。

当然，其缺点也很明显，使用高级语言编写的程序运行时，需要先将其翻译成低级语言计算机才能运行它，在翻译过程中可能会产生一些多余的部分，运行效率低些。另外，对硬件的可控性相对于低级语言弱些，目标代码量较大。

二. 进制

推荐使用在线工具进行进制转换：

https://tool.oschina.net/hexconvert/

二进制

由数字0和1组成，逢二进一，比如机器码就是二进制的，是最简单的计算机可读懂的代码，例如 0101（表示十进制数字5）。

八进制

由1到7组成的数字串，数字最大不会超过7，逢八进一，例如 157(表示十进制数字111)

十进制

我们日常使用的数字都是十进制类型的，逢十进一，例如 0123456789。

十六进制

由1到9，a-f（或者是A-F，分别代表10-15）组成的数字串，数字最大不会超过15，其中字母是不区分大小写的，逢十六进一，例如0F83（表示十进制数3971）

进制转换

1. K进制与十进制数的转换

假设有一个n+1位的K进制数，它的形式如下：

AnAn-1…A3A2A1A0
则它的大小为：（也就是对应的我们能看懂的十进制数为）

A0 * K^0 + A1 * K^1....+ An * K^n      //K^n表示K的n次方

二进制数：10101 转换成 十进制数为：21

 1*2^4 + 0*2^3 + 1*2^2 + 0*2^1+1*2^0 = 21

2. 十进制与k进制的转换

短除法。

举个栗子：

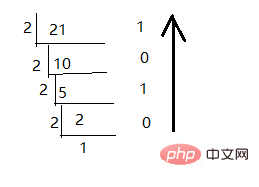
从图可以看出，用十进制数21一直除以2，每次得到的余数倒数就是最后的二进制数10101。同样，十进制转八进制、十进制转十六进制都是一样的套路，非常简单。

3. 二进制与八进制和十六进制之间转换

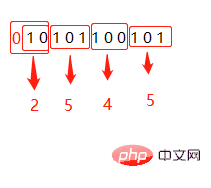
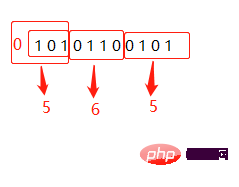
8是2的3次方，16是2的4次方，所以这之间的转换存在一种快捷方法。以2转8示例，将2进制从低位到高位，每3个一组，如果是十六进制就每4个一组，高位不足3位的补0，然后将每组依次转换成对应的十进制，得到的结果就是对应的8进制或者16进制。

二进制10101100101转八进制：2545

二进制10101100101转十六进制：565

三. 原码、反码、补码

在计算机中，最小的单位是位，也称为比特（bit）。而另一个常用单位是字节，一个字节是8位，也就是8比特，所以我们常用的二进制表示法是8位。

原码

原码是一种非常常见的二进制表示形式。在原码中，为了区别正数和负数，将二进制中的最高位作为符号位，如果是0表示正数，如果是1表示负数。

举个栗子：

0000 0001   // 表示 1
1000 0001   // 表示 -1

反码

不知道大家有没有注意到原码的一个问题，那就是负数参与计算的时候，比如

出现了一个大问题，就是1 + (-1) 不等于0，而等于 -2。

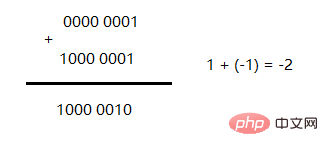
这可咋整？

Afin de résoudre ce problème, les prédécesseurs des ordinateurs intelligents ont mis au point le code d'inversion. La règle pour convertir le code original en code inverse est la suivante : Le code inverse d'un nombre positif est lui-même, le code inverse d'un nombre négatif est que le bit de signe reste inchangé et les autres bits sont inversés. La règle de la négation est que si c'est 0, ça devient 1, et si c'est 1, ça devient 0.
Jetons un coup d'œil au calcul de conversion en code inverse :

Le résultat est 1111 1111.

Hé ? Ce n'est pas vrai, pourquoi n'est-ce pas 0 ?

Ne vous inquiétez pas, ce n'est que le résultat du calcul du code inverse. Nous convertissons le code inverse en code original 1111 1111 —> le résultat attendu et résout également le calcul de la question du code d'origine.

Code complémentaire

anticode résout le problème du calcul des nombres négatifs, mais il y a encore un problème qui n'a pas été résolu, qui est -0 . En raison de l'existence du bit de signe du bit le plus élevé d'un nombre négatif, le nombre binaire original de huit bits peut représenter 2 à la puissance 8, soit 256 nombres. Cependant, l'utilisation du code original et du code complémentaire ne peut être effectuée que. représente 255, ce qui est très inconfortable pour nous, alors comment combler ce nombre manquant ?

Les programmeurs chauves ont également proposé la solution correspondante : le complément de code.

Règles pour convertir le code original en code complémentaire : Le code complémentaire d'un nombre positif est lui-même, le code complémentaire d'un nombre négatif est que le bit de signe reste inchangé, les chiffres restants sont inversés (c'est-à-dire deviennent le code complémentaire ) et ajoutez 1.

Par exemple :

Code original : 0000 0001, code complément : 0000 0001
Code original : 1000 0001, code complément : 1111 1111

Calculer :

Comme on peut le voir à partir de ce qui précède, utilisez le code complément Le calcul nous donne 0 (au lieu de -0), résolvant le problème d'un nombre en moins.

Dans le code complément, il est précisé que 0 est représenté par 0000 0000, et 1000 0000 est représenté par -128.

Notes

1. Le complément et le complément ne peuvent pas utiliser directement les règles de conversion binaire en décimal. Convertissez en décimal correspondant pour obtenir la taille correspondante. Vous devez d'abord convertir en code d'origine. En d'autres termes, le code original est une forme d'expression directement liée à la taille

2. Dans les systèmes informatiques, les valeurs​​sont toujours exprimées et stockées sous forme de codes complémentaires

3. Le code original, le complément et le complément des nombres positifs sont les mêmes

4. Les nombres négatifs sont inversés : le bit de signe reste inchangé, et les bits restants sont inversés

5. Les nombres négatifs sont inversés : le bit de signe est inchangé, les nombres négatifs sont inversés après avoir inversé les bits restants et ajouté un

6. Les nombres négatifs sont inversés : le bit de signe reste inchangé et les bits restants sont réduits de un

7. Les nombres négatifs sont inversés : le bit de signe reste inchangé et les bits restants sont réduits de un et inversés

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!