

Dans cet article, nous présenterons les principales utilisations de NumPy et comment il présente différents types de données (tableaux, images, texte, etc.). devenir une entrée pour le modèle d’apprentissage automatique.
Opérations arithmétiques sur les tableaux
Créons deux tableaux NumPy, appelés data et ones :

Pour calculer deux tableaux Pour l'addition, tapez simplement des données + un pour ajouter les données à la position correspondante (c'est-à-dire ajouter chaque ligne de données). Cette opération est plus concise que le code de méthode de bouclage pour lire le tableau.
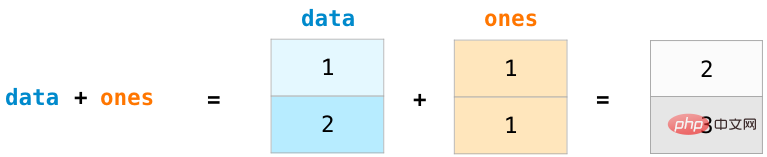
Bien sûr, sur cette base, nous pouvons également mettre en œuvre des opérations telles que la soustraction, la multiplication et la division :

Dans de nombreux cas, nous souhaitons effectuer des opérations sur des tableaux et des valeurs uniques (également appelées opérations entre vecteurs et scalaires). Par exemple : si le tableau représente la distance en miles, notre objectif est de la convertir en kilomètres. Cela peut s'écrire simplement sous forme de données * 1.6 :

NumPy sait grâce à la diffusion de tableau que cette opération nécessite de multiplier chaque élément du tableau.
Opération de découpage de tableau
Nous pouvons indexer et découper des tableaux NumPy comme les opérations de liste Python, comme indiqué ci-dessous :

Fonctions d'agrégation
Idéalement, il y a aussi des fonctions d'agrégation, qui peuvent compresser les données et compter certaines valeurs de caractéristiques dans le tableau :

En plus des fonctions telles que min, max et sum, il existe également une moyenne ( moyenne), prod (multiplication des données) calcule le produit de tous les éléments, std (écart type), etc. Tous les exemples ci-dessus concernent des vecteurs à une dimension. Au-delà de cela, un élément clé de la beauté de NumPy réside dans sa capacité à appliquer toutes les fonctions que nous avons vues jusqu'à présent à n'importe quelle dimension.
Opérations matricielles dans NumPy
De plus, vous pouvez également utiliser les ones(), les zeros() et random.random() mentionnés ci-dessus pour créer des matrices, il suffit de passer un tuple pour décrire les dimensions de la matrice :

Opérations arithmétiques sur les matrices
Pour deux matrices de même taille, on peut utiliser des opérateurs arithmétiques (+-*/) pour les additionner ou les multiplier . NumPy utilise des opérations par position pour de telles opérations :
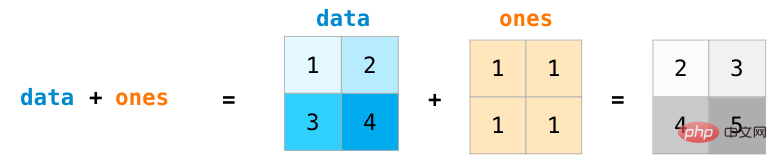
Pour des matrices de tailles différentes, nous ne pouvons effectuer ces opérations arithmétiques que lorsque les dimensions des deux matrices sont identiques à 1 (par exemple, la matrice n'a qu'une seule colonne ou une seule ligne). Dans ce cas, NumPy utilise des règles de diffusion). (diffusion) pour le traitement des opérations :

Une grande différence avec les opérations arithmétiques est la multiplication matricielle à l'aide du produit scalaire. NumPy fournit la méthode dot(), qui peut être utilisée pour effectuer des opérations de produits scalaires entre matrices :

Les dimensions de la matrice sont ajoutées au bas de la figure ci-dessus pour souligner que les deux les matrices de l'opération sont dans la colonne et les lignes doivent être égales. Cette opération peut être schématisée ainsi :

Découpage et agrégation de matrices
Les fonctions d'indexation et de découpage deviennent plus utiles lors de la manipulation de matrices. Les données peuvent être découpées à l'aide d'opérations d'index sur différentes dimensions.
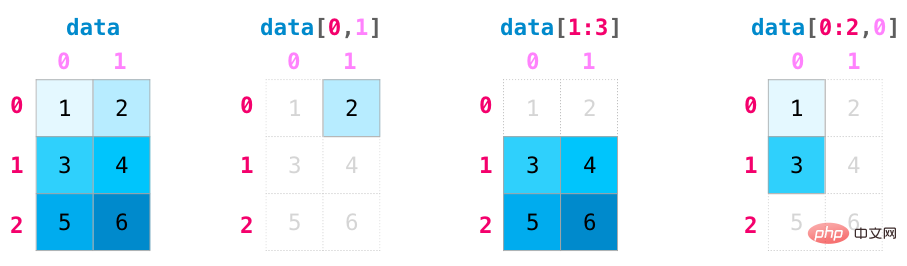
Nous pouvons agréger des matrices tout comme nous agrégeons des vecteurs :

Non seulement nous pouvons agréger le tout dans la valeur matricielle, vous pouvez également précisez-le à l'aide du paramètre axis Agrégation de lignes et de colonnes :

Transposition et reconstruction de matrices
Lors du traitement de matrices, il est souvent nécessaire de transposer la matrice. Une situation courante consiste à calculer le produit scalaire de deux matrices. La propriété T d'un tableau NumPy peut être utilisée pour obtenir la transposée d'une matrice.
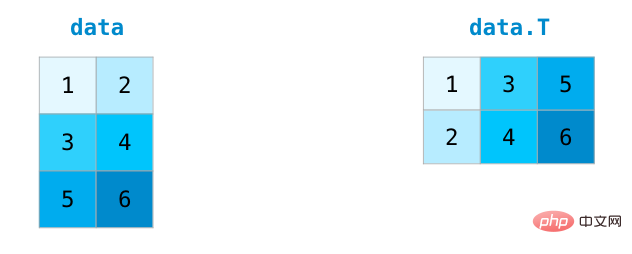
Dans des cas d'utilisation plus complexes, vous devrez peut-être modifier les dimensions d'une matrice. Ceci est courant dans les applications d'apprentissage automatique, par exemple, si la forme de la matrice d'entrée du modèle est différente de l'ensemble de données, vous pouvez utiliser la méthode reshape() de NumPy. Transmettez simplement les nouvelles dimensions requises de la matrice. Vous pouvez également passer -1 et NumPy peut déduire les dimensions correctes en fonction de votre matrice :
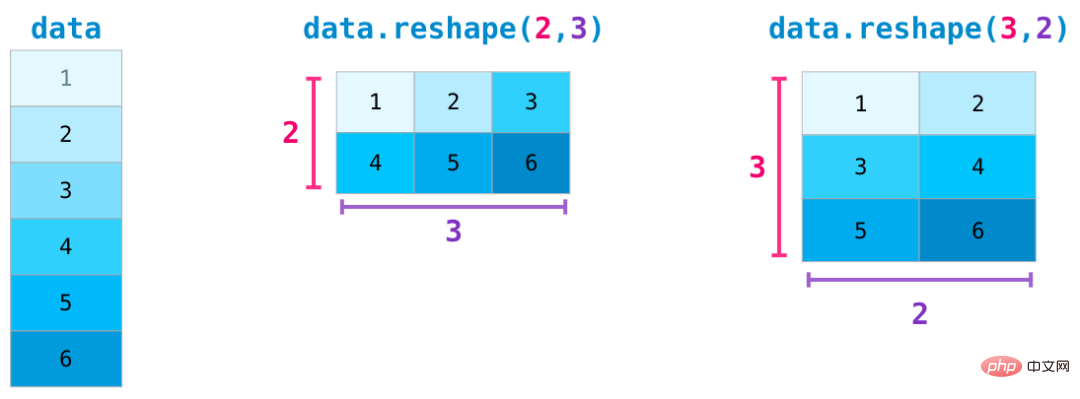
Toutes les fonctions ci-dessus sont applicables aux données multidimensionnelles, et sa structure de données centrale est appelée ndarray (tableau à N dimensions).

Souvent, changer la dimension consiste simplement à ajouter une virgule au paramètre de la fonction NumPy, comme indiqué ci-dessous :
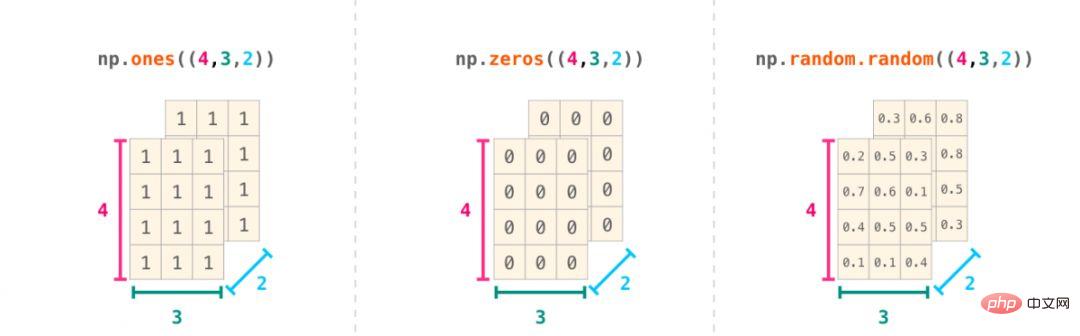
Un cas d'utilisation clé de NumPy consiste à implémenter des formules mathématiques qui fonctionnent avec des matrices et des vecteurs. C'est aussi la raison pour laquelle NumPy est couramment utilisé en Python. Par exemple, l'erreur quadratique moyenne est au cœur des modèles d'apprentissage automatique supervisés pour traiter les problèmes de régression :
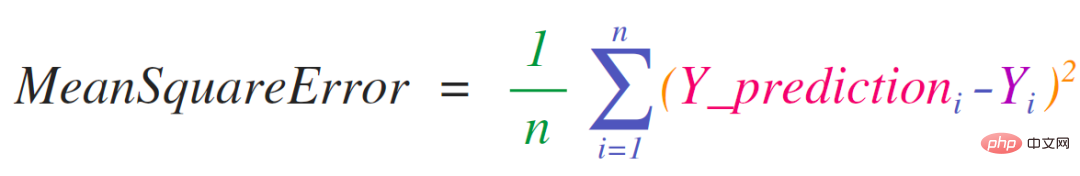
L'erreur quadratique moyenne peut être facilement implémentée dans NumPy :

L'avantage de ceci est que numpy n'a pas besoin de prendre en compte les valeurs spécifiques contenues dans les prédictions et les étiquettes. DigestBacteria passera en revue les quatre opérations de la ligne de code ci-dessus à travers un exemple :

Les vecteurs de prédictions et d'étiquettes contiennent trois valeurs. Cela signifie que la valeur de n est 3. Après avoir effectué la soustraction, on se retrouve avec des valeurs comme celle-ci :

On peut alors calculer le carré de chaque valeur dans le vecteur :

Maintenant, nous additionnons ces valeurs :

pour enfin obtenir la valeur d'erreur et le score de qualité du modèle pour cette prédiction.
quotidiennement Comment représenter les types de données avec lesquelles vous entrez en contact, telles que des feuilles de calcul, des images, de l'audio, etc. ? Numpy peut résoudre ce problème.
Tableaux et feuilles de calcul
Les feuilles de calcul ou les feuilles de données sont toutes deux des matrices bidimensionnelles. Chaque feuille de calcul de la feuille de calcul peut être sa propre variable. Une structure similaire en Python est le dataframe pandas, qui est en fait construit à l'aide de NumPy.
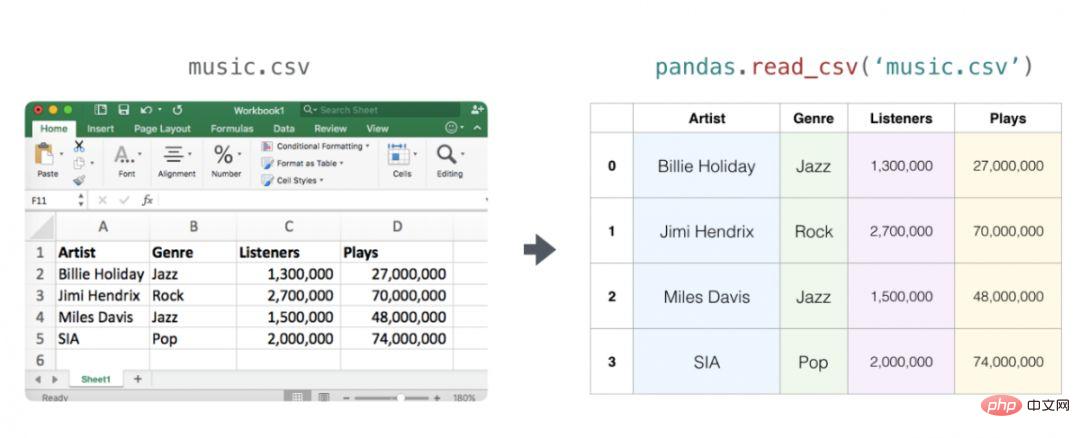
Audio et séries temporelles
Les fichiers audio sont des tableaux unidimensionnels d'échantillons. Chaque échantillon est un nombre qui représente un petit segment du signal audio. L'audio de qualité CD peut contenir 44 100 échantillons par seconde, chaque échantillon étant un nombre entier compris entre -65 535 et 65 536. Cela signifie que si vous disposez d'un fichier WAVE de qualité CD de 10 secondes, vous pouvez le charger dans un tableau NumPy d'une longueur de 10 * 44 100 = 441 000 échantillons. Vous souhaitez extraire la première seconde de l'audio ? Chargez simplement le fichier dans un tableau NumPy que nous appelons audio et interceptons l'audio[:44100].
Ce qui suit est un fichier audio :
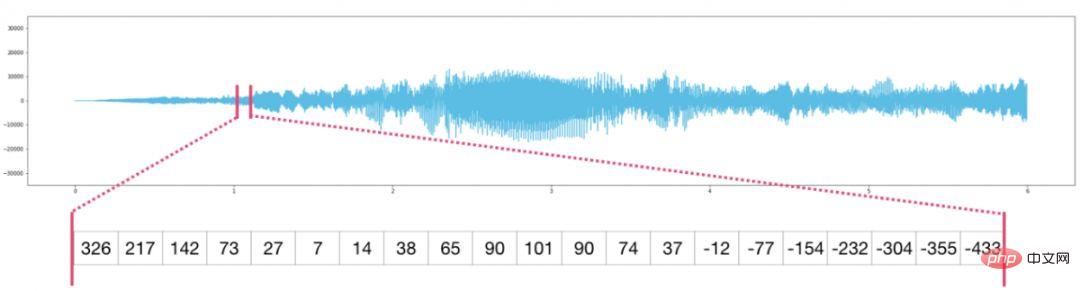
Il en va de même pour les données de séries chronologiques (par exemple, une séquence de cours boursiers au fil du temps).
Image
Une image est une matrice de pixels de taille (hauteur × largeur). Si l'image est en noir et blanc (également appelée image en niveaux de gris), chaque pixel peut être représenté par un seul nombre (généralement entre 0 (noir) et 255 (blanc)). Si vous traitez une image, vous pouvez recadrer une zone de 10 x 10 pixels dans le coin supérieur gauche de l'image en utilisant image[:10,:10] dans NumPy.
Ceci est un extrait d'un fichier image :
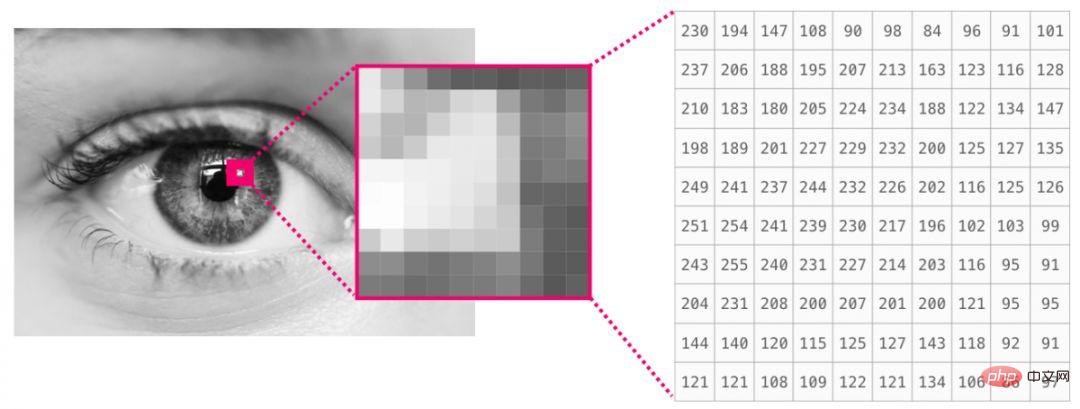
Si l'image est en couleur, chaque pixel est représenté par trois nombres : rouge, vert et bleu. Dans ce cas, nous avons besoin d’une troisième dimension (puisque chaque cellule ne peut contenir qu’un seul nombre). L'image couleur est donc représentée par un ndarray de dimensions (hauteur x largeur x 3).

Langue
Les choses sont différentes si nous traitons du texte. La représentation numérique d'un texte nécessite deux étapes : la création d'un vocabulaire (une liste de tous les mots uniques connus du modèle) et l'intégration. Regardons les étapes pour représenter numériquement cette citation ancienne (traduite) : « Les bardes qui m'ont précédé ont-ils laissé un thème méconnu
Le modèle doit être formé sur une grande quantité de texte avant de pouvoir le faire ? représenter numériquement les vers du poète de ce champ de bataille. Nous pouvons laisser le modèle traiter un petit ensemble de données et utiliser cet ensemble de données pour construire un vocabulaire (71 290 mots) :

La phrase peut ensuite être divisée en une série de jetons "mots" (mots ou parties de mots basés sur des règles communes) :

Ensuite, nous remplaçons chaque mot par son identifiant du vocabulaire :

Ces identifiants ne fournissent toujours pas d'informations précieuses au modèle. Par conséquent, avant d'introduire une séquence de mots dans le modèle, le jeton/mot doit être remplacé par une intégration (dans ce cas, en utilisant une intégration word2vec à 50 dimensions) :

Vous pouvez voir que les dimensions de ce tableau NumPy sont [embedding_dimension x séquence_length].
En pratique, ces valeurs ne ressemblent pas forcément à ceci, mais je les présente ainsi par souci de cohérence visuelle. Pour des raisons de performances, les modèles d'apprentissage profond ont tendance à conserver la première dimension de la taille du lot (car le modèle peut être entraîné plus rapidement si plusieurs exemples sont entraînés en parallèle). Évidemment, c'est un bon endroit pour utiliser reshape(). Par exemple, un modèle comme BERT s'attendrait à ce que sa matrice d'entrée ait la forme : [batch_size, séquence_length, embedding_size].
Il s'agit d'une collection de nombres que les modèles peuvent traiter et effectuer diverses opérations utiles. J'ai laissé de nombreuses lignes vides qui peuvent être remplies avec des exemples supplémentaires pour la formation (ou la prédiction) du modèle.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!