Comment confirmer en Java si quatre points donnés forment un carré ?

Un carré est une forme bidimensionnelle avec quatre côtés de même longueur. Les côtés opposés d’un carré sont parallèles, les quatre angles intérieurs sont des angles droits et les diagonales sont de même longueur. Dans cet article, nous examinerons comment confirmer si quatre points donnés forment un carré.

Nous obtiendrons un carré avec quatre points, à savoir A, B, C, D, comme indiqué sur l'image −

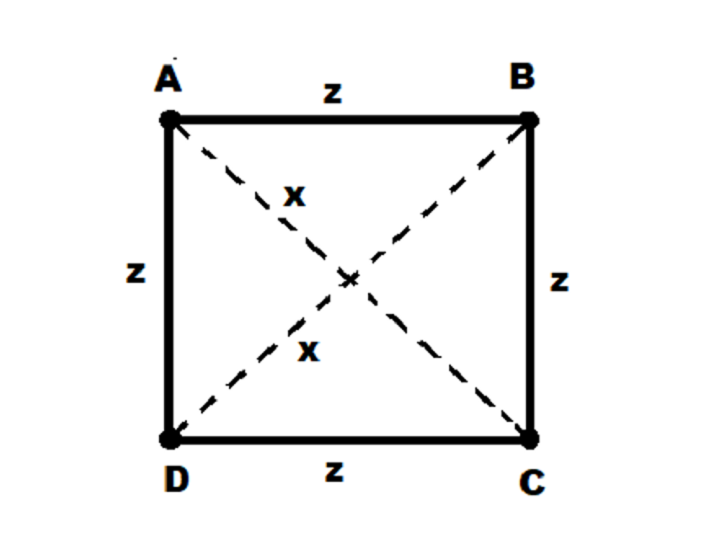
Nous devons vérifier à partir de ces points s’ils forment un carré. Afin de vérifier cela, il doit satisfaire aux conditions suivantes −

• La distance entre le point A et le point C, et la distance entre le point B et le point D, c'est-à-dire "x" doivent être égales.

• La distance entre le point A et le point B, la distance entre le point B et le point C, la distance entre le point C et le point D, la distance entre le point D et le point A, c'est-à-dire "z" doit être égale.

Nous trouverons la distance entre deux points en utilisant la formule -

$$mathrm{d=sqrt{(x_{2}-x_{1})^2(y_{2}-y_{1})^2}}$$

Le point 1 sera (x1, y1) et le point 2 sera (x2, y2).

Commençons !

Montrez quelques exemples

La traduction chinoise de

Instance-1

est :

Instance-1

• Étant donné que quatre points d'entrée sont -

• P1(3,7), P2(4,3), P3(7,8), P4(1,9)

• Mettez-le dans la formule de distance et vérifiez si la condition du carré est remplie, le résultat sera -

• Étant donné que quatre points ne forment pas un carré.

Exemple-2

• Étant donné que quatre points d'entrée sont -

• P1(20,20), P2(20,10), P3(10,10), P4(10,20)

• Mettez-le dans la formule de distance et vérifiez si la condition du carré est remplie, le résultat sera -

• Étant donné que quatre points forment un carré.

Algorithme

• Étape 1 - Déclarez et initialisez les variables.

• Étape 2 - Trouvez la distance entre le centre 1 et le centre 2 du cercle.

• Étape 3 - Vérifiez les cinq conditions de distance.

• Étape 4 − Imprimez le résultat.

Plusieurs méthodes

Nous proposons des solutions de différentes manières.

• En utilisant une entrée statique

• En utilisant des méthodes définies par l'utilisateur

Regardons le programme et sa sortie un par un.

Méthode 1 : Utiliser la saisie statique

Dans cette méthode, des valeurs en points seront attribuées. Ensuite, selon l'algorithme, nous découvrirons si les quatre points donnés forment un carré.

La traduction chinoise de

Exemple

est :

Exemple

public class Main{
   
   //main method
   public static void main(String[] args){
      
      //declaring variables
      int x1=3, x2=4, x3=7, x4=1;
      int y1=7, y2=3, y3=8, y4=9;
      double d1, d2, d3, d4, d5, d6;

      //applyinng logic
      d1 = (x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1);
      d2 = (x3 - x2) * (x3 - x2) + (y3 - y2) * (y3 - y2);
      d3 = (x4 - x3) * (x4 - x3) + (y4 - y3) * (y4 - y3);
      d4 = (x1 - x4) * (x1 - x4) + (y1 - y4) * (y1 - y4);
	   d5 = (x4 - x2) * (x4 - x2) + (y4 - y2) * (y4 - y2);
      d6 = (x3 - x1) * (x3 - x1) + (y3 - y1) * (y3 - y1);  
      
      if (d1 == 0 || d2 == 0 || d3 == 0 || d4 == 0 || d5 == 0 || d6 == 0){
		   System.out.println("Given four points do not form a square");
      }
      else if (d1 == d2 && d2 == d3 && d3 == d4 && d5 == d6){
	      
         //prints if four points form square
	      System.out.println("Given four points form a square");
	   } else {
	      
         //prints if four points do not form square 
	      System.out.println("Given four points do not form a square");
	   }

	}
} 

Sortie

Given four points do not form a square

Méthode 2 : Utiliser des méthodes définies par l'utilisateur

Dans cette méthode, des valeurs en points seront attribuées. Ensuite, une méthode définie par l'utilisateur est appelée en transmettant la valeur donnée et, sur la base de l'algorithme, elle détermine si les quatre points donnés forment un carré.

La traduction chinoise de

Exemple

est :

Exemple

public class Main{

   //main method
   public static void main(String[] args){
   
      //creating objects of Point
      Point p1 = new Point(20, 20);
      Point p2 = new Point( 20, 10 );
      Point p3 = new Point(10, 10 );
      Point p4 = new Point( 10, 20 );

      //calling user defined method
      if(isSquare(p1, p2, p3, p4)==true){
      
         //print if four points form a square
         System.out.println("Given four points form a square");   
      }
      else{
         
         //print if points does not form a square
         System.out.println("Given four points do not form a square"); 
      }
   }

   // Declaring Point class
   static class Point{
      int x, y;
      public Point(int x, int y){
         this.x = x;
         this.y = y;
      }
   };

   //function to find square of distance from point 'p' to point 'q'
   static int distSq(Point p, Point q){
      return (p.x - q.x) * (p.x - q.x) + (p.y - q.y) * (p.y - q.y);
   }

   //user defined method
   static boolean isSquare(Point p1, Point p2, Point p3, Point p4){
      int d1 = distSq(p1, p2); 
      int d2 = distSq(p2, p3); 
      int d3 = distSq(p3, p4);
      int d4 = distSq(p4, p1);
	
      int d5 = distSq(p1, p3);
      int d6 = distSq(p2, p4);
      if (d1 == 0 || d2 == 0 || d3 == 0 || d4 == 0 || d5 == 0 || d6 == 0)
         return false;

      if (d1 == d2 && d2 == d3 && d3 == d4 && d5 == d6){
	   
         //it returns true if (p1, p2, p3, p4) form a square
         return true;
      }

      //it returns false if (p1, p2, p3, p4) do not form a square
      return false;
   }
}

Sortie

Given four points form a square

Dans cet article, nous explorons différentes façons de vérifier si une ligne touche, coupe ou se trouve à l'extérieur d'un cercle à l'aide du langage de programmation Java.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!