 développement back-end
développement back-end
 C++
C++
 Nombre de chemins de la racine aux feuilles avec au plus M nœuds consécutifs et valeur K
Nombre de chemins de la racine aux feuilles avec au plus M nœuds consécutifs et valeur K
Nombre de chemins de la racine aux feuilles avec au plus M nœuds consécutifs et valeur K
Présentation
L'arbre binaire est une structure de données fascinante avec un large éventail d'applications en informatique et en programmation. Un problème intéressant consiste à trouver le décompte d’un arbre donné composé d’un nœud parent et de ses enfants. Un arbre binaire est composé de nœuds, le nœud racine est déterminé et le nœud racine peut fournir des nœuds enfants en fonction des besoins de l'utilisateur. La valeur K est déterminée et la méthode de mouvement est sélectionnée par la valeur M.
Nombre de chemins racine à feuille
Le graphique est créé à l'aide de divers nœuds contenant des valeurs sous forme d'entiers. Cet article se concentre principalement sur le comptage depuis le nœud de départ ou le nœud racine jusqu'au nœud feuille ou au nœud enfant.
Exemple
Le graphique est créé à partir d'un arbre binaire avec différents nœuds.
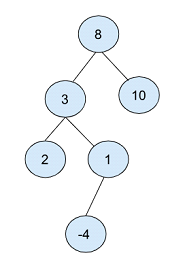
Dans l'arbre binaire ci-dessus, le nœud racine est sélectionné comme "8".
Créez ensuite deux nœuds, l'un avec une valeur de 3 et l'autre avec une valeur de 10, occupant les positions gauche et droite du nœud racine.
En prenant le nœud de valeur 2 comme racine, créez un autre nœud enfant avec les valeurs 2 et 1 comme nœuds gauche et droit respectivement.
Enfin, le nœud enfant de valeur 1 crée un nœud enfant de valeur -4.
Méthode 1 : code C++ pour calculer un chemin racine à feuille composé de jusqu'à M nœuds consécutifs avec K valeurs à l'aide d'une fonction récursive
Pour résoudre ce problème efficacement, nous utiliserons des concepts de base tels que l'algorithme de traversée d'arbre et la récursivité.
Algorithme
Étape 1 : Créez une structure pour représenter le nœud de l'arbre, qui comprend deux pointeurs (nœud enfant gauche et nœud enfant droit) et un champ entier pour stocker la valeur du nœud.
Étape 2 : Concevoir une fonction récursive pour parcourir l'arbre binaire en commençant par la racine, tout en suivant la longueur actuelle du chemin (initialisée à 0), le nombre d'occurrences consécutives (initialement définie à 0), la valeur cible K et le nombre maximum autorisé d'occurrences consécutives M .
Étape 3 : Appelez la fonction de manière récursive sur chaque sous-arbre gauche et droit, en transmettant des paramètres mis à jour tels que la longueur du chemin incrémentiel et le nombre d'occurrences consécutives (le cas échéant).
Étape 4 : Pour chaque nœud non vide visité lors du parcours :
a) Si sa valeur est égale à K, ajoutez un aux deux variables.
b) Remettez la variable à zéro si sa valeur ne correspond pas à K ou dépasse le nombre d'occurrences consécutives de M qui ont été rencontrées jusqu'à présent dans le chemin.
Étape 5 : Lors de la traversée de l'arbre, si la valeur d'un nœud enfant est nulle dans les cas gauche et droit, nous pouvons le gérer de deux manières, c'est-à-dire :
a) Vérifiez si la variable ne dépasse pas M.
b) Si oui, augmentez de 1 le nombre total de chemins qui satisfont à la condition.
Exemple
//including the all in one header
#include<bits/stdc++.h>
using namespace std;
//creating structure with two pointers as up and down
struct Vertex {
int data;
struct Vertex* up;
struct Vertex* down;
};
//countPaths function declared with five arguments ; with root = end; Node= vertex; left = up; right = down
int countPaths(Vertex* end, int K, int M, int currCount, int
consCount) {
//To check the condition when the root is equal to 1 and greater than the maximum value, the values is incremented
if (end == NULL || consCount > M) {
return 0;
}
//To check when the root is equal to the K value, increment by 1
if (end->data == K) {
currCount++;
consCount++;
} else {
//If it is not equal, it will return 0
currCount = 0;
}
if (end->up == NULL && end->down == NULL) {
if (currCount <= M) {
return 1;
} else {
return 0;
}
}
return countPaths(end->up, K, M, currCount, consCount) + countPaths(end->down, K, M, currCount, consCount);
}
//Main function to test the implementation
int main() {
Vertex* end = new Vertex();
end->data = 8;
end->up = new Vertex();
end->up->data = 3;
end->down = new Vertex();
end->down->data = 10;
end->up->up = new Vertex();
end->up->up->data = 2;
end->up->down = new Vertex();
end->up->down->data = 1;
end->up->down->up = new Vertex();
end->up->down->up->data = -4;
int K = 1; // Value of node
int M = 2; // Maximum consecutive nodes
int currCount = -1; // Current count
int consCount = -1; // Consecutive count
cout << "The number of paths obtained from the given graph of" << M << "nodes with a value of " << K << " is " << countPaths(end, K, M, currCount, consCount) << endl;
return 0;
}
Sortie
The number of paths obtained from the given graph of 2 nodes with a value of 1 is 3
Conclusion
Dans cet article, nous explorons le problème du comptage du nombre de chemins depuis le sommet (c'est-à-dire la feuille) jusqu'à la pointe ou la racine. De tels problèmes peuvent être résolus efficacement en utilisant des algorithmes de traversée d’arbres et des techniques récursives en C++. Le processus de parcours d’un arbre binaire peut sembler difficile, mais cela devient facile avec des exemples.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Qu'est-ce qu'une valeur de hachage MD5 ?
Feb 18, 2024 pm 08:50 PM
Qu'est-ce qu'une valeur de hachage MD5 ?
Feb 18, 2024 pm 08:50 PM
Quelle est la valeur MD5 ? En informatique, MD5 (MessageDigestAlgorithm5) est une fonction de hachage couramment utilisée pour digérer ou chiffrer des messages. Il produit un nombre binaire de 128 bits de longueur fixe, généralement représenté en hexadécimal 32 bits. L'algorithme MD5 a été conçu par Ronald Rivest en 1991. Bien que l’algorithme MD5 ne soit plus considéré comme sécurisé dans le domaine de la cryptographie, il est encore largement utilisé dans la vérification de l’intégrité des données et des fichiers.
 Analyse des valeurs PHP : Explication détaillée du concept et de l'application des valeurs en PHP
Mar 21, 2024 pm 09:06 PM
Analyse des valeurs PHP : Explication détaillée du concept et de l'application des valeurs en PHP
Mar 21, 2024 pm 09:06 PM
Analyse de la valeur PHP : explication détaillée du concept et de l'application de la valeur en PHP Dans la programmation PHP, la valeur est un concept très basique et important. Dans cet article, nous approfondirons le concept de valeurs en PHP et son application dans la programmation du monde réel. Nous analyserons en détail les types de valeurs de base, les variables, les tableaux, les objets et les constantes, etc., et fournirons des exemples de code spécifiques pour aider les lecteurs à mieux comprendre et utiliser les valeurs en PHP. Types de valeurs de base En PHP, les types de valeurs de base les plus courants incluent les entiers, les virgules flottantes, les chaînes, les booléens et les valeurs nulles. Ces bases
 Explorez les valeurs inadressables dans Go
Mar 25, 2024 am 09:33 AM
Explorez les valeurs inadressables dans Go
Mar 25, 2024 am 09:33 AM
Dans le langage Go, certaines valeurs ne sont pas adressables, c'est-à-dire que leurs adresses mémoire ne peuvent pas être obtenues. Ces valeurs incluent des constantes, des littéraux et des expressions qui ne peuvent pas être traitées. Dans cet article, nous allons explorer ces valeurs non adressables et comprendre leurs caractéristiques à travers des exemples de code concrets. Tout d’abord, regardons quelques exemples de constantes. Dans le langage Go, les constantes ne sont pas adressables car leurs valeurs sont déterminées au moment de la compilation et il n'y a pas d'adresse mémoire d'exécution pour l'accès. Voici un exemple de code : packagemaini
 Programmation en C++, trouver le nombre de chemins d'un point à un autre dans une grille
Aug 29, 2023 pm 10:25 PM
Programmation en C++, trouver le nombre de chemins d'un point à un autre dans une grille
Aug 29, 2023 pm 10:25 PM
Dans cet article, nous sommes confrontés à un problème dans lequel nous devons trouver le nombre total de chemins du point A au point B, où A et B sont des points fixes, c'est-à-dire A est le point du coin supérieur gauche de la grille et B est le point inférieur. point du coin droit, par exemple −Input:N=5Output:252Input:N=4Output:70Input:N=3Output:20 Dans le problème donné, nous pouvons formaliser la réponse et dériver le résultat à travers des observations simples. Méthode de recherche de solution Dans cette méthode, nous dérivons une formule en observant que lorsque nous traversons la grille de A à B, nous devons aller à droite n fois et descendre n fois, ce qui signifie que nous devons trouver toutes les combinaisons de chemins possibles, nous obtenons donc
 Classe facultative dans Java 8 : Comment filtrer les valeurs éventuellement nulles à l'aide de la méthode filter()
Aug 01, 2023 pm 05:27 PM
Classe facultative dans Java 8 : Comment filtrer les valeurs éventuellement nulles à l'aide de la méthode filter()
Aug 01, 2023 pm 05:27 PM
Classe facultative en Java8 : Comment utiliser la méthode filter() pour filtrer les valeurs éventuellement nulles En Java8, la classe facultative est un outil très utile qui nous permet de mieux gérer les valeurs éventuellement nulles et d'éviter l'apparition de NullPointerException. La classe Optionnel fournit de nombreuses méthodes pour manipuler les valeurs nulles potentielles, l'une des méthodes importantes est filter(). La fonction de la méthode filter() est que si Option
 Trouver le nombre de chemins de poids W dans un arbre K-ary en utilisant C++
Sep 16, 2023 pm 06:09 PM
Trouver le nombre de chemins de poids W dans un arbre K-ary en utilisant C++
Sep 16, 2023 pm 06:09 PM
Dans cet article, nous utiliserons C++ pour compter le nombre de chemins de poids W dans un arbre K-ary. On nous a donné un arbre K-ary, qui est un arbre dans lequel chaque nœud a K enfants et chaque arête a un poids, le poids décroissant de 1 à K d'un nœud à tous ses enfants. Nous devons compter le nombre cumulé de chemins partant du nœud racine qui ont un poids W et au moins une arête de poids M. Voici donc un exemple : Input:W=4,K=3,M=2Output:6 Dans le problème donné, nous utiliserons dp pour réduire la complexité temporelle et spatiale. En utilisant la mémorisation, nous pouvons rendre nos programmes plus rapides et les adapter à des contraintes plus larges. Méthode Dans cette méthode, nous allons parcourir l'arbre et garder une trace des utilisations
 Découvrez le charme de Java Map et résolvez les problèmes de traitement des données
Feb 19, 2024 pm 07:03 PM
Découvrez le charme de Java Map et résolvez les problèmes de traitement des données
Feb 19, 2024 pm 07:03 PM
Explication de Map Map est une structure de données qui vous permet de stocker des paires clé-valeur. Les clés sont uniques et les valeurs peuvent être n'importe quel type d'objet. L'interface Map fournit des méthodes pour stocker et récupérer des paires clé-valeur et vous permet de parcourir les paires clé-valeur dans la carte. Types de Map Il existe plusieurs implémentations différentes de Map en Java, les plus courantes sont HashMap, TreeMap et LinkedHashMap. HashMap : implémentation de carte basée sur une table de hachage, qui présente les caractéristiques d'une recherche, d'une insertion et d'une suppression rapides, mais elle n'est pas ordonnée, ce qui signifie que l'ordre des paires clé-valeur dans la carte est arbitrairement déterminé. TreeMap : une implémentation de carte basée sur des arbres rouge-noir, avec les caractéristiques de recherche, d'insertion et de suppression rapides, et elle est
 Que se passe-t-il lors de la conversion d'une valeur en booléen en JavaScript ?
Sep 02, 2023 am 09:21 AM
Que se passe-t-il lors de la conversion d'une valeur en booléen en JavaScript ?
Sep 02, 2023 am 09:21 AM
Convertissez en valeur booléenne à l'aide de la méthode Boolean() en JavaScript. Vous pouvez essayer d'exécuter le code suivant pour comprendre comment convertir [50,100] en booléen en JavaScript. Exemple de démonstration en temps réel<!DOCTYPEhtml><html> <body> <p>Convert[50,100]toBoolean</p> &





