 développement back-end
développement back-end
 C++
C++
 Programme C pour trouver le nombre minimum de sauts pour arriver à la fin
Programme C pour trouver le nombre minimum de sauts pour arriver à la fin
Programme C pour trouver le nombre minimum de sauts pour arriver à la fin

Étant donné un tableau d'entiers non négatifs, représentant le nombre maximum Mesures qui peuvent être prises à partir de cet élément. Le pointeur est initialement situé au premier index [index 0] du tableau. Votre objectif est d'atteindre la fin L'index dans le tableau en un nombre minimum d'étapes. si inaccessible fin du tableau, puis imprime le plus grand entier.
L'approche naïve consiste à commencer par le composant {main} initial et à appeler récursivement tous les composants accessibles à partir du premier élément. La portée minimale de saut du premier à la fin est calculée en utilisant la portée minimale de saut requise pour atteindre la fin à partir du premier élément accessible.
minJumps(start, end) = Min ( minJumps(k, end) ) for all k accessible from the start
Ici, nous utiliserons une approche de programmation dynamique descendante. Nous utiliserons Hashmap pour stocker les résultats des sous-problèmes et chaque fois que nous créerons une solution, vérifiez d'abord si le sous-problème a été résolu et si c'est le cas, utilisez-le.
Input: { 1, 2, 4, 1, 2, 2, 1, 1, 3, 8 }
Output: Minimum number of steps = 6 {1-->2-->4-->1-->3-->8}Explication
Le premier élément est 1, il ne peut donc aller qu'à 2. Le deuxième élément est 2, vous pouvez donc monter jusqu'à 2 étapes, par exemple jusqu'à 4 ou 1. de la portée 1 à 4, et Et ainsi de suite.
Complexité des méthodes de programmation dynamique pour trouver des nombres minimaux Le nombre de sauts pour atteindre la fin du tableau est O(n^2), et la complexité spatiale est O(n)
Exemple
Démonstration en temps réel
#include<stdio.h>
#include<limits.h>
int min_steps (int arr[], int n){
int steps[n];
int i, j;
if (n == 0 || arr[0] == 0)
return INT_MAX;
steps[0] = 0;
for (i = 1; i < n; i++){
steps[i] = INT_MAX;
for (j = 0; j < i; j++){
if (i <= j + arr[j] && steps[j] != INT_MAX){
steps[i] = (steps[i] < (steps[j] + 1)) ? steps[i] : steps[j] + 1;
break;
}
}
}
return steps[n - 1];
}
int main (){
int arr[100];
int n;
printf ("Enter size of the array:");
scanf ("%d", &n);
printf ("Enter elements in the array:");
for (int i = 0; i < n; i++){
scanf ("%d", &arr[i]);
}
printf ("Minimum number of steps : %d", min_steps (arr, n));
return 0;
}Sortie
Enter size of array : 7 Enter elements in the array :2 1 1 5 2 1 1 Minimum number of steps : 3
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Traduisez ce qui suit en chinois : Programme C pour convertir des chiffres romains en nombres décimaux
Sep 05, 2023 pm 09:53 PM
Traduisez ce qui suit en chinois : Programme C pour convertir des chiffres romains en nombres décimaux
Sep 05, 2023 pm 09:53 PM
Vous trouverez ci-dessous un algorithme en langage C pour convertir les chiffres romains en nombres décimaux : Algorithme Étape 1 - Démarrer Étape 2 - Lire les chiffres romains au moment de l'exécution Étape 3 - Longueur : = strlen (roman) Étape 4 - Pour i = 0 à Longueur-1 Étape 4.1-switch(roman[i]) Étape 4.1.1-case'm' : &nbs
 Programme C++ pour comparer l'ordre lexicographique de deux chaînes
Sep 04, 2023 pm 05:13 PM
Programme C++ pour comparer l'ordre lexicographique de deux chaînes
Sep 04, 2023 pm 05:13 PM
La comparaison de chaînes lexicographiques signifie que les chaînes sont comparées dans l’ordre du dictionnaire. Par exemple, s'il y a deux chaînes « pomme » et « appel », la première chaîne viendra en dernier car les trois premiers caractères de « application » sont identiques. Ensuite, pour la première chaîne, le caractère est « l » et dans la deuxième chaîne, le quatrième caractère est « e ». Puisque « e » est plus court que « l », il viendra en premier si nous trions lexicographiquement. Les chaînes sont comparées lexicographiquement avant d'être arrangées. Dans cet article, nous verrons différentes techniques pour comparer lexicographiquement deux chaînes en utilisant C++. Utilisation de la fonction compare() dans les chaînes C++ L'objet C++string a une fonction compare()
 Où est l'endroit où la bougie brille dans Destiny Ark ?
Mar 20, 2024 pm 05:46 PM
Où est l'endroit où la bougie brille dans Destiny Ark ?
Mar 20, 2024 pm 05:46 PM
L'ouverture d'une nouvelle version de la nouvelle carte de l'Arche du Destin comporte également une nouvelle mission de réputation. En plus de la carte Rowan, il existe également une mission quotidienne sur Wisdom Island. La mission préalable est lancée depuis Belongnan. a atteint l'objectif de "trouver la bonne carte". Il n'y a pas de guide pour ce lien "L'endroit où brille la bougie". Je suis également curieux de connaître l'emplacement spécifique. Voici le guide pour cette tâche ! Trouver l'endroit où brille la bougie se trouve dans la pièce de l'Île de la Sagesse de l'Arche du Destin. Il y a aussi un couloir dans le hall, qui peut mener au sous-sol. Lorsque vous entrez, vous pouvez voir l'emplacement du suivant. tâches, comme le montre l'image :
 Programme C++ pour trouver la valeur de la fonction sinus hyperbolique inverse en prenant une valeur donnée comme argument
Sep 17, 2023 am 10:49 AM
Programme C++ pour trouver la valeur de la fonction sinus hyperbolique inverse en prenant une valeur donnée comme argument
Sep 17, 2023 am 10:49 AM
Les fonctions hyperboliques sont définies à l'aide d'hyperboles au lieu de cercles et sont équivalentes aux fonctions trigonométriques ordinaires. Il renvoie le paramètre de rapport dans la fonction sinus hyperbolique à partir de l'angle fourni en radians. Mais faites le contraire, ou en d’autres termes. Si nous voulons calculer un angle à partir d’un sinus hyperbolique, nous avons besoin d’une opération trigonométrique hyperbolique inverse comme l’opération sinus hyperbolique inverse. Ce cours montrera comment utiliser la fonction sinus hyperbolique inverse (asinh) en C++ pour calculer des angles en utilisant la valeur du sinus hyperbolique en radians. L'opération arc sinus hyperbolique suit la formule suivante -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Où\:In\:is\:logarithme naturel\:(log_e\:k)
 Programme C pour trouver la longueur de la liste chaînée
Sep 07, 2023 pm 07:33 PM
Programme C pour trouver la longueur de la liste chaînée
Sep 07, 2023 pm 07:33 PM
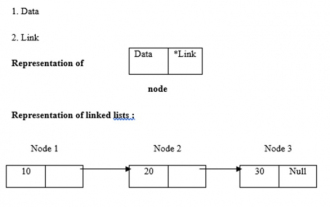
Les listes chaînées utilisent l’allocation dynamique de mémoire, c’est-à-dire qu’elles grandissent et diminuent en conséquence. Ils sont définis comme des collections de nœuds. Ici, un nœud comporte deux parties, des données et des liens. Les données, liens et listes chaînées sont représentés comme suit - Types de listes chaînées Il existe quatre types de listes chaînées, comme suit : - Liste chaînée simple / Liste chaînée simple Liste chaînée double / Double Liste chaînée simple circulaire Liste chaînée double circulaire Nous utilisons le méthode récursive pour trouver la longueur de la liste chaînée La logique est -intlength(node *temp){ if(temp==NULL) returnl{&n
 Le programme C utilise la fonction rename() pour changer le nom du fichier
Sep 21, 2023 pm 10:01 PM
Le programme C utilise la fonction rename() pour changer le nom du fichier
Sep 21, 2023 pm 10:01 PM
La fonction renommer modifie un fichier ou un répertoire de son ancien nom à son nouveau nom. Cette opération est similaire à l’opération de déplacement. Nous pouvons donc également utiliser cette fonction de renommage pour déplacer des fichiers. Cette fonction existe dans le fichier d'en-tête de la bibliothèque stdio.h. La syntaxe de la fonction rename est la suivante : intrename(constchar*oldname,constchar*newname); La fonction rename() accepte deux paramètres. L’un est l’ancien nom et l’autre le nouveau nom. Les deux paramètres sont des pointeurs vers des caractères constants qui définissent l'ancien et le nouveau nom du fichier. Renvoie zéro si le fichier a été renommé avec succès ; sinon, renvoie un entier différent de zéro. Lors d'une opération de changement de nom
 Programme C++ pour imprimer le dictionnaire
Sep 11, 2023 am 10:33 AM
Programme C++ pour imprimer le dictionnaire
Sep 11, 2023 am 10:33 AM
Une carte est un type spécial de conteneur en C++ où chaque élément est une paire de deux valeurs, à savoir une valeur clé et une valeur mappée. La valeur clé est utilisée pour indexer chaque élément et la valeur mappée est la valeur associée à la clé. Que la valeur mappée soit unique ou non, la clé est toujours unique. Pour imprimer des éléments de carte en C++, nous devons utiliser un itérateur. Un élément dans un ensemble d’éléments est indiqué par un objet itérateur. Les itérateurs sont principalement utilisés avec des tableaux et d'autres types de conteneurs (tels que des vecteurs), et ils disposent d'un ensemble spécifique d'opérations qui peuvent être utilisées pour identifier des éléments spécifiques dans une plage spécifique. Les itérateurs peuvent être incrémentés ou décrémentés pour référencer différents éléments présents dans une plage ou un conteneur. L'itérateur pointe vers l'emplacement mémoire d'un élément spécifique dans la plage. Imprimer une carte en C++ à l'aide d'itérateurs Voyons d'abord comment définir
 Écrivez un programme C qui utilise la fonction de bibliothèque strncmp pour comparer deux chaînes
Sep 09, 2023 pm 01:17 PM
Écrivez un programme C qui utilise la fonction de bibliothèque strncmp pour comparer deux chaînes
Sep 09, 2023 pm 01:17 PM
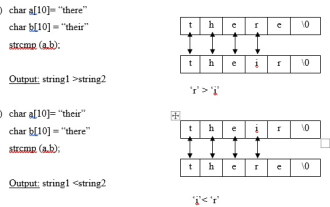
Strncmp est une fonction de bibliothèque prédéfinie, présente dans le fichier string.h, qui est utilisée pour comparer deux chaînes et afficher quelle chaîne est la plus grande. Fonction strcmp (comparaison de chaînes) Cette fonction compare deux chaînes. Il renvoie la différence ASCII du premier caractère non correspondant dans les deux chaînes. Syntaxe intstrcmp(string1,string2); Si la différence est égale à zéro, alors string1=string2. Si la différence est positive, string1>string2. Si la différence est négative, string1<string2. Exemple de fonction strncmp Cette fonction est utilisée pour comparer les n premiers caractères de deux chaînes. chaîne de syntaxe





