 développement back-end
développement back-end
 C++
C++
 À l'aide de C++, traduisez ce qui suit en chinois : Requête ET au niveau du bit dans la plage d'index d'un tableau donné
À l'aide de C++, traduisez ce qui suit en chinois : Requête ET au niveau du bit dans la plage d'index d'un tableau donné
À l'aide de C++, traduisez ce qui suit en chinois : Requête ET au niveau du bit dans la plage d'index d'un tableau donné

Dans cet article, nous sommes confrontés à un problème dans lequel, étant donné un tableau d'entiers, notre tâche est de trouver le ET au niveau du bit d'une plage donnée, par exemple
Input: arr[ ] = {1, 3, 1, 2, 32, 3, 3, 4, 4}, q[ ] = {{0, 1}, {3, 5}}
Output:
1
0 0
1 AND 31 = 1
23 AND 34 AND 4 = 00
Input: arr[ ] = {1, 2, 3, 4, 510, 10 , 12, 16, 8}, q[ ] = {{0, 42}, {1, 33, 4}}
Output:
0 8
0Nous allons d'abord appliquer la méthode de force brute et vérifier sa complexité temporelle ; Si notre complexité temporelle n’est pas suffisante, nous essayons de développer une meilleure méthode.
Méthode Brute Force
Dans la méthode donnée, nous allons parcourir la plage donnée, trouver la réponse de notre méthode et l'imprimer.
Exemple
#include <bits/stdc++.h>
using namespace std;
int main() {
int ARR[] = { 10, 10 , 12, 16, 8 };
int n = sizeof(ARR) / sizeof(int); // size of our array
int queries[][2] = { {0, 2}, {3, 4} }; // given queries
int q = sizeof(queries) / sizeof(queries[0]); // number of queries
for(int i = 0; i < q; i++) { // traversing through all the queries
long ans = 1LL << 32;
ans -= 1; // making all the bits of ans 1
for(int j = queries[i][0]; j <= queries[i][1]; j++) // traversing through the range
ans &= ARR[j]; // calculating the answer
cout << ans << "\n";
}
return 0;
}Output
8 0
Dans cette approche, nous exécutons une boucle sur chaque plage de la requête et imprimons leur ensemble au niveau du bit, de sorte que la complexité globale de notre programme devient O(N*Q ), où N est le taille du tableau et Q est le nombre de requêtes que nous avons actuellement, vous pouvez voir que cette complexité ne se prête pas à des contraintes plus élevées, nous allons donc proposer une méthode plus rapide pour ce problème.
Méthode efficace
Dans ce problème, nous pré-calculons le nombre de bits de préfixe du tableau et calculons le ET au niveau du bit de la plage donnée en vérifiant la contribution des bits définis dans la plage donnée.
Exemple
#include <bits/stdc++.h>
using namespace std;
#define bitt 32
#define MAX (int)10e5
int prefixbits[bitt][MAX];
void bitcount(int *ARR, int n) { // making prefix counts
for (int j = 31; j >= 0; j--) {
prefixbits[j][0] = ((ARR[0] >> j) & 1);
for (int i = 1; i < n; i++) {
prefixbits[j][i] = ARR[i] & (1LL << j);
prefixbits[j][i] += prefixbits[j][i - 1];
}
}
return;
}
int check(int l, int r) { // calculating the answer
long ans = 0; // to avoid overflow we are taking ans as long
for (int i = 0; i < 32; i++){
int x;
if (l == 0)
x = prefixbits[i][r];
else
x = prefixbits[i][r] - prefixbits[i][l - 1];
if (x == r - l + 1)
ans = ans | 1LL << i;
}
return ans;
}
int main() {
int ARR[] = { 10, 10 , 12, 16, 8 };
int n = sizeof(ARR) / sizeof(int); // size of our array
memset(prefixbits, 0, sizeof(prefixbits)); // initializing all the elements with 0
bitcount(ARR, n);
int queries[][2] = {{0, 2}, {3, 4}}; // given queries
int q = sizeof(queries) / sizeof(queries[0]); // number of queries
for (int i = 0; i < q; i++) {
cout << check(queries[i][0], queries[i][1]) << "\n";
}
return 0;
}Sortie
2 0
Dans cette approche, nous utilisons un temps constant pour calculer la requête, réduisant ainsi considérablement la complexité temporelle de O(N*Q) à O(N), où N est maintenant la taille du tableau donné. La procédure peut également être adaptée à des contraintes plus élevées.
Explication du code ci-dessus
Dans cette méthode, nous comptons tous les chiffres du préfixe et les stockons dans l'index. Désormais, lorsque nous calculons la requête, il nous suffit de vérifier si le nombre d'un certain bit est le même que le nombre d'éléments présents dans la plage. Si oui, nous définissons ce bit sur 1 dans x, si non, nous laissons le bit comme si n'importe quel nombre présent dans la plage donnée avait ce bit 0, donc tout le ET au niveau du bit de ce bit sera nul. Voici comment nous procédons calculer le ET au niveau du bit.
Conclusion
Dans cet article, nous avons résolu le problème de l'énumération de toutes les requêtes au niveau du bit ET dans une plage d'index donnée [L, R] sur un grand lot. Nous avons également appris un programme C++ pour résoudre ce problème et une manière complète de résoudre ce problème (normale et efficace). Nous pouvons écrire le même programme dans d'autres langages tels que C, Java, Python et d'autres langages. Nous espérons que cet article vous a été utile.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 12306 Comment vérifier l'historique des enregistrements d'achat de billets Comment vérifier l'historique des enregistrements d'achat de billets
Mar 28, 2024 pm 03:11 PM
12306 Comment vérifier l'historique des enregistrements d'achat de billets Comment vérifier l'historique des enregistrements d'achat de billets
Mar 28, 2024 pm 03:11 PM
Téléchargez la dernière version de l'application de réservation de billets 12306. C'est un logiciel d'achat de billets de voyage dont tout le monde est très satisfait. Il est très pratique d'aller où vous voulez. Il existe de nombreuses sources de billets fournies dans le logiciel. -authentification par nom pour acheter des billets en ligne. Tous les utilisateurs Vous pouvez facilement acheter des billets de voyage et des billets d'avion et profiter de différentes réductions. Vous pouvez également commencer à réserver à l'avance pour récupérer des billets. Vous pouvez réserver des hôtels ou des transferts spéciaux en voiture. Grâce à lui, vous pouvez aller où vous voulez et acheter des billets en un seul clic. Voyager est plus simple et plus pratique, ce qui rend l'expérience de voyage de chacun. plus confortable. Désormais, l'éditeur le détaille en ligne. Offre à 12306 utilisateurs un moyen de consulter l'historique des achats de billets. 1. Ouvrez Railway 12306, cliquez sur Mon dans le coin inférieur droit, puis cliquez sur Ma commande. 2. Cliquez sur Payé sur la page de commande. 3. Sur la page payante
 Comment vérifier vos diplômes universitaires sur Xuexin.com
Mar 28, 2024 pm 04:31 PM
Comment vérifier vos diplômes universitaires sur Xuexin.com
Mar 28, 2024 pm 04:31 PM
Comment vérifier mes diplômes universitaires sur Xuexin.com ? Vous pouvez vérifier vos diplômes universitaires sur Xuexin.com. De nombreux utilisateurs ne savent pas comment vérifier leurs diplômes universitaires sur Xuexin.com. Ensuite, l'éditeur vous propose un didacticiel graphique sur la façon de vérifier vos diplômes universitaires sur Xuexin.com. les utilisateurs viennent jeter un oeil ! Tutoriel d'utilisation de Xuexin.com : Comment vérifier vos diplômes universitaires sur Xuexin.com 1. Entrée Xuexin.com : https://www.chsi.com.cn/ 2. Requête sur le site Web : Étape 1 : Cliquez sur l'adresse Xuexin.com ci-dessus pour accéder à la page d'accueil Cliquez sur [Requête sur l'éducation] ; Étape 2 : Sur la dernière page Web, cliquez sur [Requête] comme indiqué par la flèche dans la figure ci-dessous. Étape 3 : Cliquez ensuite sur [Connexion au fichier de crédits académiques] sur la nouvelle page ; Étape 4 : Sur la page de connexion, saisissez les informations et cliquez sur [Connexion] ;
 Comparaison des similitudes et des différences entre MySQL et PL/SQL
Mar 16, 2024 am 11:15 AM
Comparaison des similitudes et des différences entre MySQL et PL/SQL
Mar 16, 2024 am 11:15 AM
MySQL et PL/SQL sont deux systèmes de gestion de bases de données différents, représentant respectivement les caractéristiques des bases de données relationnelles et des langages procéduraux. Cet article comparera les similitudes et les différences entre MySQL et PL/SQL, avec des exemples de code spécifiques à illustrer. MySQL est un système de gestion de bases de données relationnelles populaire qui utilise le langage de requête structuré (SQL) pour gérer et exploiter des bases de données. PL/SQL est un langage procédural unique à la base de données Oracle et est utilisé pour écrire des objets de base de données tels que des procédures stockées, des déclencheurs et des fonctions. même
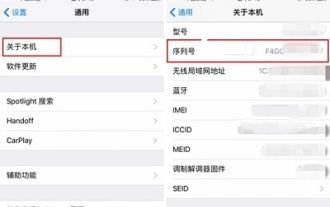 Comment vérifier la date d'activation sur le téléphone mobile Apple
Mar 08, 2024 pm 04:07 PM
Comment vérifier la date d'activation sur le téléphone mobile Apple
Mar 08, 2024 pm 04:07 PM
Si vous souhaitez vérifier la date d'activation à l'aide d'un téléphone mobile Apple, le meilleur moyen est de la vérifier via le numéro de série du téléphone mobile. Vous pouvez également la vérifier en visitant le site officiel d'Apple, en le connectant à un ordinateur et en en téléchargeant un troisième. -logiciel de fête pour le vérifier. Comment vérifier la date d'activation du téléphone mobile Apple Réponse : requête de numéro de série, requête sur le site officiel d'Apple, requête sur ordinateur, requête sur un logiciel tiers 1. La meilleure façon pour les utilisateurs est de connaître le numéro de série de leur téléphone mobile. le numéro de série en ouvrant Paramètres, Général, À propos de cette machine. 2. Grâce au numéro de série, vous pouvez non seulement connaître la date d'activation de votre téléphone mobile, mais également vérifier la version du téléphone mobile, l'origine du téléphone mobile, la date d'usine du téléphone mobile, etc. 3. Les utilisateurs visitent le site Web officiel d'Apple pour trouver une assistance technique, trouvent la colonne de service et de réparation en bas de la page et y vérifient les informations d'activation de l'iPhone. 4. Utilisateur
 Comment utiliser Oracle pour demander si une table est verrouillée ?
Mar 06, 2024 am 11:54 AM
Comment utiliser Oracle pour demander si une table est verrouillée ?
Mar 06, 2024 am 11:54 AM
Titre : Comment utiliser Oracle pour demander si une table est verrouillée ? Dans la base de données Oracle, le verrouillage de table signifie que lorsqu'une transaction effectue une opération d'écriture sur la table, les autres transactions seront bloquées lorsqu'elles souhaitent effectuer des opérations d'écriture sur la table ou apporter des modifications structurelles à la table (telles que l'ajout de colonnes, la suppression de lignes). , etc.). Dans le processus de développement actuel, nous devons souvent nous demander si la table est verrouillée afin de mieux dépanner et traiter les problèmes associés. Cet article explique comment utiliser les instructions Oracle pour demander si une table est verrouillée et donne des exemples de code spécifiques. Pour vérifier si la table est verrouillée, nous
 Partage de compétences en matière de requête de localisation de base de données Discuz
Mar 10, 2024 pm 01:36 PM
Partage de compétences en matière de requête de localisation de base de données Discuz
Mar 10, 2024 pm 01:36 PM
Le forum est l'un des formulaires de sites Web les plus courants sur Internet. Il offre aux utilisateurs une plate-forme pour partager des informations, échanger et discuter. Discuz est un programme de forum couramment utilisé, et je pense que de nombreux webmasters le connaissent déjà très bien. Lors du développement et de la gestion du forum Discuz, il est souvent nécessaire d'interroger les données de la base de données pour analyse ou traitement. Dans cet article, nous partagerons quelques conseils pour interroger l'emplacement de la base de données Discuz et fournirons des exemples de code spécifiques. Tout d’abord, nous devons comprendre la structure de la base de données de Discuz
 Comment vérifier le dernier prix du Tongshen Coin ?
Mar 21, 2024 pm 02:46 PM
Comment vérifier le dernier prix du Tongshen Coin ?
Mar 21, 2024 pm 02:46 PM
Comment vérifier le dernier prix du Tongshen Coin ? Le jeton est une monnaie numérique qui peut être utilisée pour acheter des objets, des services et des actifs dans le jeu. Il est décentralisé, ce qui signifie qu’il n’est contrôlé ni par les gouvernements ni par les institutions financières. Les transactions de Tongshen Coin sont effectuées sur la blockchain, qui est un grand livre distribué qui enregistre les informations de toutes les transactions de Tongshen Coin. Pour vérifier le dernier prix du Token, vous pouvez suivre les étapes suivantes : Choisissez un site Web ou une application de vérification des prix fiable. Certains sites Web de requête de prix couramment utilisés incluent : CoinMarketCap : https://coinmarketcap.com/Coindesk : https://www.coondesk.com/ Binance : https://www.bin
 Comment vérifier le dernier prix des pièces BitTorrent ?
Mar 06, 2024 pm 02:13 PM
Comment vérifier le dernier prix des pièces BitTorrent ?
Mar 06, 2024 pm 02:13 PM
Vérifiez le dernier prix du BitTorrent Coin (BTT) BTT est une crypto-monnaie sur la blockchain TRON qui est utilisée pour récompenser les utilisateurs du réseau BitTorrent pour le partage et le téléchargement de fichiers. Voici comment trouver le dernier prix du BTT : choisissez un site Web ou une application fiable de vérification des prix. Certains sites Web de requête de prix couramment utilisés incluent : CoinMarketCap : https://coinmarketcap.com/Coindesk : https://www.coondesk.com/Binance : https://www.binance.com/ Recherchez sur le site Web ou l'application BTT. Consultez les derniers prix du BTT. Remarque : prix des crypto-monnaies





