 développement back-end
développement back-end
 C++
C++
 Somme maximale possible du tableau après avoir effectué l'opération donnée
Somme maximale possible du tableau après avoir effectué l'opération donnée
Somme maximale possible du tableau après avoir effectué l'opération donnée

Dans cette question, nous effectuerons l'opération donnée sur les éléments du tableau et trouverons la somme maximale finale.
Ici, dans chaque opération, nous pouvons sélectionner au plus X[p] éléments du tableau et les remplacer par des éléments Y[p] pour maximiser la somme.
Dans une méthode simple, nous trouverons les éléments du tableau X[p] qui sont plus petits que les éléments Y[p] et les remplacerons par Y[p].
Dans une approche efficace, nous utiliserons la file d'attente prioritaire pour obtenir la somme maximale.
Énoncé du problème− On nous donne un tableau nums[] contenant N nombres. En même temps, on nous donne des tableaux X[] et Y[] contenant M entiers. Nous devons effectuer les opérations suivantes sur le tableau nums[].
Nous devons effectuer M opérations sur chacun des éléments X[] et Y[]. Dans chaque opération, nous devons sélectionner le plus grand élément X[p] du tableau nums[] et le remplacer par Y[p].
La tâche confiée est de trouver la somme maximale des éléments du tableau nums[] après avoir effectué M opérations.
Exemple Exemple
Entrez
nums[] = {10, 8, 7, 60, 20, 18, 30, 60}; m = 3; x[] = {1, 2, 5}; y[] = {500, 10, 2};
Sortie
708
Explication − Effectuons chaque opération une par une.
Dans la première opération, nous remplacerons 7 éléments par 500. Ainsi, le tableau devient {10, 8, 500, 60, 20, 18, 30, 60}.
Dans la deuxième opération, on peut remplacer jusqu'à 2 éléments par 10, mais on n'a qu'1 élément de moins que 10. Donc, on remplace 8 par 10 et le tableau devient {10, 10, 500, 60, 20, 18, 30, 60}.
Dans la troisième opération, nous pouvons remplacer jusqu'à 5 éléments par 2, mais il n'y a pas d'éléments inférieurs à 2 dans le tableau. Nous ne remplacerons donc aucun élément.
Entrez
nums[] = {30, 40, 50, 50, 60}; m = 3; x[] = {2, 3, 6}; y[] = {10, 8, 21};
Sortie
230
Explication − Tous les éléments du tableau y[] sont plus petits que les éléments du tableau d'origine. Par conséquent, nous n’avons besoin de remplacer aucun élément du tableau donné pour obtenir la somme maximale.
Entrez
nums[] = {30, 40, 50, 50, 60}; m = 3; x[] = {2, 4, 5}; y[] = {50, 60, 100};
Sortie
500
Explication − Ici, nous pouvons remplacer jusqu'à x[p] éléments dans chaque opération. Lors de la dernière opération, nous pouvons remplacer chaque élément du tableau par 100, ce qui donne une somme maximale égale à 100.
Méthode 1
Dans cette méthode, nous allons parcourir les tableaux x[] et y[]. À chaque itération, nous trierons le tableau pour obtenir au plus x[p] éléments du tableau qui sont plus petits que les éléments y[p] et les remplacerons par y[p].
Algorithme
Étape 1 − Initialisez « maxSum » à 0, qui est utilisé pour stocker la somme maximale des éléments du tableau.
Étape 2 − Commencez à parcourir les éléments du tableau x[] et y[].
Étape 3 − Stockez la valeur de x[p] dans une variable temporaire et triez le tableau nums[].
Étape 4− Commencez à parcourir le tableau trié dans la boucle.
Étape 5 − Si la température est supérieure à 0 et que nums[q] est inférieur à y[p], mettez à jour nums[q] avec y[p] et décrémentez la valeur de température de 1.
Étape 6− En dehors de la boucle, commencez à parcourir le tableau mis à jour, retirez la somme de tous les éléments du tableau et stockez-la dans la variable maxSum.
Étape 7 − Renvoie maxSum à la fin de la fonction.
Exemple
#include <bits/stdc++.h>
using namespace std;
int getMaxSum(int nums[], int n, int q, int x[], int y[]) {
int maxSum = 0;
// Traverse X[] and Y[] array
for (int p = 0; p < q; p++) {
// Replacing x[p] number of elements of nums[] array with y[p] if they are lesser than y[p]
int temp = x[p];
sort(nums, nums + n);
for (int q = 0; q < n; q++) {
if (temp > 0 && nums[q] < y[p]) {
nums[q] = y[p];
temp--;
}
}
}
// Sum of the array
for (int p = 0; p < n; p++) {
maxSum += nums[p];
}
return maxSum;
}
int main() {
int nums[] = {10, 8, 7, 60, 20, 18, 30, 60};
int n = (sizeof nums) / (sizeof nums[0]);
int m = 3;
int x[] = {1, 2, 5};
int y[] = {500, 10, 2};
cout << "The maximum sum we can get by replacing the array values is " << getMaxSum(nums, n, m, x, y);
return 0;
}
Sortie
The maximum sum we can get by replacing the array values is 708
Complexité temporelle− O(M*NlogN), où O(M) est utilisé pour parcourir toutes les requêtes et O(NlogN) est utilisé pour trier le tableau.
Complexité spatiale− Pour trier un tableau, la complexité spatiale est O(N).
Méthode 2
Dans cette méthode, nous utiliserons la file d'attente prioritaire pour stocker les paires d'éléments du tableau et leur nombre d'occurrences.
Par exemple, nous pousserons la paire {nums[p],1} dans la file d'attente prioritaire pour chaque élément du tableau. En même temps, nous poussons la paire {y[p], x[p]} dans la file d'attente prioritaire. Dans une file d'attente prioritaire, les paires seront triées en fonction du premier élément. Par conséquent, nous pouvons retirer les N premiers éléments de la file d’attente. Ici, pour la paire {y[p],x[p]}, nous pouvons retirer les éléments y[p] x[p] fois, et nous devons retirer un total de N éléments pour maximiser la somme.
Algorithme
Étape 1 − Initialisez le 'maxSum' avec 0 et la file d'attente prioritaire pour stocker la paire d'éléments et leur nombre d'occurrences.
Étape 2− Pour tous les éléments du tableau, insérez des paires {nums[p], 1} dans la file d'attente.
Étape 3 − Ensuite, insérez la paire {y[p], x[p]} dans la file d'attente prioritaire.
Étape 4− Répétez jusqu'à ce que n soit supérieur à 0.
Étape 4.1 − Supprimez le premier élément de la file d'attente prioritaire.
Étape 4.2 − Ajoutez first_ele * max(n, second_ele) à la somme. Ici, nous utilisons max(n, second_ele) pour gérer le dernier cas.
Étape 4.3 − Soustraire second_ele de n.
Étape 5− Renvoie maxSum.
Exemple
#include <bits/stdc++.h>
using namespace std;
int getMaxSum(int nums[], int n, int m, int x[], int y[]) {
int maxSum = 0, p;
// To get maximum sum
priority_queue<pair<int, int>> p_que;
// Insert nums[] array pairs into the queue
for (p = 0; p < n; p++)
p_que.push({nums[p], 1});
// Push replacement pairs
for (p = 0; p < m; p++)
p_que.push({y[p], x[p]});
// Add the first N elements of the priority queue in the sum
while (n > 0) {
// Get top element of priority queue
auto temp = p_que.top();
// Remove top element
p_que.pop();
// Add value to the sum
maxSum += temp.first * min(n, temp.second);
// Change N
n -= temp.second;
}
return maxSum;
}
int main() {
int nums[] = {10, 8, 7, 60, 20, 18, 30, 60};
int n = (sizeof nums) / (sizeof nums[0]);
int m = 3;
int x[] = {1, 2, 5};
int y[] = {500, 10, 2};
cout << "The maximum sum we can get by replacing the array values is " << getMaxSum(nums, n, m, x, y);
return 0;
}
Sortie
The maximum sum we can get by replacing the array values is 708
Complexité temporelle - O(N*logN + m*logm), où O(N) et O(m) sont utilisés pour parcourir le tableau donné et O(logN) sont utilisés pour insérer et supprimer des éléments dans la file d'attente.
Complexité spatiale - O(N+M) pour stocker les paires dans une file d'attente.
Dans la première méthode, nous devons trier le tableau à chaque itération pour trouver les plus petits éléments x[p]. Utilisez une file d'attente prioritaire pour trier automatiquement les éléments au fur et à mesure de leur insertion ou de leur suppression, car elle utilise la structure de données du tas. Par conséquent, cela améliore les performances de votre code.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Qu'est-ce que sudo et pourquoi est-ce important ?
Feb 21, 2024 pm 07:01 PM
Qu'est-ce que sudo et pourquoi est-ce important ?
Feb 21, 2024 pm 07:01 PM
sudo (exécution du superutilisateur) est une commande clé dans les systèmes Linux et Unix qui permet aux utilisateurs ordinaires d'exécuter des commandes spécifiques avec les privilèges root. La fonction de sudo se reflète principalement dans les aspects suivants : Fournir un contrôle des autorisations : sudo réalise un contrôle strict sur les ressources système et les opérations sensibles en autorisant les utilisateurs à obtenir temporairement les autorisations de superutilisateur. Les utilisateurs ordinaires ne peuvent obtenir des privilèges temporaires via sudo qu'en cas de besoin et n'ont pas besoin de se connecter en permanence en tant que superutilisateur. Sécurité améliorée : en utilisant sudo, vous pouvez éviter d'utiliser le compte root lors des opérations de routine. L'utilisation du compte root pour toutes les opérations peut entraîner des dommages inattendus au système, car toute opération incorrecte ou imprudente bénéficiera de toutes les autorisations. et
 Tutoriel d'utilisation de PyCharm : vous guide en détail pour exécuter l'opération
Feb 26, 2024 pm 05:51 PM
Tutoriel d'utilisation de PyCharm : vous guide en détail pour exécuter l'opération
Feb 26, 2024 pm 05:51 PM
PyCharm est un environnement de développement intégré (IDE) Python très populaire. Il fournit une multitude de fonctions et d'outils pour rendre le développement Python plus efficace et plus pratique. Cet article vous présentera les méthodes de fonctionnement de base de PyCharm et fournira des exemples de code spécifiques pour aider les lecteurs à démarrer rapidement et à maîtriser l'utilisation de l'outil. 1. Téléchargez et installez PyCharm Tout d'abord, nous devons nous rendre sur le site officiel de PyCharm (https://www.jetbrains.com/pyc
 Étapes et précautions de fonctionnement de Linux Deploy
Mar 14, 2024 pm 03:03 PM
Étapes et précautions de fonctionnement de Linux Deploy
Mar 14, 2024 pm 03:03 PM
Étapes de fonctionnement et précautions de LinuxDeploy LinuxDeploy est un outil puissant qui peut aider les utilisateurs à déployer rapidement diverses distributions Linux sur des appareils Android, permettant aux utilisateurs de découvrir un système Linux complet sur leurs appareils mobiles. Cet article présentera en détail les étapes de fonctionnement et les précautions de LinuxDeploy et fournira des exemples de code spécifiques pour aider les lecteurs à mieux utiliser cet outil. Étapes de l'opération : Installer LinuxDeploy : Tout d'abord, installez
 Que faire si vous oubliez d'appuyer sur F2 pour le mot de passe de démarrage Win10
Feb 28, 2024 am 08:31 AM
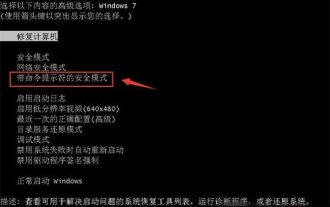
Que faire si vous oubliez d'appuyer sur F2 pour le mot de passe de démarrage Win10
Feb 28, 2024 am 08:31 AM
Vraisemblablement, de nombreux utilisateurs ont plusieurs ordinateurs inutilisés à la maison et ont complètement oublié le mot de passe de mise sous tension car ils n'ont pas été utilisés depuis longtemps. Ils aimeraient donc savoir quoi faire s'ils oublient le mot de passe ? Alors jetons un coup d’œil ensemble. Que faire si vous oubliez d'appuyer sur F2 pour le mot de passe de démarrage Win10 ? 1. Appuyez sur le bouton d'alimentation de l'ordinateur, puis appuyez sur F2 lorsque vous allumez l'ordinateur (différentes marques d'ordinateurs ont des boutons différents pour accéder au BIOS). 2. Dans l'interface du BIOS, recherchez l'option de sécurité (l'emplacement peut être différent selon les marques d'ordinateurs). Habituellement dans le menu des paramètres en haut. 3. Recherchez ensuite l’option SupervisorPassword et cliquez dessus. 4. À ce stade, l'utilisateur peut voir son mot de passe, et en même temps trouver Activé à côté et le basculer sur Dis.
 Partage des étapes d'opération de capture d'écran du Huawei Mate60 Pro
Mar 23, 2024 am 11:15 AM
Partage des étapes d'opération de capture d'écran du Huawei Mate60 Pro
Mar 23, 2024 am 11:15 AM
Avec la popularité des smartphones, la fonction capture d’écran est devenue l’une des compétences essentielles pour l’utilisation quotidienne des téléphones portables. En tant que l'un des téléphones mobiles phares de Huawei, la fonction de capture d'écran du Huawei Mate60Pro a naturellement attiré beaucoup d'attention de la part des utilisateurs. Aujourd'hui, nous partagerons les étapes de capture d'écran du téléphone mobile Huawei Mate60Pro, afin que tout le monde puisse prendre des captures d'écran plus facilement. Tout d'abord, le téléphone mobile Huawei Mate60Pro propose une variété de méthodes de capture d'écran et vous pouvez choisir la méthode qui vous convient en fonction de vos habitudes personnelles. Ce qui suit est une introduction détaillée à plusieurs interceptions couramment utilisées :
 Comment désactiver le bouton d'action sur iPhone 15 Pro et 15 Pro Max
Nov 07, 2023 am 11:17 AM
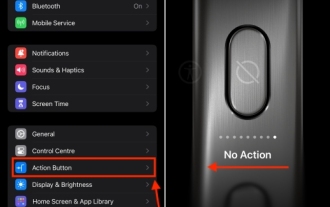
Comment désactiver le bouton d'action sur iPhone 15 Pro et 15 Pro Max
Nov 07, 2023 am 11:17 AM
Apple a apporté certaines fonctionnalités matérielles exclusives aux iPhone 15 Pro et 15 Pro Max, ce qui a attiré l’attention de tous. Nous parlons de montures en titane, de designs élégants, du nouveau chipset A17 Pro, d'un téléobjectif 5x passionnant, et bien plus encore. Parmi toutes les cloches et sifflets ajoutés aux modèles d’iPhone 15 Pro, le bouton d’action reste une fonctionnalité importante et importante. Inutile de dire que c'est un complément utile pour lancer des actions sur votre iPhone. Cela dit, vous pourriez accidentellement maintenir le bouton Action enfoncé et déclencher la fonctionnalité par inadvertance. Franchement, c'est énervant. Pour éviter cela, vous devez désactiver le bouton d'action sur les iPhone 15 Pro et 15 Pro Max. laisser
 Surveillance du défilement des pages Web CSS : surveillez les événements de défilement des pages Web et effectuez les opérations correspondantes
Nov 18, 2023 am 10:35 AM
Surveillance du défilement des pages Web CSS : surveillez les événements de défilement des pages Web et effectuez les opérations correspondantes
Nov 18, 2023 am 10:35 AM
Surveillance du défilement des pages Web CSS : surveillez les événements de défilement des pages Web et effectuez les opérations correspondantes. Avec le développement continu de la technologie frontale, les effets et les interactions des pages Web deviennent de plus en plus riches et diversifiés. Parmi eux, la surveillance du défilement est une technologie courante qui peut effectuer certains effets spéciaux ou opérations basés sur la position de défilement lorsque l'utilisateur fait défiler la page Web. D'une manière générale, la surveillance du défilement peut être implémentée via JavaScript. Cependant, dans certains cas, nous pouvons également obtenir l'effet de surveillance du défilement via du CSS pur. Cet article présentera comment implémenter le défilement des pages Web via CSS
 Boutons d'action personnalisés : explorez la personnalisation sur iPhone 15 Pro
Sep 24, 2023 pm 03:05 PM
Boutons d'action personnalisés : explorez la personnalisation sur iPhone 15 Pro
Sep 24, 2023 pm 03:05 PM
L'iPhone 15 Pro et l'iPhone 15 Pro Max d'Apple introduisent un nouveau bouton d'action programmable qui remplace le traditionnel interrupteur sonnerie/silencieux au-dessus des boutons de volume. Lisez la suite pour savoir à quoi sert le bouton Action et comment le personnaliser. Un nouveau bouton d'action sur les modèles Apple iPhone 15 Pro remplace le commutateur iPhone traditionnel qui active Ring et Silent. Par défaut, le nouveau bouton activera toujours les deux fonctions avec un appui long, mais vous pouvez également appuyer longuement pour exécuter une gamme d'autres fonctions, notamment un accès rapide à l'appareil photo ou à la lampe de poche, l'activation des mémos vocaux, le mode de mise au point, la traduction et fonctionnalités d'accessibilité telles que la loupe. Vous pouvez également l'associer à un seul raccourci, ouvrant ainsi une tonne d'autres possibilités.





