 développement back-end
développement back-end
 C++
C++
 La somme de toutes les paires de chemins les plus courts dans l'arbre
La somme de toutes les paires de chemins les plus courts dans l'arbre
La somme de toutes les paires de chemins les plus courts dans l'arbre

Dans les arbres, le terme « somme des chemins les plus courts sur toutes les paires de nœuds » fait référence au calcul de la somme des chemins les plus courts individuels pour toutes les paires de nœuds. Une méthode efficace consiste à utiliser l’algorithme double DFS (profondeur d’abord recherche). La distance entre le nœud sélectionné et tous les autres nœuds est déterminée lors du premier passage DFS. L'arbre est parcouru à nouveau lors de la deuxième passe DFS, en considérant chaque nœud comme un LCA potentiel (ancêtre commun le plus bas) et en calculant la somme des distances entre les paires de nœuds descendants du LCA sélectionné. En utilisant cette méthode, vous pouvez calculer la somme des chemins les plus courts pour toutes les paires de nœuds de l'arborescence et garantir une solution idéale.
Méthode à utiliser
Méthode Double DFS (recherche en profondeur d'abord)
Méthode de programmation dynamique
Méthode Double DFS (Depth First Search)
Pour la somme de toutes les paires de chemins les plus courts de l'arborescence, nous utilisons une méthode double DFS (profondeur d'abord recherche), qui implique deux passes DFS. Tout d’abord, nous calculons la distance entre n’importe quel nœud et tous les autres nœuds. Ensuite, lors du deuxième parcours DFS, nous parcourons l’arbre en considérant chaque nœud comme une LCA potentielle. Nous calculons et additionnons les distances entre les paires de nœuds qui sont les descendants de la LCA sélectionnée lors de la traversée. En répétant ce processus pour tous les nœuds, nous obtenons la somme de toutes les paires de chemins les plus courts. Cette stratégie est très intéressante pour ce problème car elle calcule efficacement la somme des distances entre tous les ensembles de nœuds de l'arbre.
Algorithme
N'importe quel nœud de l'arborescence peut être utilisé comme nœud de départ
Pour déterminer la distance entre le nœud de départ sélectionné et tous les autres nœuds, effectuez une recherche en profondeur d'abord (DFS) à partir de ce nœud. Ces distances doivent être enregistrées dans un tableau ou une structure de données.
Ensuite, lancez une deuxième recherche en profondeur d'abord (DFS) sur l'arbre, en considérant chaque nœud comme son éventuel ancêtre commun le plus proche (LCA)
En parcourant l'arbre lors du deuxième DFS, calculez la distance entre les paires de nœuds descendants de l'ACV sélectionnée. Pour chaque ACV, ces distances sont additionnées.
Répétez ce processus pour chaque nœud de l'arborescence
La somme de toutes les correspondances de la manière la plus finie dans l'arbre est représentée par la somme de toutes les distances calculées à l'étape 4.
Exemple
est :Exemple
#include <iostream>
#include <vector>
using namespace std;
const int MAXN = 10005;
vector<int> graph[MAXN];
int ancestor[MAXN];
int dfs(int node, int lca, int distance) {
int sum = 0;
for (int neighbor : graph[node]) {
if (neighbor != lca) {
sum += dfs(neighbor, lca, distance + 1);
}
}
return sum + distance;
}
int main() {
int lca_node = 0;
int total_sum = 0;
for (int node = 0; node < MAXN; ++node) {
if (node != lca_node) {
total_sum += dfs(node, lca_node, 0);
}
}
cout << "Total sum of distances between descendants of the LCA: " << total_sum << endl;
return 0;
}
Sortie
Total sum of distances between descendants of the LCA: 0
Méthode de programmation dynamique :
Nous sélectionnons d'abord n'importe quel nœud comme nœud racine et convertissons l'arbre en arbre enraciné dans la méthode de programmation dynamique, qui est utilisée pour calculer la somme des chemins les plus courts entre tous les nœuds de l'arbre. Nous utilisons la programmation dynamique pour calculer la répartition entre chaque nœud et le nœud racine et stockons les résultats dans un tableau. Ensuite, pour chaque nœud, nous ajoutons les séparations (calculées) de ses enfants du nœud racine pour déterminer la séparation globale de tous les autres nœuds. De cette façon, nous pouvons calculer rapidement le nombre total de chemins les plus courts entre tous les nœuds. Comme moyen efficace de résoudre ce problème, la complexité temporelle de cet algorithme est O(N), où N est le nombre de nœuds dans l’arbre.
Algorithme
Prenez n'importe quel nœud de l'arborescence comme racine et racinez l'arbre (par exemple en utilisant une recherche approfondie du nœud racine) pour créer un arbre enraciné.
La programmation dynamique peut être utilisée pour déterminer la distance de chaque nœud à la racine. Ces distances doivent être stockées dans un tableau ou une structure de données.
Calculez la somme des distances de chaque nœud à tous les autres nœuds de l'arbre :
La somme de toutes les paires de chemins les plus courts dans l'arbre est le résultat final.
a. Parcourez les nœuds enfants du nœud actuel.
b. Pour considérer le chemin passant par le nœud actuel, ajoutez le nombre de nœuds dans le sous-arbre et la distance à la racine précédemment calculée pour chaque sous-arbre.
c. Pour chaque nœud enfant du nœud actif, additionnez ces montants
d. Ajoutez le total du nœud actuel au résultat final.
#include <iostream>
#include <vector>
using namespace std;
struct TreeNode {
int val;
vector<TreeNode*> children;
};
int dfs(TreeNode* node, vector<int>& distances) {
int subtree_size = 1;
for (TreeNode* child : node->children) {
subtree_size += dfs(child, distances);
distances[node->val] += distances[child->val] + subtree_size;
}
return subtree_size;
}
int sumOfAllPairShortestPaths(TreeNode* root) {
vector<int> distances(root->val + 1, 0);
dfs(root, distances);
int total_sum = 0;
for (int distance : distances) {
total_sum += distance;
}
return total_sum;
}
int main() {
TreeNode* root = new TreeNode{0};
int result = sumOfAllPairShortestPaths(root);
cout << "Sum of all pair shortest paths in the tree: " << result << endl;
return 0;
}
Sortie
Sum of all pair shortest paths in the tree: 0
Conclusion
La somme de toutes les paires de chemins les plus courts dans l'arborescence peut être calculée à l'aide de la méthode Double DFS (Depth First Search) ou de la programmation dynamique. La méthode Double DFS consiste en deux passes, calculant d'abord la distance entre le nœud sélectionné et tous les autres nœuds, puis traversant à nouveau l'arborescence tout en traitant chaque nœud comme un ancêtre commun le plus bas (LCA) potentiel pour additionner les distances entre les paires de nœuds descendants. Les méthodes de programmation dynamique nécessitent l'utilisation récursive de DFS pour construire la racine de l'arborescence et calculer la distance entre la racine et chaque autre nœud. Le résultat des deux méthodes est le même et consiste en la somme de tous les chemins les plus courts par paire dans l’arborescence. La décision entre deux algorithmes peut être basée sur des préférences de mise en œuvre ou des structures arborescentes spécifiques, mais les deux algorithmes fournissent des solutions efficaces.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 La somme de toutes les paires de chemins les plus courts dans l'arbre
Aug 28, 2023 pm 03:17 PM
La somme de toutes les paires de chemins les plus courts dans l'arbre
Aug 28, 2023 pm 03:17 PM
Dans les arbres, le terme « somme des chemins les plus courts de toutes les paires de nœuds » fait référence au calcul de la somme des chemins les plus courts individuels de toutes les paires de nœuds. Une méthode efficace consiste à utiliser l’algorithme double DFS (profondeur d’abord recherche). La distance entre le nœud sélectionné et tous les autres nœuds est déterminée lors du premier passage DFS. L'arbre est parcouru à nouveau lors de la deuxième passe DFS, en considérant chaque nœud comme un LCA potentiel (ancêtre commun le plus bas) et en calculant la somme des distances entre les paires de nœuds descendants du LCA sélectionné. En utilisant cette méthode, vous pouvez calculer la somme des chemins les plus courts pour toutes les paires de nœuds de l'arborescence et garantir une solution idéale. Méthodes utilisées Méthode Dual DFS (Depth First Search) Méthode de programmation dynamique Méthode Dual DFS (Depth First Search) pour l'arborescence. Toutes les paires de chemins les plus courts
 Comment implémenter l'algorithme du chemin le plus court en utilisant Java
Sep 19, 2023 am 08:18 AM
Comment implémenter l'algorithme du chemin le plus court en utilisant Java
Sep 19, 2023 am 08:18 AM
Présentation de l'utilisation de Java pour implémenter l'algorithme du chemin le plus court : L'algorithme du chemin le plus court est une application importante dans la théorie des graphes et est largement utilisé dans le routage réseau, la navigation cartographique et d'autres domaines. Dans cet article, nous apprendrons comment implémenter l'algorithme du chemin le plus court à l'aide de Java et fournirons des exemples de code concrets. Idée d'algorithme : Il existe de nombreuses façons d'implémenter l'algorithme du chemin le plus court, parmi lesquels les deux algorithmes les plus connus sont l'algorithme de Dijkstra et l'algorithme A*. Nous nous concentrerons ici sur l'implémentation de l'algorithme de Dijkstra. La base de l'algorithme de Dijkstra
 La merveilleuse utilisation de la récursivité dans les structures de données C++ : implémentation de piles et d'arbres
May 04, 2024 pm 01:54 PM
La merveilleuse utilisation de la récursivité dans les structures de données C++ : implémentation de piles et d'arbres
May 04, 2024 pm 01:54 PM
Application de la récursion dans les structures de données C++ : Pile : La pile est implémentée de manière récursive via la structure dernier entré, premier sorti (LIFO). Arbre : L'arbre est implémenté de manière récursive via une structure hiérarchique, prenant en charge des opérations telles que l'insertion et le calcul de profondeur. La récursion fournit une solution concise et efficace pour traiter les structures imbriquées, rendant la mise en œuvre des structures de données plus intuitive et plus facile à maintenir.
 Exploration approfondie des méthodes d'application et d'implémentation des structures de données non linéaires des arbres et des graphiques en Java
Dec 26, 2023 am 10:22 AM
Exploration approfondie des méthodes d'application et d'implémentation des structures de données non linéaires des arbres et des graphiques en Java
Dec 26, 2023 am 10:22 AM
Comprendre les arbres et les graphiques en Java : exploration des applications et des implémentations de structures de données non linéaires Introduction En informatique, les structures de données sont la manière dont les données sont stockées, organisées et gérées dans les ordinateurs. Les structures de données peuvent être divisées en structures de données linéaires et structures de données non linéaires. Les arbres et les graphiques sont les deux types de structures de données non linéaires les plus couramment utilisés. Cet article se concentrera sur les concepts, les applications et l'implémentation des arbres et des graphiques en Java, et donnera des exemples de code spécifiques. Le concept et l'application de l'arbre Un arbre est un type de données abstrait, une collection de nœuds et d'arêtes. Chaque nœud de l'arbre contient un numéro
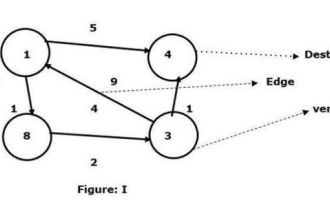 Trouvez le chemin le plus court entre deux nœuds à l'aide de l'algorithme Floyd-Warshal
Sep 20, 2023 pm 02:21 PM
Trouvez le chemin le plus court entre deux nœuds à l'aide de l'algorithme Floyd-Warshal
Sep 20, 2023 pm 02:21 PM
C++ a une macro, qui est définie comme un morceau de code ou une valeur attendue, et elle sera réutilisée chaque fois que l'utilisateur en aura besoin. L'algorithme de Floyd-Walshall est le processus permettant de trouver le chemin le plus court entre toutes les paires de sommets dans un graphe pondéré donné. L'algorithme suit une approche de programmation dynamique pour trouver le graphique de poids minimum. Comprenons la signification de l'algorithme de Floyd-Walshall à travers un diagramme - prenons le sommet 1 comme source et le sommet 4 comme destination et trouvons le chemin le plus court entre eux. Nous avons vu qu'il existe deux chemins qui peuvent être connectés au sommet cible 4. 1->4 – l'arête a un poids de 51->8->3->4 – le poids de l'arête (1+2+1) est 4. Dans le graphique I donné, nous voyons la plus petite arête reliant deux sommets. Voici donc le sommet
 Idées de conception d'algorithmes PHP : Comment parvenir à une solution efficace au problème du chemin le plus court des graphiques ?
Sep 19, 2023 pm 03:43 PM
Idées de conception d'algorithmes PHP : Comment parvenir à une solution efficace au problème du chemin le plus court des graphiques ?
Sep 19, 2023 pm 03:43 PM
Idées de conception d'algorithmes PHP : Comment parvenir à une solution efficace au problème du chemin le plus court des graphiques ? Dans le développement réel, nous devons souvent résoudre le problème du chemin le plus court, comme dans la navigation cartographique, le routage réseau, la distribution logistique et d'autres domaines. L’algorithme du plus court chemin pour les graphiques est la clé pour résoudre ce type de problème. Un graphe est constitué d'un ensemble de sommets et d'un ensemble d'arêtes. Les sommets représentent les nœuds et les arêtes représentent les relations entre les nœuds. Le problème du chemin le plus court consiste à trouver le chemin le plus court reliant deux nœuds. En PHP, nous pouvons utiliser une variété d’algorithmes pour résoudre le problème du chemin le plus court, dont le plus célèbre est
 Utilisez C++ pour supprimer tous les nœuds qui ne se trouvent sur aucun chemin et dont la somme du chemin est inférieure à k
Sep 04, 2023 am 10:17 AM
Utilisez C++ pour supprimer tous les nœuds qui ne se trouvent sur aucun chemin et dont la somme du chemin est inférieure à k
Sep 04, 2023 am 10:17 AM
Dans ce problème, nous avons un arbre binaire dont le chemin du nœud racine au nœud feuille est entièrement défini. La somme de tous les nœuds du nœud racine aux nœuds feuilles doit être supérieure ou égale à k. Nous devons donc supprimer tous les nœuds du chemin dont la somme est inférieure à k. La chose importante à retenir ici est qu'un nœud peut faire partie de plusieurs chemins, donc seulement si la somme de tous les chemins restants est 10+20+5, soit 25, soit moins de 150, nous devons l'élaguer et le supprimer. 5 . Après cela, évaluons 10->30->40. C'est moins de 150, alors supprimez 40. Maintenant nous voyons un autre chemin 10->20->35->50 et la somme 115 est inférieure à 150, donc
 Programme C++ pour supprimer les nœuds qui ne satisfont pas le chemin et qui sont supérieurs ou égaux à k
Sep 14, 2023 am 11:25 AM
Programme C++ pour supprimer les nœuds qui ne satisfont pas le chemin et qui sont supérieurs ou égaux à k
Sep 14, 2023 am 11:25 AM
Dans ce problème, nous avons un arbre binaire dont le chemin du nœud racine au nœud feuille est entièrement défini. La somme de tous les nœuds du nœud racine aux nœuds feuilles doit être supérieure ou égale à la valeur constante k. Par conséquent, nous devons supprimer tous les nœuds des chemins dont la somme est inférieure à k, de sorte que les chemins restants dans l’arborescence soient supérieurs à k. La chose importante à retenir ici est qu'un nœud peut faire partie de plusieurs chemins, donc seulement si la somme de tous les chemins menant à ce nœud, à gauche, totalise 10+20+5, soit 25, soit moins de 150, nous avons besoin pour couper et retirer 5. Après cela, évaluons 10->30->40. Il est inférieur à 150, donc 40 est supprimé. Maintenant nous voyons un autre chemin 10->20-





