Programme C pour trouver le changement

Dans ce problème, on nous donne une valeur n, nous voulons changer n roupies, et nous avons n pièces, chaque pièce a une valeur nominale allant de 1 à m. Nous devons renvoyer le nombre total de façons dont cette somme peut être formée. La traduction chinoise de
Example
Input : N = 6 ; coins = {1,2,4}.
Output : 6
Explanation : The total combination that make the sum of 6
is :
{1,1,1,1,1,1} ; {1,1,1,1,2}; {1,1,2,2}; {1,1,4}; {2,2,2} ; {2,4}.Example
est :Example
#include <stdio.h>
int coins( int S[], int m, int n ) {
int i, j, x, y;
int table[n+1][m];
for (i=0; i<m; i++)
table[0][i] = 1;
for (i = 1; i < n+1; i++) {
for (j = 0; j < m; j++) {
x = (i-S[j] >= 0)? table[i - S[j]][j]: 0;
y = (j >= 1)? table[i][j-1]: 0;
table[i][j] = x + y;
}
}
return table[n][m-1];
}
int main() {
int arr[] = {1, 2, 3};
int m = sizeof(arr)/sizeof(arr[0]);
int n = 4;
printf("The total number of combinations of coins that sum up to %d",n);
printf(" is %d ", coins(arr, m, n));
return 0;
}Output
The total number of combinations of coins that sum up to 4 is 4
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment implémenter un algorithme glouton en C#
Sep 19, 2023 am 11:48 AM
Comment implémenter un algorithme glouton en C#
Sep 19, 2023 am 11:48 AM
Comment implémenter l'algorithme glouton en C# L'algorithme glouton (algorithme Greedy) est une méthode de résolution de problèmes couramment utilisée. Il sélectionne à chaque fois la solution optimale actuelle dans l'espoir d'obtenir la solution optimale globale. En C#, nous pouvons utiliser des algorithmes gloutons pour résoudre de nombreux problèmes pratiques. Cet article présentera comment implémenter l'algorithme glouton en C# et fournira des exemples de code spécifiques. 1. Principes de base de l'algorithme glouton L'idée de base de l'algorithme glouton est de choisir à chaque fois la solution optimale actuelle, quel que soit l'impact possible des étapes ultérieures. Ce genre de pensée
 Comment implémenter une solution efficace au problème du moindre changement de pièce en PHP en utilisant l'algorithme glouton ?
Sep 19, 2023 am 10:22 AM
Comment implémenter une solution efficace au problème du moindre changement de pièce en PHP en utilisant l'algorithme glouton ?
Sep 19, 2023 am 10:22 AM
Comment implémenter une solution efficace au problème du moindre changement de pièce en PHP en utilisant l'algorithme glouton ? Introduction : Dans la vie quotidienne, nous avons souvent besoin d'apporter des changements, notamment lors de nos achats ou de nos échanges commerciaux. Pour utiliser le moins de pièces possible, le montant de la monnaie doit être combiné en utilisant le moins de pièces possible. En programmation informatique, nous pouvons utiliser un algorithme glouton pour résoudre ce problème afin d'obtenir une solution efficace. Cet article présentera comment utiliser l'algorithme glouton en PHP pour obtenir une solution efficace au problème de changement minimum de pièces et fournira des exemples de code correspondants.
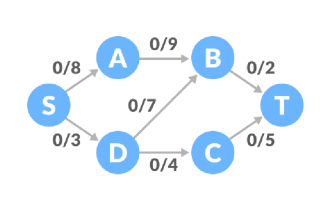 Analyser l'algorithme Ford-Fulkerson et l'implémenter via Python
Jan 22, 2024 pm 08:09 PM
Analyser l'algorithme Ford-Fulkerson et l'implémenter via Python
Jan 22, 2024 pm 08:09 PM
L'algorithme de Ford-Fulkerson est un algorithme glouton permettant de calculer le débit maximum dans un réseau. Le principe est de trouver un chemin augmentant avec une capacité restante positive. Tant que le chemin augmentant est trouvé, vous pouvez continuer à ajouter des chemins et à calculer le trafic. Jusqu'à ce que le chemin d'augmentation n'existe plus, le débit maximum peut être obtenu. Le terme capacité restante de l'algorithme de Ford-Fulkerson consiste à soustraire le flux de la capacité. Dans l'algorithme de Ford-Fulkerson, la capacité restante est un nombre positif avant de pouvoir continuer à être utilisée comme chemin. Réseau résiduel : C'est un réseau avec les mêmes sommets et arêtes, utilisant la capacité résiduelle comme capacité. Chemin augmenté : C'est le chemin du point source au point récepteur dans le graphe résiduel, avec une capacité finale de 0. Un aperçu possible de l'exemple de principe de l'algorithme de Ford-Fulkerson
 Comment implémenter un algorithme glouton en utilisant Python ?
Sep 19, 2023 am 11:43 AM
Comment implémenter un algorithme glouton en utilisant Python ?
Sep 19, 2023 am 11:43 AM
Comment implémenter un algorithme glouton en utilisant Python ? L'algorithme gourmand est un algorithme simple et efficace adapté à la résolution de problèmes avec des propriétés de sous-structure optimales. Il prend le meilleur choix dans l’état actuel à chaque étape de sélection, en espérant trouver la solution globale optimale. Dans cet article, nous présenterons comment utiliser Python pour implémenter l'algorithme glouton, avec des exemples de code spécifiques. 1. L'idée de base de l'algorithme glouton L'idée de base de l'algorithme glouton est de sélectionner la solution optimale dans l'état actuel à chaque étape, puis
 Comment écrire un algorithme glouton en utilisant PHP
Jul 07, 2023 pm 03:45 PM
Comment écrire un algorithme glouton en utilisant PHP
Jul 07, 2023 pm 03:45 PM
Comment utiliser PHP pour écrire un algorithme glouton L'algorithme gourmand (algorithme gourmand) est un algorithme simple et efficace utilisé pour résoudre un type de problème d'optimisation. Son idée fondamentale est de faire, à chaque étape, le choix qui semble le meilleur sur le moment, sans égard aux conséquences futures. Cet article expliquera comment écrire un algorithme glouton en utilisant PHP et fournira des exemples de code pertinents. 1. Description du problème Avant d'expliquer l'algorithme glouton, définissons d'abord un problème spécifique pour une meilleure compréhension. Supposons qu'il existe un ensemble de tâches, chaque tâche a un début
 Algorithme gourmand et son implémentation en C++
Aug 22, 2023 am 10:04 AM
Algorithme gourmand et son implémentation en C++
Aug 22, 2023 am 10:04 AM
L’algorithme glouton est une idée d’algorithme couramment utilisée et largement utilisée dans de nombreux problèmes. L’idée centrale est de considérer uniquement la solution optimale immédiate lors de la prise de décision à chaque étape, sans tenir compte de l’impact à long terme. En C++, la mise en œuvre d’algorithmes gloutons implique souvent des opérations de base telles que le tri et le traitement des données. Ci-dessous, nous présenterons l'idée d'un algorithme glouton et son implémentation en C++ pour plusieurs problèmes typiques. 1. Problème de planification des activités Étant donné un ensemble d'activités, chaque activité a son heure de début et son heure de fin, et une personne ne peut participer qu'à une seule activité à la fois.
 Implémentation d'un algorithme de division de récupération d'entiers non signés en C++
Sep 12, 2023 pm 04:01 PM
Implémentation d'un algorithme de division de récupération d'entiers non signés en C++
Sep 12, 2023 pm 04:01 PM
Discutez de la division d’entiers non signés à l’aide de l’algorithme de division. Certains algorithmes de division sont implémentés sur papier, d'autres sont implémentés sur des circuits numériques. Il existe deux algorithmes de division : l’algorithme de division lente et l’algorithme de division rapide. Les algorithmes de division lente comprennent les algorithmes de récupération, les algorithmes de récupération sans exécution, les algorithmes SRT et les algorithmes de non-récupération. Dans ce tutoriel, nous discuterons de l'algorithme de récupération en supposant que 0
 Comment implémenter un algorithme glouton en utilisant Java
Sep 19, 2023 am 11:13 AM
Comment implémenter un algorithme glouton en utilisant Java
Sep 19, 2023 am 11:13 AM
Comment utiliser Java pour implémenter un algorithme glouton L'algorithme glouton (GreedyAlgorithm) est une idée algorithmique pour résoudre des problèmes. Sa caractéristique est de sélectionner la solution optimale actuelle à chaque étape, dans l'espoir d'atteindre éventuellement la solution optimale globale à travers chaque solution optimale locale. Les caractéristiques simples et efficaces de l’algorithme glouton en font un algorithme couramment utilisé lors de la résolution de certains problèmes d’optimisation ou de certains problèmes spécifiques. Cet article présentera comment implémenter l'algorithme glouton à l'aide de Java et fournira des exemples de code spécifiques. 1. L'idée de base de l'algorithme glouton La base de l'algorithme glouton






