Somme des n premiers nombres naturels dans le programme C

Le concept de trouver la somme de la somme des entiers se trouve comme ceci, d'abord, nous trouverons la somme des nombres de 1 à n, puis additionnerons toutes les sommes et obtiendrons une valeur, cette valeur est quoi nous avons besoin et de et.
Pour ce problème, on nous donne un nombre n et nous voulons trouver la somme de somme, donnons un exemple pour trouver cette somme.
n = 4
Maintenant, nous allons trouver la somme des nombres pour chaque nombre de 1 à 4 :
Sum of numbers till 1 = 1 Sum of numbers till 2 = 1 + 2 = 3 Sum of numbers till 3 = 1 + 2 + 3 = 6 Sum of numbers till 4 = 1 + 2 + 3 + 4 = 10 Now we will find the sum of sum of numbers til n : Sum = 1+3+6+10 = 20
Pour trouver la somme des sommes de n nombres naturels, nous avons deux méthodes :
Méthode 1 - Utiliser la boucle for ( faible Efficace)
Méthode 2 - Utiliser une formule mathématique (Efficace)
Méthode 1 - Utiliser la boucle for
Dans cette méthode, nous utiliserons deux boucles for pour trouver la somme de la somme. La boucle interne trouve la somme des nombres naturels et la boucle externe ajoute cette somme à sum2 et incrémente le nombre de un.
Exemple
#include <stdio.h>
int main() {
int n = 4;
int sum=0, s=0;
for(int i = 1; i< n; i++){
for(int j= 1; j<i;j++ ){
s+= j;
}
sum += s;
}
printf("the sum of sum of natural number till %d is %d", n,sum);
return 0;
}Sortie
The sum of sum of natural number till 4 is 5
Méthode 2 - Utilisation d'une formule mathématique
Nous avons une formule mathématique pour trouver la somme de n nombres naturels. La méthode des formules mathématiques est une méthode efficace.
La formule mathématique pour résoudre la somme de n nombres naturels est :
sum = n*(n+1)*(n+2)/2
Exemple
La traduction chinoise est :Exemple
#include <stdio.h>
int main() {
int n = 4;
int sum = (n*(n+1)*(n+2))/2;
printf("the sum of sum of natural number till %d is %d", n,sum);
return 0;
}Sortie
the sum of sum of natural number till 4 is 60
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Traduisez ce qui suit en chinois : Programme C pour convertir des chiffres romains en nombres décimaux
Sep 05, 2023 pm 09:53 PM
Traduisez ce qui suit en chinois : Programme C pour convertir des chiffres romains en nombres décimaux
Sep 05, 2023 pm 09:53 PM
Vous trouverez ci-dessous un algorithme en langage C pour convertir les chiffres romains en nombres décimaux : Algorithme Étape 1 - Démarrer Étape 2 - Lire les chiffres romains au moment de l'exécution Étape 3 - Longueur : = strlen (roman) Étape 4 - Pour i = 0 à Longueur-1 Étape 4.1-switch(roman[i]) Étape 4.1.1-case'm' : &nbs
 Options de carte mère ASUS compatibles avec R55600 (y compris R55600u et 5600h)
Jan 02, 2024 pm 05:32 PM
Options de carte mère ASUS compatibles avec R55600 (y compris R55600u et 5600h)
Jan 02, 2024 pm 05:32 PM
Quelle carte mère ASUS faut-il associer au R55600 ? La carte mère ASUS ROGStrixB550-FGaming est un excellent choix. Il est parfaitement compatible avec le processeur Ryzen55600X et offre d'excellentes performances et fonctionnalités. Cette carte mère dispose d'un système d'alimentation fiable, peut prendre en charge l'overclocking et fournit une multitude d'emplacements et de ports d'extension pour répondre aux besoins quotidiens d'utilisation et de jeu. Le ROGStrixB550-FGaming est également équipé de solutions audio de haute qualité, de connexions réseau rapides et d'une conception de dissipation thermique fiable pour garantir que le système reste efficace et stable. De plus, cette carte mère adopte également le magnifique style ROG et est équipée de superbes effets d'éclairage RVB, ajoutant du plaisir visuel à votre ordinateur. Dans l’ensemble, ASUS ROGStri
 Programme C++ pour trouver la valeur de la fonction sinus hyperbolique inverse en prenant une valeur donnée comme argument
Sep 17, 2023 am 10:49 AM
Programme C++ pour trouver la valeur de la fonction sinus hyperbolique inverse en prenant une valeur donnée comme argument
Sep 17, 2023 am 10:49 AM
Les fonctions hyperboliques sont définies à l'aide d'hyperboles au lieu de cercles et sont équivalentes aux fonctions trigonométriques ordinaires. Il renvoie le paramètre de rapport dans la fonction sinus hyperbolique à partir de l'angle fourni en radians. Mais faites le contraire, ou en d’autres termes. Si nous voulons calculer un angle à partir d’un sinus hyperbolique, nous avons besoin d’une opération trigonométrique hyperbolique inverse comme l’opération sinus hyperbolique inverse. Ce cours montrera comment utiliser la fonction sinus hyperbolique inverse (asinh) en C++ pour calculer des angles en utilisant la valeur du sinus hyperbolique en radians. L'opération arc sinus hyperbolique suit la formule suivante -$$\mathrm{sinh^{-1}x\:=\:In(x\:+\:\sqrt{x^2\:+\:1})}, Où\:In\:is\:logarithme naturel\:(log_e\:k)
 Programme C pour trouver la longueur de la liste chaînée
Sep 07, 2023 pm 07:33 PM
Programme C pour trouver la longueur de la liste chaînée
Sep 07, 2023 pm 07:33 PM
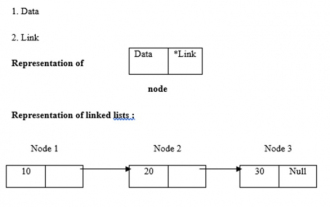
Les listes chaînées utilisent l’allocation dynamique de mémoire, c’est-à-dire qu’elles grandissent et diminuent en conséquence. Ils sont définis comme des collections de nœuds. Ici, un nœud comporte deux parties, des données et des liens. Les données, liens et listes chaînées sont représentés comme suit - Types de listes chaînées Il existe quatre types de listes chaînées, comme suit : - Liste chaînée simple / Liste chaînée simple Liste chaînée double / Double Liste chaînée simple circulaire Liste chaînée double circulaire Nous utilisons le méthode récursive pour trouver la longueur de la liste chaînée La logique est -intlength(node *temp){ if(temp==NULL) returnl{&n
 Lequel est le meilleur, Celeron g4900 ou i36100 ? (Lequel est le meilleur, Celeron g4900 ou i34170 ?)
Jan 01, 2024 pm 06:01 PM
Lequel est le meilleur, Celeron g4900 ou i36100 ? (Lequel est le meilleur, Celeron g4900 ou i34170 ?)
Jan 01, 2024 pm 06:01 PM
Lequel est le meilleur, Celeron g4900 ou i36100 ? En ce qui concerne les deux processeurs Celeron G4900 et I36100, il ne fait aucun doute que les performances du I36100 sont supérieures. Les processeurs Celeron sont généralement considérés comme des processeurs bas de gamme et sont principalement utilisés dans les ordinateurs portables économiques. Le processeur I3 est principalement utilisé pour les processeurs haut de gamme et ses performances sont très bonnes. Que vous jouiez à des jeux ou regardiez des vidéos, vous ne rencontrerez aucun décalage lors de l'utilisation du processeur I3. Par conséquent, si vous le pouvez, essayez d'acheter des processeurs Intel de la série I, en particulier pour les ordinateurs de bureau, afin de pouvoir profiter du plaisir du monde en ligne. Quelles sont les performances du Celeron G4900T ? Du point de vue des performances, le Pentium G4900T fonctionne bien en termes de fréquence. Par rapport à la version précédente, les performances du processeur sont.
 Programme C++ pour imprimer le dictionnaire
Sep 11, 2023 am 10:33 AM
Programme C++ pour imprimer le dictionnaire
Sep 11, 2023 am 10:33 AM
Une carte est un type spécial de conteneur en C++ où chaque élément est une paire de deux valeurs, à savoir une valeur clé et une valeur mappée. La valeur clé est utilisée pour indexer chaque élément et la valeur mappée est la valeur associée à la clé. Que la valeur mappée soit unique ou non, la clé est toujours unique. Pour imprimer des éléments de carte en C++, nous devons utiliser un itérateur. Un élément dans un ensemble d’éléments est indiqué par un objet itérateur. Les itérateurs sont principalement utilisés avec des tableaux et d'autres types de conteneurs (tels que des vecteurs), et ils disposent d'un ensemble spécifique d'opérations qui peuvent être utilisées pour identifier des éléments spécifiques dans une plage spécifique. Les itérateurs peuvent être incrémentés ou décrémentés pour référencer différents éléments présents dans une plage ou un conteneur. L'itérateur pointe vers l'emplacement mémoire d'un élément spécifique dans la plage. Imprimer une carte en C++ à l'aide d'itérateurs Voyons d'abord comment définir
 Carré moyen des nombres naturels ?
Sep 20, 2023 pm 10:29 PM
Carré moyen des nombres naturels ?
Sep 20, 2023 pm 10:29 PM
La moyenne des carrés des nombres naturels est calculée en additionnant tous les carrés de n nombres naturels puis en divisant par ce nombre. Les deux premiers nombres naturels de l'exemple sont 2,5, 12+22=5=>5/2=2,5. Il existe deux méthodes de calcul en programmation : Utiliser des boucles Utiliser des formules Calculer la moyenne des carrés de nombres naturels à l'aide de boucles Cette logique fonctionne en trouvant les carrés de tous les nombres naturels. Trouvez le carré de chacun en bouclant de 1 à n et ajoutez à la variable somme. Divisez ensuite cette somme par n. Programme pour calculer la somme des carrés de nombres naturels - exemple de code de démonstration en temps réel #include<stdio.h>intmain(){ intn=2;
 Le programme C utilise la fonction rename() pour changer le nom du fichier
Sep 21, 2023 pm 10:01 PM
Le programme C utilise la fonction rename() pour changer le nom du fichier
Sep 21, 2023 pm 10:01 PM
La fonction renommer modifie un fichier ou un répertoire de son ancien nom à son nouveau nom. Cette opération est similaire à l’opération de déplacement. Nous pouvons donc également utiliser cette fonction de renommage pour déplacer des fichiers. Cette fonction existe dans le fichier d'en-tête de la bibliothèque stdio.h. La syntaxe de la fonction rename est la suivante : intrename(constchar*oldname,constchar*newname); La fonction rename() accepte deux paramètres. L’un est l’ancien nom et l’autre le nouveau nom. Les deux paramètres sont des pointeurs vers des caractères constants qui définissent l'ancien et le nouveau nom du fichier. Renvoie zéro si le fichier a été renommé avec succès ; sinon, renvoie un entier différent de zéro. Lors d'une opération de changement de nom






