 développement back-end
développement back-end
 C++
C++
 Programmation en C++, trouver le nombre de chemins d'un point à un autre dans une grille
Programmation en C++, trouver le nombre de chemins d'un point à un autre dans une grille
Programmation en C++, trouver le nombre de chemins d'un point à un autre dans une grille

Dans cet article, on nous pose un problème dans lequel nous devons trouver le nombre total de chemins du point A au point B, où A et B sont des points fixes, c'est-à-dire A est le point du coin supérieur gauche de la grille et B est le point du coin inférieur droit de la grille, par exemple −
Input : N = 5 Output : 252 Input : N = 4 Output : 70 Input : N = 3 Output : 20
Dans le problème donné, nous pouvons formaliser la réponse et dériver le résultat à travers des observations simples.
Méthode pour trouver la solution
Dans cette méthode, nous dérivons une formule par observation selon laquelle lorsque nous traversons la grille de A à B, nous devons aller à droite n fois et descendre n fois, ce qui signifie que nous devons tout trouver combinaisons de chemins possibles, nous obtenons donc la formule de combinaison de (n+n) et n.
Exemple
#include<bits/stdc++.h>
using namespace std;
int fact(int n){ // factorial function
if(n <= 1)
return 1;
return n * fact(n-1);
}
int main() {
int n = 5; // given n
int answer = 0; // our answer
answer = fact(n+n); // finding factorial of 2*n
answer = answer / (fact(n) * fact(n)); // (2*n)! / (n! + n!)
cout << answer << "\n";
}Sortie
252
Explication du code ci-dessus
Dans ce code, nous calculons la formule combinée de 2*n à n, car nous savons que du point A au point B, nous avons besoin exactement de deux directions 2 *n opérations sur , c'est-à-dire qu'il y a n opérations dans un sens et n opérations dans l'autre sens, on trouve donc toutes les combinaisons possibles de ces opérations, c'est-à-dire (2*n)!/ (n! + n! ) . La complexité temporelle globale du programme donné est O(1), ce qui signifie que notre complexité ne dépend pas du n donné.
Conclusion
Dans cet article, nous avons abordé le problème de trouver le nombre d'itinéraires d'un point à un autre point dans une grille. Nous avons également appris un programme C++ pour ce problème et notre approche complète pour le résoudre. Nous pouvons écrire le même programme dans d'autres langages tels que C, Java, Python et d'autres langages. Nous espérons que cet article vous a été utile.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Annotation de cadre de délimitation redondant multi-grille pour une détection précise des objets
Jun 01, 2024 pm 09:46 PM
Annotation de cadre de délimitation redondant multi-grille pour une détection précise des objets
Jun 01, 2024 pm 09:46 PM
1. Introduction Actuellement, les principaux détecteurs d'objets sont des réseaux à deux étages ou à un étage basés sur le réseau de classificateurs de base réutilisé du Deep CNN. YOLOv3 est l'un de ces détecteurs à un étage de pointe bien connus qui reçoit une image d'entrée et la divise en une matrice de grille de taille égale. Les cellules de grille avec des centres cibles sont chargées de détecter des cibles spécifiques. Ce que je partage aujourd'hui est une nouvelle méthode mathématique qui alloue plusieurs grilles à chaque cible pour obtenir une prédiction précise et précise du cadre de délimitation. Les chercheurs ont également proposé une amélioration efficace des données par copier-coller hors ligne pour la détection des cibles. La méthode nouvellement proposée surpasse considérablement certains détecteurs d’objets de pointe actuels et promet de meilleures performances. 2. Le réseau de détection de cibles en arrière-plan est conçu pour utiliser
 Étapes pour configurer la grille de caméra sur iPhone
Mar 26, 2024 pm 07:21 PM
Étapes pour configurer la grille de caméra sur iPhone
Mar 26, 2024 pm 07:21 PM
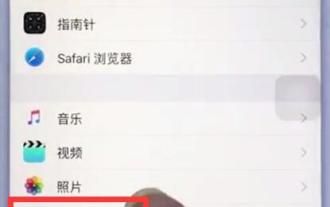
1. Ouvrez le bureau de votre iPhone, recherchez et cliquez pour accéder à [Paramètres], 2. Cliquez pour accéder à [Caméra] sur la page des paramètres. 3. Cliquez pour activer le commutateur sur le côté droit de [Grille].
 Conseils de mise en page CSS : meilleures pratiques pour la mise en œuvre de la disposition des icônes de grille circulaire
Oct 20, 2023 am 10:46 AM
Conseils de mise en page CSS : meilleures pratiques pour la mise en œuvre de la disposition des icônes de grille circulaire
Oct 20, 2023 am 10:46 AM
Conseils de mise en page CSS : meilleures pratiques pour la mise en œuvre de la mise en page des icônes de grille circulaire La mise en page en grille est une technique de mise en page courante et puissante dans la conception Web moderne. La disposition des icônes en grille circulaire est un choix de conception plus unique et plus intéressant. Cet article présente quelques bonnes pratiques et des exemples de code spécifiques pour vous aider à implémenter une disposition d'icônes de grille circulaire. Structure HTML Tout d'abord, nous devons configurer un élément conteneur et placer l'icône dans ce conteneur. Nous pouvons utiliser une liste non ordonnée (<ul>) comme conteneur, et les éléments de la liste (<l
 Écrit en C++, trouvez le nombre de triangles formés par un ensemble de points sur trois droites
Sep 09, 2023 am 09:53 AM
Écrit en C++, trouvez le nombre de triangles formés par un ensemble de points sur trois droites
Sep 09, 2023 am 09:53 AM
Maintenant, nous obtenons plusieurs points présents sur 3 lignes ; par exemple, nous devons savoir combien de triangles ces points peuvent former Input:m=3,n=4,k=5Output:205Input:m=2,n=2, k =1Sortie : 10 Nous appliquerons des mathématiques combinatoires pour résoudre ce problème et formulerons des formules pour résoudre ce problème. Méthode pour trouver une solution Dans cette méthode, nous élaborerons une formule : en appliquant la combinatoire à la situation actuelle, cette formule nous fournira le résultat. Code C++ pour la méthode ci-dessus Il s'agit d'une syntaxe C++ que nous pouvons utiliser comme entrée pour résoudre le problème donné - exemple #include<bits/stdc++.h>#define
 Comment taper le point '丶' à l'aide du clavier ?
Feb 15, 2024 pm 01:51 PM
Comment taper le point '丶' à l'aide du clavier ?
Feb 15, 2024 pm 01:51 PM
Lorsqu'ils tapent sur un clavier, de nombreux utilisateurs sont curieux de savoir comment taper le point « 丶 » sur le clavier ? Jetons donc un œil à la méthode que l'éditeur vous propose pour taper ce symbole « 丶 » sur le clavier. 1. Cliquez sur "丶" et tapez directement sur le clavier [dian]. Vous verrez le signe de ponctuation [丶] sur la barre de sélection. 2. Symboles spéciaux Dans la méthode de saisie Sogou Pinyin, lors du passage en mode chinois, appuyer sur la touche v fera apparaître des symboles spéciaux. Ces symboles incluent des nombres (par exemple : v123), des dates (par exemple : v2013/1/1), des calculs (par exemple : v1+1) et des fonctions (par exemple : v2~3). Ces symboles facilitent la saisie de diverses informations. 2. Appuyez ensuite à nouveau sur la touche numérique, n'importe quel nombre de 0 à 9 peut être utilisé
 Comment vérifier si trois points sont colinéaires en Java ?
Sep 05, 2023 pm 06:41 PM
Comment vérifier si trois points sont colinéaires en Java ?
Sep 05, 2023 pm 06:41 PM
Si trois points sont alignés, on dit qu’ils sont colinéaires. Si les points ne sont pas sur la même droite, ils ne sont pas colinéaires. Cela signifie que si trois points (x1,y1), (x2,y2), (x3,y3) sont sur la même droite, ils sont colinéaires. Parmi eux, x1, y1, x2, y2, x3, y3 sont des points sur l'axe des x et l'axe des y, (x1, y1), (x2, y2), (x3, y3) sont les coordonnées. Mathématiquement, il existe deux façons de déterminer si trois points sont colinéaires. Trouvez l'aire d'un triangle en utilisant les points. Si l'aire du triangle est nulle, alors les trois points sont colinéaires. Formule pour trouver une zone de triangle = 0,5*[x1*(y2-y3)+x2*
 Programmation en C++, trouver le nombre de chemins d'un point à un autre dans une grille
Aug 29, 2023 pm 10:25 PM
Programmation en C++, trouver le nombre de chemins d'un point à un autre dans une grille
Aug 29, 2023 pm 10:25 PM
Dans cet article, nous sommes confrontés à un problème dans lequel nous devons trouver le nombre total de chemins du point A au point B, où A et B sont des points fixes, c'est-à-dire A est le point du coin supérieur gauche de la grille et B est le point inférieur. point du coin droit, par exemple −Input:N=5Output:252Input:N=4Output:70Input:N=3Output:20 Dans le problème donné, nous pouvons formaliser la réponse et dériver le résultat à travers des observations simples. Méthode de recherche de solution Dans cette méthode, nous dérivons une formule en observant que lorsque nous traversons la grille de A à B, nous devons aller à droite n fois et descendre n fois, ce qui signifie que nous devons trouver toutes les combinaisons de chemins possibles, nous obtenons donc
 Programme C++ pour trouver le nombre de sauts requis par un robot pour atteindre une cellule spécifique dans une grille
Sep 17, 2023 pm 07:17 PM
Programme C++ pour trouver le nombre de sauts requis par un robot pour atteindre une cellule spécifique dans une grille
Sep 17, 2023 pm 07:17 PM
Disons que nous avons une grille hxw. La grille est représentée dans un tableau bidimensionnel appelé « initGrid », où chaque cellule de la grille est représentée par un « # » ou un « . ». '#' signifie qu'il y a un obstacle dans la grille, '.' signifie qu'il y a un chemin sur cette cellule. Maintenant, un robot est placé sur une cellule « c » de la grille qui a le numéro de ligne x et le numéro de colonne y. Le robot doit se déplacer d'une cellule « d » qui porte le numéro de ligne p et le numéro de colonne q vers une autre cellule. Les coordonnées de cellule c et d sont toutes deux données sous forme de paires d'entiers. Le robot peut désormais se déplacer d'une cellule à une autre comme suit : Si la cellule vers laquelle le robot souhaite se déplacer est située verticalement ou horizontalement à côté de la cellule actuelle, le robot peut





