
Dans ce problème, on nous donne un arbre binaire BT. Notre tâche est de trouver le plus grand sous-arbre de recherche binaire dans un arbre binaire donné.
L'arbre binaire est une structure de données spéciale utilisée pour le stockage de données. Les arbres binaires ont une condition spéciale selon laquelle chaque nœud peut avoir au plus deux nœuds enfants.
L'arbre de recherche binaire (BST) est un arbre qui satisfait aux propriétés suivantes :
La valeur clé du sous-arbre gauche est plus petite que la valeur clé de son nœud parent (nœud racine).
La valeur clé du sous-arbre droit est supérieure ou égale à la valeur clé de son nœud parent (nœud racine).
Prenons un exemple pour comprendre ce problème,
Entrée :
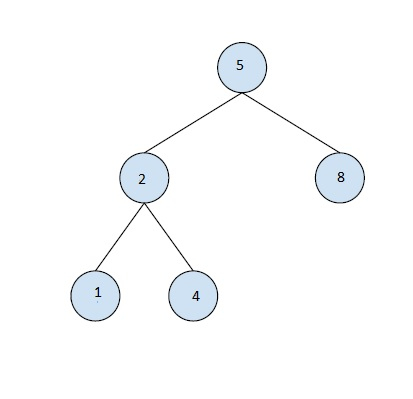
Sortie : 3
Explication
Full binary tree is a BST.
La façon simple de résoudre le problème est de faire le arbre en cours Parcours de la commande. Pour chaque nœud de l'arbre, vérifiez si son sous-arbre est un arbre de recherche binaire. Enfin, la taille du plus grand sous-arbre de recherche binaire est renvoyée.
Exemple de programme pour illustrer le fonctionnement de notre solution
#include<bits/stdc++.h>
using namespace std;
class node{
public:
int data;
node* left;
node* right;
node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
int findTreeSize(node* node) {
if (node == NULL)
return 0;
else
return(findTreeSize(node->left) + findTreeSize(node->right) + 1);
}
int isBSTree(struct node* node) {
if (node == NULL)
return 1;
if (node->left != NULL && node->left->data > node->data)
return 0;
if (node->right != NULL && node->right->data < node->data)
return 0;
if (!isBSTree(node->left) || !isBSTree(node->right))
return 0;
return 1;
}
int findlargestBSTSize(struct node *root) {
if (isBSTree(root)){
return findTreeSize(root);
}
else
return max(findlargestBSTSize(root->left), findlargestBSTSize(root->right));
}
int main() {
node *root = new node(5);
root->left = new node(2);
root->right = new node(8);
root->left->left = new node(1);
root->left->right = new node(4);
cout<<"The size of the largest possible BST is "<<findlargestBSTSize(root);
return 0;
}The size of the largest possible BST is 5
Une autre approche
Une autre façon de résoudre ce problème est de parcourir l'arbre depuis le bas et de vérifier à travers ses nœuds enfants s'il s'agit bien de BST. Pour ce faire, nous suivrons les éléments suivants : Si
est BST.
Dans le cas du sous-arbre de gauche, la valeur du plus grand élément.
Dans le cas du sous-arbre de droite, la valeur du plus petit élément. Ces valeurs doivent être comparées au nœud actuel pour vérifier le BST.
De plus, la taille du BST maximum sera mise à jour en la comparant avec la taille du BST actuel.
#include<bits/stdc++.h>
using namespace std;
class node{
public:
int data;
node* left;
node* right;
node(int data){
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
int findlargestBSTSizeRec(node* node, int *minValRsubTree, int *maxValLsubTree, int *maxBSTSize, bool *isBSTree) {
if (node == NULL){
*isBSTree = true;
return 0;
}
int min = INT_MAX;
bool left_flag = false;
bool right_flag = false;
int leftSubtreeSize,rightSubTreeSize;
*maxValLsubTree = INT_MIN;
leftSubtreeSize = findlargestBSTSizeRec(node->left, minValRsubTree, maxValLsubTree, maxBSTSize, isBSTree);
if (*isBSTree == true && node->data > *maxValLsubTree)
left_flag = true;
min = *minValRsubTree;
*minValRsubTree = INT_MAX;
rightSubTreeSize = findlargestBSTSizeRec(node->right, minValRsubTree, maxValLsubTree, maxBSTSize, isBSTree);
if (*isBSTree == true && node->data < *minValRsubTree)
right_flag = true;
if (min < *minValRsubTree)
*minValRsubTree = min;
if (node->data < *minValRsubTree)
*minValRsubTree = node->data;
if (node->data > *maxValLsubTree)
*maxValLsubTree = node->data;
if(left_flag && right_flag){
if (leftSubtreeSize + rightSubTreeSize + 1 > *maxBSTSize)
*maxBSTSize = (leftSubtreeSize + rightSubTreeSize + 1);
return (leftSubtreeSize + rightSubTreeSize + 1);
}
else{
*isBSTree = false;
return 0;
}
}
int findlargestBSTSize(node* node){
int min = INT_MAX;
int max = INT_MIN;
int largestBSTSize = 0;
bool isBST = false;
findlargestBSTSizeRec(node, &min, &max, &largestBSTSize, &isBST);
return largestBSTSize;
}
int main(){
node *root = new node(5);
root->left = new node(2);
root->right = new node(8);
root->left->left = new node(1);
root->left->right = new node(4);
cout<<"The Size of the largest BST is "<<findlargestBSTSize(root);
return 0;
}The Size of the largest BST is 5
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Que faire si la connexion win8wifi n'est pas disponible
Que faire si la connexion win8wifi n'est pas disponible
 Quel format de fichier est csv ?
Quel format de fichier est csv ?
 tutoriel CSS3
tutoriel CSS3
 Comment résoudre le statut http 404
Comment résoudre le statut http 404
 Comment ignorer la connexion à Internet après le démarrage de Windows 11
Comment ignorer la connexion à Internet après le démarrage de Windows 11
 Que signifie bloquer tous les cookies ?
Que signifie bloquer tous les cookies ?
 appuyez sur n'importe quelle touche pour redémarrer
appuyez sur n'importe quelle touche pour redémarrer
 ORACLEDISTINCT
ORACLEDISTINCT